Homework 4: B-Trees
CS186: Introduction to Database Systems
UC Berkeley
November 8, 2003
Due: November 18, 2003, at 8PM PST
Note: this will be an indivual project, not a group project!
1 Introduction
The operation of B-Trees is an important aspect of database systems; virtually every commercial system includes indexes based on B-Trees. In the past, cs186 has included a B-Tree assignment that involved implementing a B-Tree index for the Minibase database system. Creating such an index was technically quite difficult, since the index needed to be stored in pages on disk that were moved into memory when used. Luckily, your task will be considerably simpler: implementing the "search", "insert" and "delete" functions for an in-memory B-Tree that uses Integer keys.2 B-Trees
The structure and behavior of B-Trees is described in Chapter 10 of the textbook, and also in the lecture notes for Lecture 17, which covered tree-structured indexes. The textbook even includes a pseudo-code describing the process of search, insert, and delete. I recommend that you review these materials to make sure you understand how these operations work.3 The B-Tree Program
In class I demonstrated a B-Tree program I wrote in Java. The UI
appeared as follows: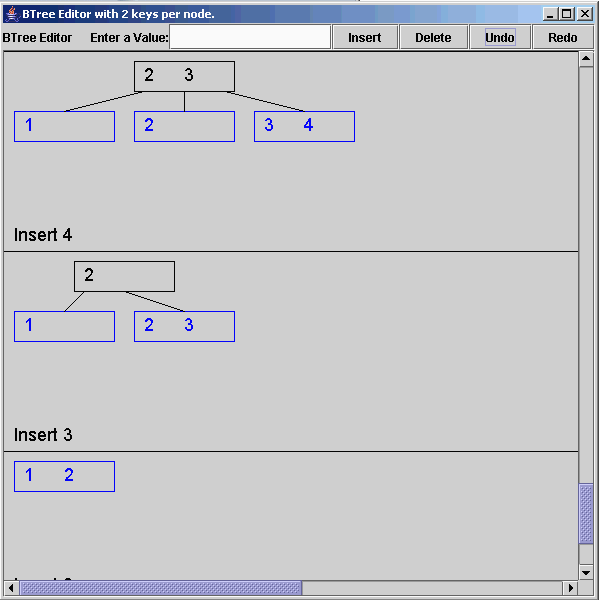
This program begins with an empty B-Tree, and allows the user to add and delete values. It also keeps track of the tree at each stage, so the user can see how the tree changes with insertion and deletion. In the tree display, leaf nodes are drawn blue, and the non-leaves as black. When started from the command line, this program accepts an integer argument indicating the maximum number of keys permitted per node. In the example above, nodes may have no more than two keys per node.
4 The Assignment
For this assignment, I will provide you with a Java .jar file Btree.jar containing most of the classes required to run the above program. All that will be missing is the Node class, in which is implemented logic for search, insertion, and deletion. The Node class is a subclass of AbstractNode, which contains members for keeping track of the keys and children for each node. A javadoc description of AbstractNode is available here. I am also providing sample java code for Node.java containing stubbed out versions of the search, insert, and delete methods.All the necessary files may be found in ~cs186/fa03/Hw4/Hw4.tar.gz. Copy this file and untar it in an appropriate directory. 'cd' to this directory. You can compile the Node.java file with the following command:
javac -classpath
".:./BTree.jar:$CLASSPATH" Node.java
Once you have compiled Node.java, you can run the program with the
following command:java -classpath
".:./BTree.jar:$CLASSPATH" BTreeMain 3
To run the above program allowing 3 keys per node.
5 Implementation Details
For search and insert, you should be able to follow the algorithms as described in the text book.For insert, do not do any redistribution of keys. When a node gets too full, just split it. As described in the book, when leaves split, you copy a key up, and when non-leaves split, push a key up.
For delete, in order to be consistent with the grading standard, you must follow the following
- after deletion, if a node has too few keys, always try redistribute keys from
the sibling to the left. If there is no sibling to the left, use
the sibling to the right. If there are not enough keys to
redistribute, then merge the two. For example, if I delete the
key "1" from the following tree (which permits only 2 keys per node):
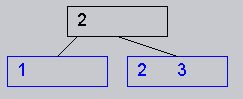
it should redistribute the key "2" from the right child to the left child, since there are enough keys in this. Remember, the default behavior is to try to redistribute keys from a sibling to the left, if any. In the above case, there is no sibling to the left, so the sibling to the right was used. And by definition, every node in the tree has at least one sibling.
- when redistributing keys from a sibling, always only redistribute
one key. The book talks about redistributing the keys evenly
between the two nodes, but I want you to only redistribute one
key.
For example, in the following tree (which allows 4 keys per node),
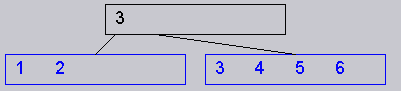
if I delete key "2" , it should redistribute only one key, key "3" from the right to the left.
I am providing code that should work properly with Java 1.2, 1.3, or 1.4. You probably will be able to work on the assignment on any machine running java. Your code will be compiled and tested on Pentagon, however, so you must make sure that it works correctly there.
6 How to test your program
Your code must be general enough to work with any number of keys per node (greater than one, of course). You should test your program with different numbers of keys per node. Make sure that your code correctly handles insertions that cause splits at any level of the tree, as well as deletions that cause redistribution from right sibling to left sibling, left sibling to right sibling, or sibling merges. Make sure you check each of these for both leaf cases and non-leaf cases.The program framework should help your debugging, since you can see the state of the tree after each step. In addition, the "Undo" and "Redo" buttons allow you to run an operation again, which is useful if you are running in a debugger and want to set breakpoints.