1.1.1   Programming in Python

A language isn't something you learn so much as something you join.

—Arika Okrent

In order to define computational processes, we need a programming language; preferably one that many humans and a great variety of computers can all understand. In this text, we will work primarily with the Python language.

Python is a widely used programming language that has recruited enthusiasts from many professions: web programmers, game engineers, scientists, academics, and even designers of new programming languages. When you learn Python, you join a million-person-strong community of developers. Developer communities are tremendously important institutions: members help each other solve problems, share their projects and experiences, and collectively develop software and tools. Dedicated members often achieve celebrity and widespread esteem for their contributions. Someday you may be named among the elite Pythonistas of the world.

The Python language itself is the product of a large volunteer community that prides itself on the diversity of its contributors. The language was conceived and first implemented by Guido van Rossum in the late 1980's. The first chapter of his Python 3 Tutorial explains why Python is so popular, among the many languages available today.

Python excels as an instructional language because, throughout its history, Python's developers have emphasized the human interpretability of Python code, reinforced by the Zen of Python guiding principles of beauty, simplicity, and readability. Python is particularly appropriate for this text because its broad set of features support a variety of different programming styles, which we will explore. While there is no single way to program in Python, there are a set of conventions shared across the developer community that facilitate reading, understanding, and extending existing programs. Hence, Python's combination of great flexibility and accessibility allows students to explore many programming paradigms, and then apply their newly acquired knowledge to thousands of ongoing projects.

These notes maintain the spirit of SICP by introducing the features of Python in lock step with techniques for abstraction design and a rigorous model of computation. In addition, these notes provide a practical introduction to Python programming, including some advanced language features and illustrative examples. Learning Python will come naturally as you progress through the text.

The best way to get started programming in Python is to interact with the interpreter directly. This section describes how to install Python 3, initiate an interactive session with the interpreter, and start programming.

1.1.2   Installing Python 3

As with all great software, Python has many versions. This text will use the most recent stable version of Python 3. Many computers have older versions of Python installed already, such as Python 2.6, but those will not match the descriptions in this text. You should be able to use any computer, but expect to install Python 3. Don't worry, Python is free.

The free online book Dive Into Python 3 has detailed installation instructions for all major platforms. These instructions mention Python 3.1 several times, but you're better off with the latest version of Python 3 (although the differences are insignificant for this text).

1.1.3   Interactive Sessions

In an interactive Python session, you type some Python code after the prompt, >>>. The Python interpreter reads and executes what you type, carrying out your various commands.

To start an interactive session, run the Python 3 application. Type python3 at a terminal prompt (Mac/Unix/Linux) or open the Python 3 application in Windows.

If you see the Python prompt, >>>, then you have successfully started an interactive session. These notes depict example interactions using the prompt, followed by some input.

>>> 2 + 2
4

Interactive controls. Each session keeps a history of what you have typed. To access that history, press <Control>-P (previous) and <Control>-N (next). <Control>-D exits a session, which discards this history. Up and down arrows also cycle through history on some systems.

1.1.4   First Example

And, as imagination bodies forth

The forms of things to unknown, and the poet's pen

Turns them to shapes, and gives to airy nothing

A local habitation and a name.

—William Shakespeare, A Midsummer-Night's Dream

To give Python a proper introduction, we will begin with an example that uses several language features. In the next section, we will start from scratch and build up the language piece by piece. Think of this section as a sneak preview of features to come.

Python has built-in support for a wide range of common programming activities, such as manipulating text, displaying graphics, and communicating over the Internet. The line of Python code

>>> from urllib.request import urlopen

is an import statement that loads functionality for accessing data on the Internet. In particular, it makes available a function called urlopen, which can access the content at a uniform resource locator (URL), which is a location of something on the Internet.

Statements & Expressions. Python code consists of expressions and statements. Broadly, computer programs consist of instructions to either

1. Compute some value
2. Carry out some action

Statements typically describe actions. When the Python interpreter executes a statement, it carries out the corresponding action. On the other hand, expressions typically describe computations. When Python evaluates an expression, it computes the value of that expression. This chapter introduces several types of statements and expressions.

The assignment statement

>>> shakespeare = urlopen('http://inst.eecs.berkeley.edu/~cs61a/fa11/shakespeare.txt')

associates the name shakespeare with the value of the expression that follows =. That expression applies the urlopen function to a URL that contains the complete text of William Shakespeare's 37 plays, all in a single text document.

Functions. Functions encapsulate logic that manipulates data. urlopen is a function. A web address is a piece of data, and the text of Shakespeare's plays is another. The process by which the former leads to the latter may be complex, but we can apply that process using only a simple expression because that complexity is tucked away within a function. Functions are the primary topic of this chapter.

Another assignment statement

>>> words = set(shakespeare.read().decode().split())

associates the name words to the set of all unique words that appear in Shakespeare's plays, all 33,721 of them. The chain of commands to read, decode, and split, each operate on an intermediate computational entity: we read the data from the opened URL, then decode the data into text, and finally split the text into words. All of those words are placed in a set.

Objects. A set is a type of object, one that supports set operations like computing intersections and membership. An object seamlessly bundles together data and the logic that manipulates that data, in a way that manages the complexity of both. Objects are the primary topic of Chapter 2. Finally, the expression

>>> {w for w in words if len(w) == 6 and w[::-1] in words}
{'redder', 'drawer', 'reward', 'diaper', 'repaid'}

is a compound expression that evaluates to the set of all Shakespearian words that are simultaneously a word spelled in reverse. The cryptic notation w[::-1] enumerates each letter in a word, but the -1 dictates to step backwards. When you enter an expression in an interactive session, Python prints its value on the following line.

Interpreters. Evaluating compound expressions requires a precise procedure that interprets code in a predictable way. A program that implements such a procedure, evaluating compound expressions, is called an interpreter. The design and implementation of interpreters is the primary topic of Chapter 3.

When compared with other computer programs, interpreters for programming languages are unique in their generality. Python was not designed with Shakespeare in mind. However, its great flexibility allowed us to process a large amount of text with only a few statements and expressions.

In the end, we will find that all of these core concepts are closely related: functions are objects, objects are functions, and interpreters are instances of both. However, developing a clear understanding of each of these concepts and their role in organizing code is critical to mastering the art of programming.

1.1.5   Practical Guidance: Errors

Python is waiting for your command. You are encouraged to experiment with the language, even though you may not yet know its full vocabulary and structure. However, be prepared for errors. While computers are tremendously fast and flexible, they are also extremely rigid. The nature of computers is described in Stanford's introductory course as

The fundamental equation of computers is: computer = powerful + stupid

Computers are very powerful, looking at volumes of data very quickly. Computers can perform billions of operations per second, where each operation is pretty simple.

Computers are also shockingly stupid and fragile. The operations that they can do are extremely rigid, simple, and mechanical. The computer lacks anything like real insight ... it's nothing like the HAL 9000 from the movies. If nothing else, you should not be intimidated by the computer as if it's some sort of brain. It's very mechanical underneath it all.

Programming is about a person using their real insight to build something useful, constructed out of these teeny, simple little operations that the computer can do.

—Francisco Cai and Nick Parlante, Stanford CS101

The rigidity of computers will immediately become apparent as you experiment with the Python interpreter: even the smallest spelling and formatting changes will cause unexpected output and errors.

Learning to interpret errors and diagnose the cause of unexpected errors is called debugging. Some guiding principles of debugging are:

1. Test incrementally: Every well-written program is composed of small, modular components that can be tested individually. Try out everything you write as soon as possible to identify problems early and gain confidence in your components.
2. Isolate errors: An error in the output of a statement can typically be attributed to a particular modular component. When trying to diagnose a problem, trace the error to the smallest fragment of code you can before trying to correct it.
3. Check your assumptions: Interpreters do carry out your instructions to the letter --- no more and no less. Their output is unexpected when the behavior of some code does not match what the programmer believes (or assumes) that behavior to be. Know your assumptions, then focus your debugging effort on verifying that your assumptions actually hold.
4. Consult others: You are not alone! If you don't understand an error message, ask a friend, instructor, or search engine. If you have isolated an error, but can't figure out how to correct it, ask someone else to take a look. A lot of valuable programming knowledge is shared in the process of group problem solving.

Incremental testing, modular design, precise assumptions, and teamwork are themes that persist throughout this text. Hopefully, they will also persist throughout your computer science career.

1.2.1   Expressions

Having experimented with the full Python interpreter in the previous section, we now start anew, methodically developing the Python language element by element. Be patient if the examples seem simplistic --- more exciting material is soon to come.

We begin with primitive expressions. One kind of primitive expression is a number. More precisely, the expression that you type consists of the numerals that represent the number in base 10.

>>> 42
42

Expressions representing numbers may be combined with mathematical operators to form a compound expression, which the interpreter will evaluate:

>>> -1 - -1
0
>>> 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
0.9921875

These mathematical expressions use infix notation, where the operator (e.g., +, -, *, or /) appears in between the operands (numbers). Python includes many ways to form compound expressions. Rather than attempt to enumerate them all immediately, we will introduce new expression forms as we go, along with the language features that they support.

Strings expressions. A string is a sequence of characters enclosed by matching single or double quotes, such as 'Python' and " is cool!". (The Python interpreter uses single quotes to represent a string, regardless of what kind of quote you use.)

>>> 'Python'
'Python'
>>> " is cool!"
' is cool!'

The enclosing quotes are not actually part of a string; they are merely used for representation. We can see that this is the case by using the + operator to concatenate multiple strings into a larger string:

>>> 'Python' + " is cool!"
'Python is cool!'

Strings are a general representation for any kind of text, such as words, phrases, URLs, error messages, and so on. Later, we will see many different ways to use and manipulate strings in Python.

1.2.2   Call Expressions

The most important kind of compound expression is a call expression, which applies a function to some arguments. Recall from algebra that the mathematical notion of a function is a mapping from some input arguments to an output value. For instance, the max function maps its inputs to a single output, which is the largest of the inputs. The way in which Python expresses function application is the same as in conventional mathematics.

>>> max(7.5, 9.5)
9.5

This call expression has subexpressions: the operator is an expression that precedes parentheses, which enclose a comma-delimited list of operand expressions.

The operator specifies a function. When this call expression is evaluated, we say that the function max is called with arguments 7.5 and 9.5, and returns a value of 9.5.

The order of the arguments in a call expression matters. For instance, the function pow raises its first argument to the power of its second argument.

>>> pow(100, 2)
10000
>>> pow(2, 100)
1267650600228229401496703205376

Function notation has three principal advantages over the mathematical convention of infix notation. First, functions may take an arbitrary number of arguments:

>>> max(1, -2, 3, -4)
3

No ambiguity can arise, because the function name always precedes its arguments.

Second, function notation extends in a straightforward way to nested expressions, where the elements are themselves compound expressions. In nested call expressions, unlike compound infix expressions, the structure of the nesting is entirely explicit in the parentheses.

>>> max(min(1, -2), min(pow(3, 5), -4))
-2

There is no limit (in principle) to the depth of such nesting and to the overall complexity of the expressions that the Python interpreter can evaluate. However, humans quickly get confused by multi-level nesting. An important role for you as a programmer is to structure expressions so that they remain interpretable by yourself, your programming partners, and other people who may read your expressions in the future.

Third, mathematical notation has a great variety of forms: multiplication appears between terms, exponents appear as superscripts, division as a horizontal bar, and a square root as a roof with slanted siding. Some of this notation is very hard to type! However, all of this complexity can be unified via the notation of call expressions. While Python supports common mathematical operators using infix notation (like + and -), any operator can be expressed as a function with a name.

1.2.3   Importing Library Functions

Python defines a very large number of functions, including the operator functions mentioned in the preceding section, but does not make all of their names available by default. Instead, it organizes the functions and other quantities that it knows about into modules, which together comprise the Python Library. To use these elements, one imports them. For example, the math module provides a variety of familiar mathematical functions:

>>> from math import sqrt
>>> sqrt(256)
16.0

and the operator module provides access to functions corresponding to infix operators:

>>> from operator import add, sub, mul
>>> add(14, 28)
42
>>> sub(100, mul(7, add(8, 4)))
16

An import statement designates a module name (e.g., operator or math), and then lists the named attributes of that module to import (e.g., sqrt). Once a function is imported, it can be called multiple times.

There is no difference between using these operator functions (e.g., add) and the operator symbols themselves (e.g., +). Conventionally, most programmers use symbols and infix notation to express simple arithmetic.

The Python 3 Library Docs list the functions defined by each module, such as the math module. However, this documentation is written for developers who know the whole language well. For now, you may find that experimenting with a function tells you more about its behavior than reading the documemtation. As you become familiar with the Python language and vocabulary, this documentation will become a valuable reference source.

1.2.4   Names and the Environment

A critical aspect of a programming language is the means it provides for using names to refer to computational objects. If a value has been given a name, we say that the name binds to the value.

In Python, we can establish new bindings using the assignment statement, which contains a name to the left of = and a value to the right:

>>> radius = 10
>>> radius
10
>>> 2 * radius
20

Names are also bound via import statements.

>>> from math import pi
>>> pi * 71 / 223
1.0002380197528042

The = symbol is called the assignment operator in Python (and many other languages). Assignment is our simplest means of abstraction, for it allows us to use simple names to refer to the results of compound operations, such as the area computed above. In this way, complex programs are constructed by building, step by step, computational objects of increasing complexity.

The possibility of binding names to values and later retrieving those values by name means that the interpreter must maintain some sort of memory that keeps track of the names, values, and bindings. This memory is called an environment.

Names can also be bound to functions. For instance, the name max is bound to the max function we have been using. Functions, unlike numbers, are tricky to render as text, so Python prints an identifying description instead, when asked to describe a function:

>>> max
<built-in function max>

We can use assignment statements to give new names to existing functions.

>>> f = max
>>> f
<built-in function max>
>>> f(2, 3, 4)
4

And successive assignment statements can rebind a name to a new value.

>>> f = 2
>>> f
2

In Python, names are often called variable names or variables because they can be bound to different values in the course of executing a program. When a name is bound to a new value through assignment, it is no longer bound to any previous value. One can even bind built-in names to new values.

>>> max = 5
>>> max
5

After assigning max to 5, the name max is no longer bound to a function, and so attempting to call max(2, 3, 4) will cause an error.

When executing an assignment statement, Python evaluates the expression to the right of = before changing the binding to the name on the left. Therefore, one can refer to a name in right-side expression, even if it is the name to be bound by the assignment statement.

>>> x = 2
>>> x = x + 1
>>> x
3

We can also assign multiple values to multiple names in a single statement, where names (on the left of =) and expressions (on the right of =) are separated by commas.

>>> area, circumference = pi * radius * radius, 2 * pi * radius
>>> area
314.1592653589793
>>> circumference
62.83185307179586

Changing the value of one name does not affect other names. Below, even though the name area was bound to a value defined originally in terms of radius, the value of area has not changed. Updating the value of area requires another assignment statement.

>>> radius = 11
>>> area
314.1592653589793
>>> area = pi * radius * radius
380.132711084365

With multiple assignment, all expressions to the left of = are evaluated before any names are bound to those values. As a result of this rule, swapping the values bound to two names can be performed in a single statement.

>>> x, y = 3, 4.5
>>> y, x = x, y
>>> x
4.5
>>> y
3

1.2.5   Evaluating Nested Expressions

One of our goals in this chapter is to isolate issues about thinking procedurally. As a case in point, let us consider that, in evaluating nested call expressions, the interpreter is itself following a procedure.

To evaluate a call expression, Python will do the following:

1. Evaluate the operator and operand subexpressions, then
2. Apply the function that is the value of the operator subexpression to the arguments that are the values of the operand subexpressions.

Even this simple procedure illustrates some important points about processes in general. The first step dictates that in order to accomplish the evaluation process for a call expression we must first evaluate other expressions. Thus, the evaluation procedure is recursive in nature; that is, it includes, as one of its steps, the need to invoke the rule itself.

For example, evaluating

>>> mul(add(2, mul(4, 6)), add(3, 5))
208

requires that this evaluation procedure be applied four times. If we draw each expression that we evaluate, we can visualize the hierarchical structure of this process.

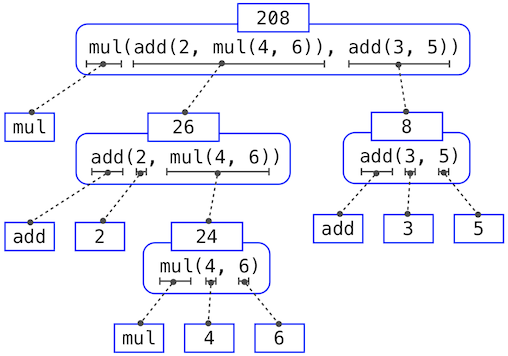
This illustration is called an expression tree. In computer science, trees conventionally grow from the top down. The objects at each point in a tree are called nodes; in this case, they are expressions paired with their values.

Evaluating its root, the full expression at the top, requires first evaluating the branches that are its subexpressions. The leaf expressions (that is, nodes with no branches stemming from them) represent either functions or numbers. The interior nodes have two parts: the call expression to which our evaluation rule is applied, and the result of that expression. Viewing evaluation in terms of this tree, we can imagine that the values of the operands percolate upward, starting from the terminal nodes and then combining at higher and higher levels.

Next, observe that the repeated application of the first step brings us to the point where we need to evaluate, not call expressions, but primitive expressions such as numerals (e.g., 2) and names (e.g., add). We take care of the primitive cases by stipulating that

• A numeral evaluates to the number it names,
• A name evaluates to the value associated with that name in the current environment.

Notice the important role of an environment in determining the meaning of the symbols in expressions. In Python, it is meaningless to speak of the value of an expression such as

>>> add(x, 1)

without specifying any information about the environment that would provide a meaning for the name x (or even for the name add). Environments provide the context in which evaluation takes place, which plays an important role in our understanding of program execution.

This evaluation procedure does not suffice to evaluate all Python code, only call expressions, numerals, and names. For instance, it does not handle assignment statements. Executing

>>> x = 3

does not return a value nor evaluate a function on some arguments, since the purpose of assignment is instead to bind a name to a value. In general, statements are not evaluated but executed; they do not produce a value but instead make some change. Each type of expression or statement has its own evaluation or execution procedure.

A pedantic note: when we say that "a numeral evaluates to a number," we actually mean that the Python interpreter evaluates a numeral to a number. It is the interpreter which endows meaning to the programming language. Given that the interpreter is a fixed program that always behaves consistently, we can loosely say that numerals (and expressions) themselves evaluate to values in the context of Python programs.

1.2.6   Types of Functions

Throughout this text, we will distinguish between two types of functions.

Pure functions. Functions have some input (their arguments) and return some output (the result of applying them). The built-in function

>>> abs(-2)
2

can be depicted as a small machine that takes input and produces output.

The function abs is pure. Pure functions have the property that applying them has no effects beyond returning a value. Moreover, a pure function must always return the same value when called twice with the same arguments.

Non-pure functions. In addition to returning a value, applying a non-pure function can generate side effects, which make some change to the state of the interpreter or computer. A common side effect is to generate additional output beyond the return value, using the print function.

>>> print(1, 2, 3)
1 2 3

While print and abs may appear to be similar in these examples, they work in fundamentally different ways. The value that print returns is always None, a special Python value that represents nothing. The interactive Python interpreter does not automatically print the value None. In the case of print, the function itself is printing output as a side effect of being called.

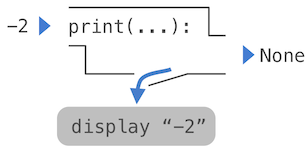
A nested expression of calls to print highlights the non-pure character of the function.

>>> print(print(1), print(2))
1
2
None None

If you find this output to be unexpected, draw an expression tree to clarify why evaluating this expression produces this peculiar output.

Be careful with print! The fact that it returns None means that it should not be the expression in an assignment statement.

>>> two = print(2)
2
>>> print(two)
None

Pure functions are restricted in that they cannot have side effects or change behavior over time. Imposing these restrictions yields substantial benefits. First, pure functions can be composed more reliably into compound call expressions. We can see in the non-pure function example above that print does not return a useful result when used in an operand expression. On the other hand, we have seen that functions such as max, pow and sqrt can be used effectively in nested expressions.

Second, pure functions tend to be simpler to test. A list of arguments will always lead to the same return value, which can be compared to the expected return value. Testing is discussed in more detail later in this chapter.

Third, Chapter 4 will illustrate that pure functions are essential for writing concurrent programs, in which multiple call expressions may be evaluated simultaneously.

For these reasons, we concentrate heavily on creating and using pure functions in the remainder of this chapter.

1.3.1   Environments

Our subset of Python is now complex enough that the meaning of programs is non-obvious. What if a formal parameter has the same name as a built-in function? Can two functions share names without confusion? To resolve such questions, we must describe environments in more detail.

An environment in which an expression is evaluated consists of a sequence of frames, depicted as boxes. Each frame contains bindings, each of which associates a name with its corresponding value. There is a single global frame. Assignment and import statements add entries to the first frame of the current environment. So far, our environment consists only of the global frame.

This environment diagram shows the bindings of the current environment, along with the values to which names are bound. The environment diagrams in this text are interactive: you can step through the lines of the small program on the left to see the state of the environment evolve on the right. You can also click on the "Edit code" link to load the example into the Online Python Tutor, a tool created by Philip Guo for generating these environment diagrams. You are encouraged to create examples yourself and study the resulting environment diagrams.

A def statement also binds a name to the function created by the definition. The resulting environment after defining square appears below:

Notice that the name of a function is repeated, once in the global frame, and once as part of the function itself.

This repetition is intentional: many different names may refer to the same function, but that function itself has only one intrinsic name. However, looking up the value for a name in an environment only inspects bound names. The intrinsic name of a function does not play a role in look up. In the example we saw earlier,

The name max is the intrinsic name of the function, and that's what you see printed as the value for f. In addition, both the names max and f are bound to that same function in the global environment.

Function Signatures. Functions differ in the number of arguments that they are allowed to take. To track these requirements, we draw each function in a way that shows the function name and its formal parameters. The user-defined function square takes only x; providing more or fewer arguments will result in an error. A description of the formal parameters of a function is called the function's signature.

The function max can take an arbitrary number of arguments. It is rendered as max(...). Regardless of the number of arguments taken, all built-in functions will be rendered as <name>(...), because these primitive functions were never explicitly defined.

1.3.2   Calling User-Defined Functions

To evaluate a call expression whose operator names a user-defined function, the Python interpreter follows a computational process. As with any call expression, the interpreter evaluates the operator and operand expressions, and then applies the named function to the resulting arguments.

Applying a user-defined function introduces a second local frame, which is only accessible to that function. To apply a user-defined function to some arguments:

1. Bind the arguments to the names of the function's formal parameters in a new local frame.
2. Execute the body of the function in the environment that starts with this frame.

The environment in which the body is evaluated consists of two frames: first the local frame that contains formal parameter bindings, then the global frame that contains everything else. Each instance of a function application has its own independent local frame.

To illustrate an example in detail, several steps of the environment diagram for the same example are depicted below. After executing the first import statement, only the name mul is bound in the global frame.

First, the definition statement for the function square is executed. Notice that the entire def statement is processed in a single step. The body of a function is not executed until the function is called (not when it is defined).

Next, The square function is called with the argument -2, and so a new frame is created with the formal parameter x bound to the value -2.

Then, the name x is looked up in the current environment, which consists of the two frames shown. In both occurrences, x evaluates to -2, and so the square function returns 4.

The "Return value" in the square() frame is not a name binding; instead it indicates the value returned by the function call that created the frame.

Even in this simple example, two different environments are used. The top-level expression square(-2) is evaluated in the global environment, while the return expression mul(x, x) is evaluated in the environment created for by calling square. Both x and mul are bound in this environment, but in different frames.

The order of frames in an environment affects the value returned by looking up a name in an expression. We stated previously that a name is evaluated to the value associated with that name in the current environment. We can now be more precise:

• A name evaluates to the value bound to that name in the earliest frame of the current environment in which that name is found.

Our conceptual framework of environments, names, and functions constitutes a model of evaluation; while some mechanical details are still unspecified (e.g., how a binding is implemented), our model does precisely and correctly describe how the interpreter evaluates call expressions. In Chapter 3 we will see how this model can serve as a blueprint for implementing a working interpreter for a programming language.

1.3.3   Example: Calling a User-Defined Function

Let us again consider our two simple function definitions and illustrate the process that evaluates a call expression for a user-defined function.

Python first evaluates the name sum_squares, which is bound to a user-defined function in the global frame. The primitive numeric expressions 5 and 12 evaluate to the numbers they represent.

Next, Python applies sum_squares, which introduces a local frame that binds x to 5 and y to 12.

The body of sum_squares contains this call expression:

  add     (  square(x)  ,  square(y)  )
________     _________     _________
operator     operand 0     operand 1

All three subexpressions are evalauted in the current environment, which begins with the frame labeled sum_squares(). The operator subexpression add is a name found in the global frame, bound to the built-in function for addition. The two operand subexpressions must be evaluated in turn, before addition is applied. Both operands are evaluated in the current environment beginning with the frame labeled sum_squares.

In operand 0, square names a user-defined function in the global frame, while x names the number 5 in the local frame. Python applies square to 5 by introducing yet another local frame that binds x to 5.

Using this environment, the expression mul(x, x) evaluates to 25.

Our evaluation procedure now turns to operand 1, for which y names the number 12. Python evaluates the body of square again, this time introducing yet another local frame that binds x to 12. Hence, operand 1 evaluates to 144.

Finally, applying addition to the arguments 25 and 144 yields a final return value for sum_squares: 169.

This example illustrates many of the fundamental ideas we have developed so far. Names are bound to values, which are distributed across many independent local frames, along with a single global frame that contains shared names. A new local frame is introduced every time a function is called, even if the same function is called twice.

All of this machinery exists to ensure that names resolve to the correct values at the correct times during program execution. This example illustrates why our model requires the complexity that we have introduced. All three local frames contain a binding for the name x, but that name is bound to different values in different frames. Local frames keep these names separate.

1.3.4   Local Names

One detail of a function's implementation that should not affect the function's behavior is the implementer's choice of names for the function's formal parameters. Thus, the following functions should provide the same behavior:

>>> def square(x):
        return mul(x, x)
>>> def square(y):
        return mul(y, y)

This principle -- that the meaning of a function should be independent of the parameter names chosen by its author -- has important consequences for programming languages. The simplest consequence is that the parameter names of a function must remain local to the body of the function.

If the parameters were not local to the bodies of their respective functions, then the parameter x in square could be confused with the parameter x in sum_squares. Critically, this is not the case: the binding for x in different local frames are unrelated. The model of computation is carefully designed to ensure this independence.

We say that the scope of a local name is limited to the body of the user-defined function that defines it. When a name is no longer accessible, it is out of scope. This scoping behavior isn't a new fact about our model; it is a consequence of the way environments work.

1.3.5   Practical Guidance: Choosing Names

The interchangeabily of names does not imply that formal parameter names do not matter at all. On the contrary, well-chosen function and parameter names are essential for the human interpretability of function definitions!

The following guidelines are adapted from the style guide for Python code, which serves as a guide for all (non-rebellious) Python programmers. A shared set of conventions smooths communication among members of a developer community. As a side effect of following these conventions, you will find that your code becomes more internally consistent.

1. Function names are lowercase, with words separated by underscores. Descriptive names are encouraged.
2. Function names typically evoke operations applied to arguments by the interpreter (e.g., print, add, square) or the name of the quantity that results (e.g., max, abs, sum).
3. Parameter names are lowercase, with words separated by underscores. Single-word names are preferred.
4. Parameter names should evoke the role of the parameter in the function, not just the kind of argument that is allowed.
5. Single letter parameter names are acceptable when their role is obvious, but avoid "l" (lowercase ell), "O" (capital oh), or "I" (capital i) to avoid confusion with numerals.

There are many exceptions to these guidelines, even in the Python standard library. Like the vocabulary of the English language, Python has inherited words from a variety of contributors, and the result is not always consistent.

1.3.6   Functions as Abstractions

Though it is very simple, sum_squares exemplifies the most powerful property of user-defined functions. The function sum_squares is defined in terms of the function square, but relies only on the relationship that square defines between its input arguments and its output values.

We can write sum_squares without concerning ourselves with how to square a number. The details of how the square is computed can be suppressed, to be considered at a later time. Indeed, as far as sum_squares is concerned, square is not a particular function body, but rather an abstraction of a function, a so-called functional abstraction. At this level of abstraction, any function that computes the square is equally good.

Thus, considering only the values they return, the following two functions for squaring a number should be indistinguishable. Each takes a numerical argument and produces the square of that number as the value.

>>> def square(x):
        return mul(x, x)
>>> def square(x):
        return mul(x, x-1) + x

In other words, a function definition should be able to suppress details. The users of the function may not have written the function themselves, but may have obtained it from another programmer as a "black box". A programmer should not need to know how the function is implemented in order to use it. The Python Library has this property. Many developers use the functions defined there, but few ever inspect their implementation.

To master the use of a functional abstraction, it is often useful to consider its three core attributes. The domain of a function is the set of arguments it can take. The range of a function is the set of values it can return. The intent of a function is the relationship it computes between inputs and output (as well as any side effects it might generate). Understanding functions via their domain, range, and intent is critical to using them correctly in a complex program.

1.3.7   Operators

Mathematical operators (like + and -) provided our first example of a method of combination, but we have yet to define an evaluation procedure for expressions that contain these operators.

Python expressions with infix operators each have their own evaluation procedures, but you can often think of them as short-hand for call expressions. When you see

>>> 2 + 3
5

simply consider it to be short-hand for

>>> add(2, 3)
5

Infix notation can be nested, just like call expressions. Python applies the normal mathematical rules of operator precedence, which dictate how to interpret a compound expression with multiple operators.

>>> 2 + 3 * 4 + 5
19

evaluates to the same result as

>>> add(add(2, mul(3, 4)), 5)
19

The nesting in the call expression is more explicit than the operator version, but also harder to read. Python also allows subexpression grouping with parentheses, to override the normal precedence rules or make the nested structure of an expression more explicit.

>>> (2 + 3) * (4 + 5)
45

evaluates to the same result as

>>> mul(add(2, 3), add(4, 5))
45

When it comes to division, Python provides two infix operators: / and //. The former is normal division, so that it results in a floating point, or decimal value, even if the divisor evenly divides the dividend:

>>> 5 / 4
1.25
>>> 8 / 4
2.0

The // operator, on the other hand, rounds the result down to an integer:

>>> 5 // 4
1
>>> -5 // 4
-2

These two operators are shorthand for the truediv and floordiv functions.

>>> from operator import truediv, floordiv
>>> truediv(5, 4)
1.25
>>> floordiv(5, 4)
1

You should feel free to use infix operators and parentheses in your programs. Idiomatic Python prefers operators over call expressions for simple mathematical operations.

1.4.1   Documentation

A function definition will often include documentation describing the function, called a docstring, which must be indented along with the function body. Docstrings are conventionally triple quoted. The first line describes the job of the function in one line. The following lines can describe arguments and clarify the behavior of the function:

>>> def pressure(v, t, n):
        """Compute the pressure in pascals of an ideal gas.

        Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas
        """
        k = 1.38e-23  # Boltzmann's constant
        return n * k * t / v

When you call help with the name of a function as an argument, you see its docstring (type q to quit Python help).

>>> help(pressure)

When writing Python programs, include docstrings for all but the simplest functions. Remember, code is written only once, but often read many times. The Python docs include docstring guidelines that maintain consistency across different Python projects.

Comments. Comments in Python can be attached to the end of a line following the # symbol. For example, the comment Boltzmann's constant above describes k. These comments don't ever appear in Python's help, and they are ignored by the interpreter. They exist for humans alone.

1.4.2   Default Argument Values

A consequence of defining general functions is the introduction of additional arguments. Functions with many arguments can be awkward to call and difficult to read.

In Python, we can provide default values for the arguments of a function. When calling that function, arguments with default values are optional. If they are not provided, then the default value is bound to the formal parameter name instead. For instance, if an application commonly computes pressure for one mole of particles, this value can be provided as a default:

>>> Boltzmann_K = 1.38e-23  # Boltzmann's constant
>>> def pressure(v, t, n=6.022e23):
        """Compute the pressure in pascals of an ideal gas.

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas (default: one mole)
        """
        return n * Boltzmann_K * t / v

The = symbol means two different things in this example, depending on the context in which it is used. In the first line above, = is the assignment operator. In the def statement header, = does not perform assignment, but instead indicates a default value to use when the pressure function is called.

>>> pressure(1, 273.15)
2269.974834
>>> pressure(1, 273.15, 3 * 6.022e23)
6809.924502

The pressure function is defined to take three arguments, but only two are provided in the first call expression above. In this case, the value for n is taken from the def statement default. If a third argument is provided, the default is ignored.

As a guideline, most data values used in a function's body should be expressed as default values to named arguments, so that they are easy to inspect and can be changed by the function caller. Some values that never change, such as the fundamental constant Boltzmann_K, can be bound in the global frame.

1.5.1   Statements

So far, we have primarily considered how to evaluate expressions. However, we have seen three kinds of statements already: assignment, def, and return statements. These lines of Python code are not themselves expressions, although they all contain expressions as components.

Rather than being evaluated, statements are executed. Each statement describes some change to the interpreter state, and executing a statement applies that change. As we have seen for return and assignment statements, executing statements can involve evaluating subexpressions contained within them.

Expressions can also be executed as statements, in which case they are evaluated, but their value is discarded. Executing a pure function has no effect, but executing a non-pure function can cause effects as a consequence of function application.

Consider, for instance,

>>> def square(x):
        mul(x, x) # Watch out! This call doesn't return a value.

This example is valid Python, but probably not what was intended. The body of the function consists of an expression. An expression by itself is a valid statement, but the effect of the statement is that the mul function is called, and the result is discarded. If you want to do something with the result of an expression, you need to say so: you might store it with an assignment statement or return it with a return statement:

>>> def square(x):
        return mul(x, x)

Sometimes it does make sense to have a function whose body is an expression, when a non-pure function like print is called.

>>> def print_square(x):
        print(square(x))

At its highest level, the Python interpreter's job is to execute programs, composed of statements. However, much of the interesting work of computation comes from evaluating expressions. Statements govern the relationship among different expressions in a program and what happens to their results.

1.5.2   Compound Statements

In general, Python code is a sequence of statements. A simple statement is a single line that doesn't end in a colon. A compound statement is so called because it is composed of other statements (simple and compound). Compound statements typically span multiple lines and start with a one-line header ending in a colon, which identifies the type of statement. Together, a header and an indented suite of statements is called a clause. A compound statement consists of one or more clauses:

<header>:
    <statement>
    <statement>
    ...
<separating header>:
    <statement>
    <statement>
    ...
...

We can understand the statements we have already introduced in these terms.

• Expressions, return statements, and assignment statements are simple statements.
• A def statement is a compound statement. The suite that follows the def header defines the function body.

Specialized evaluation rules for each kind of header dictate when and if the statements in its suite are executed. We say that the header controls its suite. For example, in the case of def statements, we saw that the return expression is not evaluated immediately, but instead stored for later use when the defined function is eventually called.

We can also understand multi-line programs now.

• To execute a sequence of statements, execute the first statement. If that statement does not redirect control, then proceed to execute the rest of the sequence of statements, if any remain.

This definition exposes the essential structure of a recursively defined sequence: a sequence can be decomposed into its first element and the rest of its elements. The "rest" of a sequence of statements is itself a sequence of statements! Thus, we can recursively apply this execution rule. This view of sequences as recursive data structures will appear again in later chapters.

The important consequence of this rule is that statements are executed in order, but later statements may never be reached, because of redirected control.

Practical Guidance. When indenting a suite, all lines must be indented the same amount and in the same way (use spaces, not tabs). Any variation in indentation will cause an error.

1.5.3   Defining Functions II: Local Assignment

Originally, we stated that the body of a user-defined function consisted only of a return statement with a single return expression. In fact, functions can define a sequence of operations that extends beyond a single expression.

Whenever a user-defined function is applied, the sequence of clauses in the suite of its definition is executed in a local environment. A return statement redirects control: the process of function application terminates whenever the first return statement is executed, and the value of the return expression is the returned value of the function being applied.

Thus, assignment statements can now appear within a function body. For instance, this function returns the absolute difference between two quantities as a percentage of the first, using a two-step calculation:

The effect of an assignment statement is to bind a name to a value in the first frame of the current environment. As a consequence, assignment statements within a function body cannot affect the global frame. The fact that functions can only manipulate their local environment is critical to creating modular programs, in which pure functions interact only via the values they take and return.

Of course, the percent_difference function could be written as a single expression, as shown below, but the return expression is more complex.

>>> def percent_difference(x, y):
        return 100 * abs(x-y) / x
>>> percent_difference(40, 50)
25.0

So far, local assignment hasn't increased the expressive power of our function definitions. It will do so, when combined with other control statements. In addition, local assignment also plays a critical role in clarifying the meaning of complex expressions by assigning names to intermediate quantities.

1.5.4   Conditional Statements

Python has a built-in function for computing absolute values.

>>> abs(-2)
2

We would like to be able to implement such a function ourselves, but we have no obvious way to define a function that has a comparison and a choice. We would like to express that if x is positive, abs(x) returns x. Furthermore, if x is 0, abs(x) returns 0. Otherwise, abs(x) returns -x. In Python, we can express this choice with a conditional statement.

This implementation of absolute_value raises several important issues:

Conditional statements. A conditional statement in Python consists of a series of headers and suites: a required if clause, an optional sequence of elif clauses, and finally an optional else clause:

if <expression>:
    <suite>
elif <expression>:
    <suite>
else:
    <suite>

When executing a conditional statement, each clause is considered in order. The computational process of executing a conditional clause follows.

1. Evaluate the header's expression.
2. If it is a true value, execute the suite. Then, skip over all subsequent clauses in the conditional statement.

If the else clause is reached (which only happens if all if and elif expressions evaluate to false values), its suite is executed.

Boolean contexts. Above, the execution procedures mention "a false value" and "a true value." The expressions inside the header statements of conditional blocks are said to be in boolean contexts: their truth values matter to control flow, but otherwise their values are not assigned or returned. Python includes several false values, including 0, None, and the boolean value False. All other numbers are true values. In Chapter 2, we will see that every built-in kind of data in Python has both true and false values.

Boolean values. Python has two boolean values, called True and False. Boolean values represent truth values in logical expressions. The built-in comparison operations, >, <, >=, <=, ==, !=, return these values.

>>> 4 < 2
False
>>> 5 >= 5
True

This second example reads "5 is greater than or equal to 5", and corresponds to the function ge in the operator module.

>>> 0 == -0
True

This final example reads "0 equals -0", and corresponds to eq in the operator module. Notice that Python distinguishes assignment (=) from equality comparison (==), a convention shared across many programming languages.

Boolean operators. Three basic logical operators are also built into Python:

>>> True and False
False
>>> True or False
True
>>> not False
True

Logical expressions have corresponding evaluation procedures. These procedures exploit the fact that the truth value of a logical expression can sometimes be determined without evaluating all of its subexpressions, a feature called short-circuiting.

To evaluate the expression <left> and <right>:

1. Evaluate the subexpression <left>.
2. If the result is a false value v, then the expression evaluates to v.
3. Otherwise, the expression evaluates to the value of the subexpression <right>.

To evaluate the expression <left> or <right>:

1. Evaluate the subexpression <left>.
2. If the result is a true value v, then the expression evaluates to v.
3. Otherwise, the expression evaluates to the value of the subexpression <right>.

To evaluate the expression not <exp>:

1. Evaluate <exp>; The value is True if the result is a false value, and False otherwise.

These values, rules, and operators provide us with a way to combine the results of comparisons. Functions that perform comparisons and return boolean values typically begin with is, not followed by an underscore (e.g., isfinite, isdigit, isinstance, etc.).

1.5.5   Iteration

In addition to selecting which statements to execute, control statements are used to express repetition. If each line of code we wrote were only executed once, programming would be a very unproductive exercise. Only through repeated execution of statements do we unlock the full potential of computers. We have already seen one form of repetition: a function can be applied many times, although it is only defined once. Iterative control structures are another mechanism for executing the same statements many times.

Consider the sequence of Fibonacci numbers, in which each number is the sum of the preceding two:

0, 1, 1, 2, 3, 5, 8, 13, 21, ...

Each value is constructed by repeatedly applying the sum-previous-two rule. The first and second are fixed to 0 and 1. For instance, the eighth Fibonacci number is 13.

We can use a while statement to enumerate n Fibonacci numbers. We need to track how many values we've created (k), along with the kth value (curr) and its predecessor (pred). Step through this function and observe how the Fibonacci numbers evolve one by one, bound to curr.

Remember that commas seperate multiple names and values in an assignment statement. The line:

pred, curr = curr, pred + curr

has the effect of rebinding the name pred to the value of curr, and simultanously rebinding curr to the value of pred + curr. All of the expressions to the right of = are evaluated before any rebinding takes place.

This order of events -- evaluating everything on the right of = before updating any bindings on the left -- is essential for correctness of this function.

A while clause contains a header expression followed by a suite:

while <expression>:
    <suite>

To execute a while clause:

1. Evaluate the header's expression.
2. If it is a true value, execute the suite, then return to step 1.

In step 2, the entire suite of the while clause is executed before the header expression is evaluated again.

In order to prevent the suite of a while clause from being executed indefinitely, the suite should always change some binding in each pass.

A while statement that does not terminate is called an infinite loop. Press <Control>-C to force Python to stop looping.

1.5.6   Practical Guidance: Testing

Testing a function is the act of verifying that the function's behavior matches expectations. Our language of functions is now sufficiently complex that we need to start testing our implementations.

A test is a mechanism for systematically performing this verification. Tests typically take the form of another function that contains one or more sample calls to the function being tested. The returned value is then verified against an expected result. Unlike most functions, which are meant to be general, tests involve selecting and validating calls with specific argument values. Tests also serve as documentation: they demonstrate how to call a function and what argument values are appropriate.

Assertions. Programmers use assert statements to verify expectations, such as the output of a function being tested. An assert statement has an expression in a boolean context, followed by a quoted line of text (single or double quotes are both fine, but be consistent) that will be displayed if the expression evaluates to a false value.

>>> assert fib(8) == 13, 'The 8th Fibonacci number should be 13'

When the expression being asserted evaluates to a true value, executing an assert statement has no effect. When it is a false value, assert causes an error that halts execution.

A test function for fib should test several arguments, including extreme values of n.

>>> def fib_test():
        assert fib(2) == 1, 'The 2nd Fibonacci number should be 1'
        assert fib(3) == 1, 'The 3rd Fibonacci number should be 1'
        assert fib(50) == 7778742049, 'Error at the 50th Fibonacci number'

When writing Python in files, rather than directly into the interpreter, tests are typically written in the same file or a neighboring file with the suffix _test.py.

Doctests. Python provides a convenient method for placing simple tests directly in the docstring of a function. The first line of a docstring should contain a one-line description of the function, followed by a blank line. A detailed description of arguments and behavior may follow. In addition, the docstring may include a sample interactive session that calls the function:

>>> def sum_naturals(n):
        """Return the sum of the first n natural numbers.

        >>> sum_naturals(10)
        55
        >>> sum_naturals(100)
        5050
        """
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total

Then, the interaction can be verified via the doctest module. Below, the globals function returns a representation of the global environment, which the interpreter needs in order to evaluate expressions.

>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)

To verify the doctest interactions for only a single function, we use a doctest function called run_docstring_examples. This function is (unfortunately) a bit complicated to call. Its first argument is the function to test. The second should always be the result of the expression globals(), a built-in function that returns the global environment. The third argument is True to indicate that we would like "verbose" output: a catalog of all tests run.

>>> from doctest import run_docstring_examples
>>> run_docstring_examples(sum_naturals, globals(), True)
Finding tests in NoName
Trying:
    sum_naturals(10)
Expecting:
    55
ok
Trying:
    sum_naturals(100)
Expecting:
    5050
ok

When the return value of a function does not match the expected result, the run_docstring_examples function will report this problem as a test failure.

When writing Python in files, all doctests in a file can be run by starting Python with the doctest command line option:

python3 -m doctest <python_source_file>

The key to effective testing is to write (and run) tests immediately after implementing new functions. It is even good practice to write some tests before you implement, in order to have some example inputs and outputs in your mind. A test that applies a single function is called a unit test. Exhaustive unit testing is a hallmark of good program design.

1.6.1   Functions as Arguments

Consider the following three functions, which all compute summations. The first, sum_naturals, computes the sum of natural numbers up to n:

>>> def sum_naturals(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total

>>> sum_naturals(100)
5050

The second, sum_cubes, computes the sum of the cubes of natural numbers up to n.

>>> def sum_cubes(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + pow(k, 3), k + 1
        return total

>>> sum_cubes(100)
25502500

The third, pi_sum, computes the sum of terms in the series

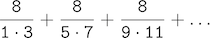
which converges to pi very slowly.

>>> def pi_sum(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + 8 / (k * (k + 2)), k + 4
        return total

>>> pi_sum(100)
3.121594652591009

These three functions clearly share a common underlying pattern. They are for the most part identical, differing only in name, the function of k used to compute the term to be added, and the function that provides the next value of k. We could generate each of the functions by filling in slots in the same template:

def <name>(n):
    total, k = 0, 1
    while k <= n:
        total, k = total + <term>(k), <next>(k)
    return total

The presence of such a common pattern is strong evidence that there is a useful abstraction waiting to be brought to the surface. Each of these functions is a summation of terms. As program designers, we would like our language to be powerful enough so that we can write a function that expresses the concept of summation itself rather than only functions that compute particular sums. We can do so readily in Python by taking the common template shown above and transforming the "slots" into formal parameters:

In the example below, summation takes as its three arguments the upper bound n together with the functions term and next. We can use summation just as we would any function, and it expresses summations succinctly. Take the time to step through this example, and notice how binding cube and successor to the local names term and next ensures that the result 1*1*1 + 2*2*2 + 3*3*3 = 36 is computed correctly. In this example, frames which are no longer needed are removed to save space.

Using an identity function that returns its argument, we can also sum natural numbers.

>>> def identity(k):
        return k

>>> def sum_naturals(n):
        return summation(n, identity, successor)

>>> sum_naturals(10)
55

We can define pi_sum in terms of term and next functions, using our summation abstraction to combine components. We pass the argument 1e6, a shorthand for 1 * 10^6 = 1000000, to generate a close approximation to pi.

>>> def pi_term(k):
        denominator = k * (k + 2)
        return 8 / denominator

>>> def pi_next(k):
        return k + 4

>>> def pi_sum(n):
        return summation(n, pi_term, pi_next)

>>> pi_sum(1e6)
3.1415906535898936

1.6.2   Functions as General Methods

We introduced user-defined functions as a mechanism for abstracting patterns of numerical operations so as to make them independent of the particular numbers involved. With higher-order functions, we begin to see a more powerful kind of abstraction: some functions express general methods of computation, independent of the particular functions they call.

Despite this conceptual extension of what a function means, our environment model of how to evaluate a call expression extends gracefully to the case of higher-order functions, without change. When a user-defined function is applied to some arguments, the formal parameters are bound to the values of those arguments (which may be functions) in a new local frame.

Consider the following example, which implements a general method for iterative improvement and uses it to compute the golden ratio. An iterative improvement algorithm begins with a guess of a solution to an equation. It repeatedly applies an update function to improve that guess, and applies an isclose comparison to check whether the current guess is "close enough" to be considered correct.

>>> def improve(update, isclose, guess=1):
        while not isclose(guess):
            guess = update(guess)
        return guess

One way to know if the current guess "isclose" is to check whether two functions, f and g, are near to each other for that guess. Testing whether f(x) is near to g(x) is again a general method of computation.

>>> def near(x, f, g):
        return approx_eq(f(x), g(x))

A common way to test for approximate equality in programs is to compare the absolute value of the difference between numbers to a small tolerance value.

>>> def approx_eq(x, y, tolerance=1e-3):
        return abs(x - y) < tolerance

The golden ratio, often called "phi", is a number that appears frequently in nature, art, and architecture. It can be computed via improve using the golden_update, and it converges when its successor is equal to its square.

>>> def golden_update(guess):
        return 1/guess + 1

>>> def square_near_successor(guess):
        return near(guess, square, successor)

Calling improve with the arguments golden_update and square_near_successor will compute an approximation to the golden ratio.

>>> improve(golden_update, square_near_successor)
1.6180371352785146

By tracing through the steps of evaluation, we can see how this result is computed. First, a local frame for improve is constructed with bindings for update, isclose, and guess. In the body of improve, the name isclose is bound to square_near_successor, which is called on the initial value of guess. In turn, square_near_successor calls near, creating a third local frame that binds the formal parameters f and g to square and successor.

Completing the evaluation of near, we see that the square_near_successor is False because 1 is not close to 2. Hence, evaluation proceeds with the suite of the while clause, and this mechanical process repeats several times.

This extended example illustrates two related big ideas in computer science. First, naming and functions allow us to abstract away a vast amount of complexity. While each function definition has been trivial, the computational process set in motion by our evaluation procedure appears quite intricate. Second, it is only by virtue of the fact that we have an extremely general evaluation procedure that small components can be composed into complex processes. Understanding that procedure allows us to validate and inspect the process we have created.

As always, our new general method improve needs a test to check its correctness. The golden ratio can provide such a test, because it also has an exact closed-form solution, which we can compare to this iterative result.

>>> phi = 1/2 + pow(5, 1/2)/2
>>> def near_test():
        assert near(phi, square, successor), 'phi * phi is not near phi + 1'

>>> def improve_test():
        approx_phi = improve(golden_update, square_near_successor)
        assert approx_eq(phi, approx_phi), 'phi differs from its approximation'

Extra for experts. We left out a step in the justification of our test. For what range of tolerance values e can you prove that if near(x, square, successor) is true with tolerance value e, then approx_eq(phi, x) is true with the same tolerance?

1.6.3   Defining Functions III: Nested Definitions

The above examples demonstrate how the ability to pass functions as arguments significantly enhances the expressive power of our programming language. Each general concept or equation maps onto its own short function. One negative consequence of this approach is that the global frame becomes cluttered with names of small functions, which must all be unique. Another problem is that we are constrained by particular function signatures: the update argument to improve must take exactly one argument. Nested function definitions address both of these problems, but require us to enrich our environment model.

Let's consider a new problem: computing the square root of a number. In programming languages, "square root" is often abbreviated as sqrt. Repeated application of the following update converges to the square root of x:

>>> def average(x, y):
        return (x + y)/2

>>> def sqrt_update(guess, x):
        return average(guess, x/guess)

This two-argument update function is incompatible with improve (it takes two arguments, not one), and it provides only a single update, while we really care about taking square roots by repeated updates. The solution to both of these issues is to place function definitions inside the body of other definitions.

>>> def sqrt(x):
        def sqrt_update(guess):
            return average(guess, x/guess)
        def sqrt_close(guess):
            return approx_eq(square(guess), x)
        return improve(sqrt_update, sqrt_close)

Like local assignment, local def statements only affect the current local frame. These functions are only in scope while sqrt is being evaluated. Consistent with our evaluation procedure, these local def statements don't even get evaluated until sqrt is called.

Lexical scope. Locally defined functions also have access to the name bindings in the scope in which they are defined. In this example, sqrt_update refers to the name x, which is a formal parameter of its enclosing function sqrt. This discipline of sharing names among nested definitions is called lexical scoping. Critically, the inner functions have access to the names in the environment where they are defined (not where they are called).

We require two extensions to our environment model to enable lexical scoping.

1. Each user-defined function has a parent environment: the environment in which it was defined.
2. When a user-defined function is called, its local frame extends its parent environment.

Previous to sqrt, all functions were defined in the global environment, and so they all had the same parent: the global environment. By contrast, when Python evaluates the first two clauses of sqrt, it create functions that are associated with a local environment. In the call

>>> sqrt(256)
16.000000002151005

the environment first adds a local frame for sqrt and evaluates the def statements for sqrt_update and sqrt_close.

The function values for sqrt_update and sqrt_close each has a new annotation: a parent. The parent of a function value is the first frame of the environment in which that function was defined. Functions without parent annotations were defined in the global environment. In order to annotate the parent of sqrt_update, we give the frame sqrt a label, f1, and refer to that label. We only label frames that we need to reference.

Subsequently, the name sqrt_update resolves to this newly defined function, which is passed as an argument to improve. Within the body of improve, we must apply our update function (bound to sqrt_update) to the initial guess of 1. This final application creates an environment for sqrt_update that begins with a local frame containing only guess, but with the parent frame sqrt still containing a binding for x.

The most critical part of this evaluation procedure is the transfer of the parent for sqrt_update to the frame created by calling sqrt_update. This frame is also annotated with [parent=f1].

Extended Environments. An environment can consist of an arbitrarily long chain of frames, which always concludes with the global frame. Previous to this sqrt example, environments had at most two frames: a local frame and the global frame. By calling functions that were defined within other functions, via nested def statements, we can create longer chains. The environment for this call to sqrt_update consists of three frames: the local sqrt_update frame, the sqrt frame in which sqrt_update was defined (labeled f1), and the global frame.

The return expression in the body of sqrt_update can resolve a value for x by following this chain of frames. Recall that looking up a name finds the first value bound to that name in the current environment. Python checks first in the sqrt_update frame -- no x exists. Python checks next in the parent frame, f1, and finds a binding for x to 256.

Hence, we realize two key advantages of lexical scoping in Python.

• The names of a local function do not interfere with names external to the function in which it is defined, because the local function name will be bound in the current local environment in which it was defined, rather than the global environment.
• A local function can access the environment of the enclosing function, because the body of the local function is evaluated in an environment that extends the evaluation environment in which it was defined.

The sqrt_update function carries with it some data: the value for x referenced in the environment in which it was defined. Because they "enclose" information in this way, locally defined functions are often called closures.

1.6.4   Functions as Returned Values

We can achieve even more expressive power in our programs by creating functions whose returned values are themselves functions. An important feature of lexically scoped programming languages is that locally defined functions maintain their parent environment when they are returned. The following example illustrates the utility of this feature.

Once many simple functions are defined, function composition is a natural method of combination to include in our programming language. That is, given two functions f(x) and g(x), we might want to define h(x) = f(g(x)). We can define function composition using our existing tools:

>>> def compose1(f, g):
        def h(x):
            return f(g(x))
        return h

The environment diagram for this example shows how the names f and g are resolved correctly, even in the presence of conflicting names.

The 1 in compose1 is meant to signify that the composed functions all take a single argument. This naming convention is not enforced by the interpreter; the 1 is just part of the function name.

At this point, we begin to observe the benefits of our effort to define precisely the environment model of computation. No modification to our environment model is required to explain our ability to return functions in this way.

1.6.5   Currying

We can use higher-order functions to convert a function that takes multiple arguments into a chain of functions that each take a single argument. More specifically, given a function f(x, y), we can define a function g such that g(x)(y) is equivalent to f(x, y). Here, g is a higher-order function that takes in a single argument x and returns another function that takes in a single argument y. This transformation is called currying.

As an example, we can define a curried version of the pow function:

>>> def curried_pow(x):
        def h(y):
            return pow(x, y)
        return h

>>> curried_pow(2)(3)
8

Some programming languages, such as Haskell, only allow functions that take a single argument, so the programmer must curry all multi-argument procedures. In more general languages such as Python, currying is useful when we require a function that takes in only a single argument. For example, the map pattern applies a single-argument function to a sequence of values. In later chapters, we will see more general examples of the map pattern, but for now, we can implement the pattern in a function:

>>> def map_to_range(start, end, f):
        while start < end:
            print(f(start))
            start = start + 1

We can use map_to_range and curried_pow to compute the first ten powers of two, rather than specifically writing a function to do so:

>>> map_to_range(0, 10, curried_pow(2))
1
2
4
8
16
32
64
128
256
512

We can similarly use the same two functions to compute powers of other numbers. Currying allows us to do so without writing a specific function for each number whose powers we wish to compute.

In the above examples, we manually performed the currying transformation on the pow function to obtain curried_pow. Instead, we can define functions to automate currying, as well as the inverse uncurrying transformation:

>>> def curry2(f):
        """Return a curried version of the given two-argument function."""
        def g(x):
            def h(y):
                return f(x, y)
            return h
        return g

>>> def uncurry2(g):
        """Return a two-argument version of the given curried function."""
        def f(x, y):
            return g(x)(y)
        return f

>>> a = curry2(pow)
>>> map_to_range(0, 10, a(2))
1
2
4
8
16
32
64
128
256
512

The curry2 function takes in a two-argument function f and returns a single-argument function g. When g is applied to an argument x, it returns a single-argument function h. When h is applied to y, it calls f(x, y). Thus, curry2(f)(x)(y) is equivalent to f(x, y), so curry2(f) returns a curried version of f.

The uncurry2 function should reverse the currying transformation, so that uncurry2(curry2(f)) is equivalent to f. We leave the argument that this is indeed the case as an exercise.

1.6.6   Lambda Expressions

So far, each time we have wanted to define a new function, we needed to give it a name. But for other types of expressions, we don't need to associate intermediate values with a name. That is, we can compute a*b + c*d without having to name the subexpressions a*b or c*d, or the full expression. In Python, we can create function values on the fly using lambda expressions, which evaluate to unnamed functions. A lambda expression evaluates to a function that has a single return expression as its body. Assignment and control statements are not allowed.

Lambda expressions are limited: They are only useful for simple, one-line functions that evaluate and return a single expression. In those special cases where they apply, lambda expressions can be quite expressive.

>>> def compose1(f, g):
        return lambda x: f(g(x))

We can understand the structure of a lambda expression by constructing a corresponding English sentence:

     lambda            x            :          f(g(x))
"A function that    takes x    and returns     f(g(x))"

The result of a lambda expression is called a lambda function. It has no intrinsic name (and so Python prints <lambda> for the name), but otherwise behaves like any other function.

>>> s = lambda x: x * x
>>> s
<function <lambda> at 0xf3f490>
>>> s(12)
144

In an environment diagram, the result of a lambda expression is a function as well, named with the greek letter λ (lambda). Our compose example can be expressed quite compactly with lambda expressions.

Some programmers find that using unnamed functions from lambda expressions to be shorter and more direct. However, compound lambda expressions are notoriously illegible, despite their brevity. The following definition is correct, but many programmers have trouble understanding it quickly.

>>> compose1 = lambda f,g: lambda x: f(g(x))

In general, Python style prefers explicit def statements to lambda expressions, but allows them in cases where a simple function is needed as an argument or return value.

Such stylistic rules are merely guidelines; you can program any way you wish. However, as you write programs, think about the audience of people who might read your program one day. When you can make your program easier to understand, you do those people a favor.

The term lambda is a historical accident resulting from the incompatibility of written mathematical notation and the constraints of early type-setting systems.

It may seem perverse to use lambda to introduce a procedure/function. The notation goes back to Alonzo Church, who in the 1930's started with a "hat" symbol; he wrote the square function as "ŷ . y × y". But frustrated typographers moved the hat to the left of the parameter and changed it to a capital lambda: "Λy . y × y"; from there the capital lambda was changed to lowercase, and now we see "λy . y × y" in math books and (lambda (y) (* y y)) in Lisp.

—Peter Norvig (norvig.com/lispy2.html)

Despite their unusual etymology, lambda expressions and the corresponding formal language for function application, the lambda calculus, are fundamental computer science concepts shared far beyond the Python programming community. We will revisit this topic when we study the design of interpreters in Chapter 3.

1.6.7   Example: Newton's Method

This final extended example shows how function values, local defintions, and lambda expressions can work together to express general ideas concisely.

Newton's method is a classic iterative approach to finding the arguments of a mathematical function that yield a return value of 0. These values are called roots of a single-argument mathematical function. Finding a root of a function is often equivalent to solving a related math problem.

• The square root of 16 is the value x such that: square(x) - 16 = 0
• The log base 2 of 32 (i.e., the exponent to which we would raise 2 to get 32) is the value x such that: pow(2, x) - 32 = 0

Thus, a general method for finding roots will also provide us an algorithm to compute square roots and logarithms. Moreover, the equations for which we want to compute roots only contain simpler operations: multiplication and exponentiation.

A comment before we proceed: it is easy to take for granted the fact that we know how to compute square roots and logarithms. Not just Python, but your phone, your pocket calculator, and perhaps even your watch can do so for you. However, part of learning computer science is understanding how quantities like these can be computed, and the general approach presented here is applicable to solving a large class of equations beyond those built into Python.

Before even beginning to understand Newton's method, we can start programming; this is the power of functional abstractions. We simply translate our previous statements into code.

>>> def sqrt(a):
        return find_root(lambda x: square(x) - a)

>>> def logarithm(a, base=2):
        return find_root(lambda x: pow(base, x) - a)

Of course, we cannot apply any of these functions until we define find_root, and so we need to understand how Newton's method works.

Newton's method is also an iterative improvement algorithm: it improves a guess of the root for any function that is differentiable. Notice that both of our functions of interest change smoothly; graphing x versus f(x) for

• f(x) = square(x) - 16 (light curve)
• g(x) = pow(2, x) - 32 (dark curve)

on a 2-dimensional plane shows that each function defines a smooth curve without kinks that crosses 0 at the appropriate point (4 for f, 5 for g).

Because they are smooth (differentiable), these curves can be approximated by a line at any point. Newton's method follows these linear approximations to find function roots.

Imagine a line through the point (x, f(x)) that has the same slope as the curve for function f(x) at that point. Such a line is called the tangent, and its slope is called the derivative of f at x.

This line's slope is the ratio of the change in function value to the change in function argument. Hence, translating x by f(x) divided by the slope will give the argument value at which this tangent line touches 0.

Our Newton update expresses the computational process of following this tangent line to 0. We approximate the derivative of the function by computing its slope over a very small interval.

>>> def approx_derivative(f, x, delta=1e-5):
        df = f(x + delta) - f(x)
        return df/delta

>>> def newton_update(f):
        def update(x):
            return x - f(x) / approx_derivative(f, x)
        return update

Finally, we can define the find_root function in terms of newton_update, our iterative improvement algorithm, and a comparison to see if f(x) is near 0. We supply a larger initial guess to improve performance for logarithm.

>>> def find_root(f, initial_guess=10):
        def close_to_zero(x):
            return approx_eq(f(x), 0)
        return improve(newton_update(f), close_to_zero, initial_guess)

>>> sqrt(16)
4.000010374778599
>>> logarithm(32, 2)
5.000000094858201

As you experiment with Newton's method, be aware that it will not always converge. The initial guess of improve must be sufficiently close to the root, and various conditions about the function must be met. Despite this shortcoming, Newton's method is a powerful general computational method for solving differentiable equations. In fact, very fast algorithms for logarithms and large integer division employ variants of the technique in modern computers.

1.6.8   Abstractions and First-Class Functions

We began this section with the observation that user-defined functions are a crucial abstraction mechanism, because they permit us to express general methods of computing as explicit elements in our programming language. Now we've seen how higher-order functions permit us to manipulate these general methods to create further abstractions.

As programmers, we should be alert to opportunities to identify the underlying abstractions in our programs, build upon them, and generalize them to create more powerful abstractions. This is not to say that one should always write programs in the most abstract way possible; expert programmers know how to choose the level of abstraction appropriate to their task. But it is important to be able to think in terms of these abstractions, so that we can be ready to apply them in new contexts. The significance of higher-order functions is that they enable us to represent these abstractions explicitly as elements in our programming language, so that they can be handled just like other computational elements.

In general, programming languages impose restrictions on the ways in which computational elements can be manipulated. Elements with the fewest restrictions are said to have first-class status. Some of the "rights and privileges" of first-class elements are:

1. They may be bound to names.
2. They may be passed as arguments to functions.
3. They may be returned as the results of functions.
4. They may be included in data structures.

Python awards functions full first-class status, and the resulting gain in expressive power is enormous.

1.6.9   Function Decorators

Python provides special syntax to apply higher-order functions as part of executing a def statement, called a decorator. Perhaps the most common example is a trace.

>>> def trace1(fn):
        def wrapped(x):
            print('-> ', fn, '(', x, ')')
            return fn(x)
        return wrapped

>>> @trace1
    def triple(x):
        return 3 * x

>>> triple(12)
->  <function triple at 0x102a39848> ( 12 )
36

In this example, A higher-order function trace1 is defined, which returns a function that precedes a call to its argument with a print statement that outputs the argument. The def statement for triple has an annototation, @trace1, which affects the execution rule for def. As usual, the function triple is created. However, the name triple is not bound to this function. Instead, the name triple is bound to the returned function value of calling trace1 on the newly defined triple function. In code, this decorator is equivalent to:

>>> def triple(x):
        return 3 * x

>>> triple = trace1(triple)

In the projects associated with this text, decorators are used for tracing, as well as selecting which functions to call when a program is run from the command line.

Extra for experts. The decorator symbol @ may also be followed by a call expression. The expression following @ is evaluated first (just as the name trace was evaluated above), the def statement second, and finally the result of evaluating the decorator expression is applied to the newly defined function, and the result is bound to the name in the def statement. A short tutorial on decorators by Ariel Ortiz gives further examples for interested students.

1.7.1   Recursive Functions

A function is called recursive if the body of that function calls the function itself, either directly or indirectly. That is, the process of executing the body of a recursive function may in turn require applying that function again. Recursive functions do not use any special syntax in Python, but they do require some care to define correctly.

As an introduction to recursive functions, we begin with the task of converting an English word into its Pig Latin equivalent. Pig Latin is a secret language: one that applies a simple, deterministic transformation to each word that veils the meaning of the word. Thomas Jefferson was supposedly an early adopter. The Pig Latin equivalent of an English word moves the initial consonant cluster (which may be empty) from the beginning of the word to the end and follows it by the "-ay" vowel. Hence, the word "pun" becomes "unpay", "stout" becomes "outstay", and "all" becomes "allay".

Our goal in this section is to define a set of functions to produce the Pig Latin version of a word. We use strings to represent words, but we need a way of separately accessing the first letter of a word and the remaining letters. We can use the expression s[0] to obtain the first letter of a string s and s[1:] to get the remaining letters:

>>> 'pig'[0]
'p'
>>> 'pig'[1:]
'ig'

The bracket notation is very general and will be discussed at length in Chapter 2, but this is all we need for now. We can now define functions to produce the Pig Latin version of a word:

>>> def pig_latin(w):
        """Return the Pig Latin equivalent of a lowercase English word w."""
        if starts_with_a_vowel(w):
            return w + 'ay'
        return pig_latin(w[1:] + w[0])

>>> def starts_with_a_vowel(w):
        """Return whether w begins with a vowel."""
        c = w[0]
        return c == 'a' or c == 'e' or c == 'i' or c == 'o' or c == 'u'

The idea behind this definition is that the Pig Latin variant of a string that starts with a consonant is the same as the Pig Latin variant of another string: that which is created by moving the first letter to the end. Hence, the Pig Latin word for "sending" is the same as for "endings" (endingsay), and the Pig Latin word for "smother" is the same as the Pig Latin word for "mothers" (othersmay). Moreover, moving one consonant from the beginning of the word to the end results in a simpler problem with fewer initial consonants. In the case of "sending", moving the "s" to the end gives a word that starts with a vowel, and so our work is done.

This definition of pig_latin is both complete and correct, even though the pig_latin function is called within its own body.

>>> pig_latin('pun')
'unpay'

The idea of being able to define a function in terms of itself may be disturbing; it may seem unclear how such a "circular" definition could make sense at all, much less specify a well-defined process to be carried out by a computer. We can, however, understand precisely how this recursive function applies successfully using our environment model of computation. The environment diagram and expression tree that depict the evaluation of pig_latin('pun') appear below.

The steps of the Python evaluation procedures that produce this result are:

1. The def statement for pig_latin is executed, which

1. Creates a new pig_latin function with the stated body, and
2. Binds the name pig_latin to that function in the current (global) frame.

2. The def statement for starts_with_a_vowel is executed similarly.
3. The call expression pig_latin('pun') is evaluated by

1. Evaluating the operator and operand sub-expressions by

1. Looking up the name pig_latin that is bound to the pig_latin function.
2. Evaluating the operand string literal to the string 'pun'.

2. Applying the function pig_latin to the argument 'pun' by

1. Adding a local frame,
2. Binding the formal parameter w to the argument 'pun' in that frame, and
3. Executing the body of pig_latin in the environment that starts with that frame:

1. The initial conditional statement has no effect, because the header expression evaluates to False.
2. The final return expression pig_latin(w[1:] + w[0]) is evaluated by

1. Looking up the name pig_latin that is bound to the pig_latin function,
2. Evaluating the operand expression to the string 'unp',
3. Applying pig_latin to the argument 'unp', which returns the desired result from the suite of the conditional statement in the body of pig_latin.

As this example illustrates, a recursive function applies correctly, despite its circular character. The pig_latin function is applied twice, but with a different argument each time. Although the second call comes from the body of pig_latin itself, looking up that function by name succeeds because the name pig_latin is bound in the environment before its body is executed.

This example also illustrates how Python's recursive evaluation procedure can interact with a recursive function to evolve a complex computational process with many nested steps, even though the function definition may itself contain very few lines of code. Some examples are quite long indeed: the word scythe results in the longest terminating pig_latin process among words that appear in Shakespeare's works, ignoring punctuation.

1.7.2   The Anatomy of Recursive Functions

A common pattern can be found in the body of many recursive functions. The body begins with a base case, a conditional statement that defines the behavior of the function for the inputs that are simplest to process. In the case of pig_latin, the base case occurs for any argument that starts with a vowel. In this case, there is no work left to be done but return the argument with "ay" added to the end. Some recursive functions will have multiple base cases.

The base cases are then followed by one or more recursive calls. Recursive calls require a certain character: they must simplify the original problem. In the case of pig_latin, the more initial consonants in w, the more work there is left to do. In the recursive call, pig_latin(w[1:] + w[0]), we call pig_latin on a word that has one fewer initial consonant: a simpler problem. Each successive call to pig_latin will be simpler still until the base case is reached: a word with no initial consonants (assuming that the input contains a vowel somewhere).

Recursive functions express computation by simplifying problems incrementally. They often operate on problems in a different way than the iterative approaches that we have used in the past. Consider a function fact to compute n factorial, where for example fact(4) computes \(4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24\).

A natural implementation using a while statement accumulates the total by multiplying together each positive integer up to n.

>>> def fact_iter(n):
        total, k = 1, 1
        while k <= n:
            total, k = total * k, k + 1
        return total

>>> fact_iter(4)
24

On the other hand, a recursive implementation of factorial can express fact(n) in terms of fact(n-1), a simpler problem. The base case of the recursion is the simplest form of the problem: fact(1) is 1.

These two factorial functions differ conceptually. The iterative function constructs the result from the base case of 1 to the final total by successively multiplying in each term. The recursive function, on the other hand, constructs the result directly from the final term, n, and the result of the simpler problem, fact(n-1).

As the recursion "unwinds" through successive applications of the fact function to simpler and simpler problem instances, the result is eventually built starting from the base case. The recursion ends by passing the argument 1 to fact; the result of each call depends on the next until the base case is reached.

The correctness of this recursive function is easy to verify from the standard definition of the mathematical function for factorial:

While we can unwind the recursion using our model of computation, it is often clearer to think about recursive calls as functional abstractions. That is, we should not care about how fact(n-1) is implemented in the body of fact; we should simply trust that it computes the factorial of n-1. Treating a recursive call as a functional abstraction has been called a recursive leap of faith. We define a function in terms of itself, but simply trust that the simpler cases will work correctly when verifying the correctness of the function. In this example, we trust that fact(n-1) will correctly compute (n-1)!; we must only check that n! is computed correctly if this assumption holds. In this way, verifying the correctness of a recursive function is a form of proof by induction.

The functions fact_iter and fact also differ because the former must introduce two additional names, total and k, that are not required in the recursive implementation. In general, iterative functions must maintain some local state that changes throughout the course of computation. At any point in the iteration, that state characterizes the result of completed work and the amount of work remaining. For example, when k is 3 and total is 2, there are still two terms remaining to be processed, 3 and 4. On the other hand, fact is characterized by its single argument n. The state of the computation is entirely contained within the structure of the environment, which has return values that take the role of total, and binds n to different values in different frames rather than explicitly tracking k.

Recursive functions can rely more heavily on the interpreter itself, by storing the state of the computation as part of the environment, rather than explicitly using names in the local frame. For this reason, recursive functions are often easier to define, because we do not need to try to determine the local state that must be maintained across iterations. On the other hand, learning to recognize the computational processes evolved by recursive functions requires practice.

1.7.3   Mutual Recursion

When a recursive procedure is divided among two functions that call each other, the functions are said to be mutually recursive. As an example, consider the following definition of even and odd for non-negative integers:

• a number is even if it is one more than an odd number
• a number is odd if it is one more than an even number
• 0 is even

Using this definition, we can implement mutually recursive functions to determine whether a number is even or odd:

Mutually recursive functions can be turned into a single recursive function by breaking the abstraction boundary between the two functions. In this example, the body of is_odd can be incorporated into that of is_even, making sure to replace n with n-1 in the body of is_odd to reflect the argument passed into it:

>>> def is_even(n):
        if n == 0:
            return True
        else:
            if (n-1) == 0:
                return False
            else:
                return is_even((n-1)-1)

As such, mutual recursion is no more mysterious or powerful than simple recursion, and it provides a mechanism for maintaining abstraction within a complicated recursive procedure.

As another example of mutual recursion, consider a two-player game in which there are n initial pebbles on a table. The players take turns, removing either one or two pebbles from the table, and the player who removes the final pebble wins. Suppose that Alice and Bob play this game, each using a simple strategy:

• Alice always removes a single pebble
• Bob removes two pebbles if an even number of pebbles is on the table, and one otherwise

Given n initial pebbles and Alice starting, who wins the game?

A natural decomposition of this problem is to encapsulate each strategy in its own function. This allows us to modify one strategy without affecting the other, maintaining the abstraction barrier between the two. In order to incorporate the turn-by-turn nature of the game, these two functions should call each other at the end of each turn.

>>> def play_alice(n):
        if n == 0:
            print("Bob wins!")
        else:
            play_bob(n-1)

>>> def play_bob(n):
        if n == 0:
            print("Alice wins!")
        elif is_even(n):
            play_alice(n-2)
        else:
            play_alice(n-1)

Two observations can be made from the above functions. First, a recursive procedure need not return any value. In this case, a different string is printed to the screen depending on who wins. Second, multiple recursive calls may appear in the body of a function. Here, play_bob may call play_alice from two locations in the body. However, in this example, each call to play_bob calls play_alice at most once. In the next section, we consider what happens when a single function call makes multiple direct recursive calls.

1.7.4   Tree Recursion

Another common pattern of computation is called tree recursion. As an example, consider computing the sequence of Fibonacci numbers, in which each number is the sum of the preceding two.

This recursive definition is tremendously appealing relative to our previous attempts: it exactly mirrors the familiar definition of Fibonacci numbers. Consider the pattern of computation that results from evaluating fib(6), shown below. To compute fib(6), we compute fib(5) and fib(4). To compute fib(5), we compute fib(4) and fib(3). In general, the evolved process looks like a tree (the diagram below is not a full environment diagram, but instead a simplified depiction of the process). Each blue dot indicates a completed computation of a Fibonacci number in the traversal of this tree.

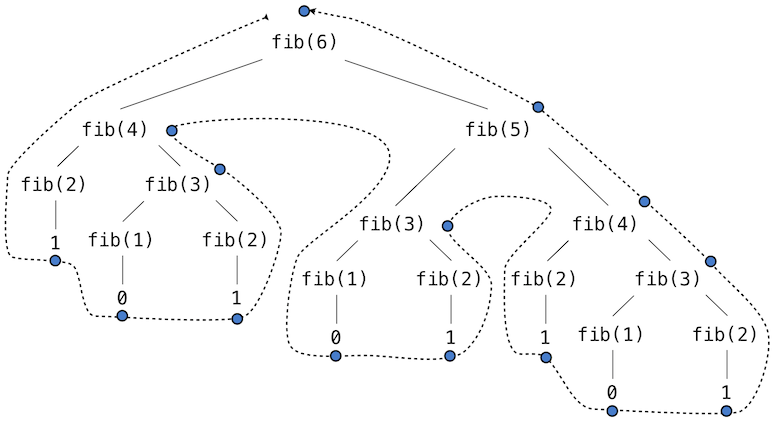
Functions that call themselves multiple times in this way are said to be tree recursive. This function is instructive as a prototypical tree recursion, but it is a terribly inefficient way to compute Fibonacci numbers because it does so much redundant computation. Notice that the entire computation of fib(4) -- almost half the work -- is duplicated. In fact, it is not hard to show that the number of times the function will compute fib(1) or fib(2) (the number of leaves in the tree, in general) is precisely fib(n+1). To get an idea of how bad this is, one can show that the value of fib(n) grows exponentially with n. fib(40) is 63,245,986! The function above uses a number of steps that grows exponentially with the input.

We have already seen an iterative implementation of Fibonacci numbers, repeated here for convenience.

>>> def fib_iter(n):
        prev, curr = 1, 0  # curr is the first Fibonacci number.
        for _ in range(n-1):
             prev, curr = curr, prev + curr
        return curr

The state that we must maintain in this case consists of the current and previous Fibonacci numbers. Implicitly, the for statement also keeps track of the iteration count. This definition does not reflect the standard mathematical definition of Fibonacci numbers as clearly as the recursive approach. However, the amount of computation required in the iterative implementation is only linear in n, rather than exponential. Even for small values of n, this difference can be enormous.

One should not conclude from this difference that tree-recursive processes are useless. When we consider processes that operate on hierarchically structured data rather than numbers, we will find that tree recursion is a natural and powerful tool. Furthermore, tree-recursive processes can often be made more efficient, as we will see in Chapter 3.

1.7.5   Example: Counting Change

Consider the following problem: How many different ways can we make change of $1.00, given half-dollars, quarters, dimes, nickels, and pennies? More generally, can we write a function to compute the number of ways to change any given amount of money using any set of currency denominations?

This problem has a simple solution as a recursive function. Suppose we think of the types of coins available as arranged in some order, say from most to least valuable.

The number of ways to change an amount a using n kinds of coins equals

1. the number of ways to change a using all but the first kind of coin, plus
2. the number of ways to change the smaller amount a - d using all n kinds of coins, where d is the denomination of the first kind of coin.

To see why this is true, observe that the ways to make change can be divided into two groups: those that do not use any of the first kind of coin, and those that do. Therefore, the total number of ways to make change for some amount is equal to the number of ways to make change for the amount without using any of the first kind of coin, plus the number of ways to make change assuming that we do use the first kind of coin at least once. But the latter number is equal to the number of ways to make change for the amount that remains after using a coin of the first kind.

Thus, we can recursively reduce the problem of changing a given amount to the problem of changing smaller amounts using fewer kinds of coins. Before we formulate an algorithm for this problem, we first need a means of encoding a decreasing sequence of coin denominations. We define the following function to do so:

>>> def next_coin(amount):
        """Return the largest coin that is smaller than amount, which must be a
        valid coin denomination in cents."""
        if amount == 1:
            return 0
        elif amount == 5:
            return 1
        elif amount == 25:
            return 10
        else:
            return amount // 2

Given a valid US coin value, the next_coin function determines the next largest valid US coin. (The // operator performs division and produces a rounded-down integer, unlike /, which produces a decimal or floating point number even if the division result is an integer.) Thus, we can iterate through all coins by repeatedly calling next_coin, starting from the largest value, until we reach 0:

>>> a = 50
>>> print(a)
50
>>> a = next_coin(a)
>>> print(a)
25
>>> a = next_coin(a)
>>> print(a)
10
>>> a = next_coin(a)
>>> print(a)
5
>>> a = next_coin(a)
>>> print(a)
1
>>> a = next_coin(a)
>>> print(a)
0

The next_coin function provides an abstraction of a sequence of coins. We can define similar functions for currencies other than USD.

Now we can define a function for counting the number of ways to make change. Consider this reduction rule carefully and convince yourself that we can use it to describe an algorithm if we specify the following base cases:

1. If a is exactly 0, we should count that as 1 way to make change.
2. If a is less than 0, we should count that as 0 ways to make change.
3. If no coin value remains, we should count that as 0 ways to make change.

We can easily translate this description into a recursive function:

>>> def count_change(a, coin=50, next_func=next_coin):
        """Return the number of ways to change amount a using coin kinds."""
        if a == 0:
            return 1
        if a < 0 or coin == 0:
            return 0
        return count_change(a, next_func(coin)) + count_change(a - coin, coin)

>>> count_change(100)
292

In order to be as general as possible, the next_func parameter specifies the function to be used to iterate through a sequence of coins. As such, count_change is a higher-order function.

The count_change function generates a tree-recursive process with redundancies similar to those in our recursive implementation of fib. Unlike fib, however, it is not obvious how to design an iterative algorithm for counting change.