Chapter 2: Building Abstractions with Objects
Contents
2.1 Introduction
We concentrated in Chapter 1 on computational processes and on the role of functions in program design. We saw how to use primitive data (numbers) and primitive operations (arithmetic operations), how to form compound functions through composition and control, and how to create functional abstractions by giving names to processes. We also saw that higher-order functions enhance the power of our language by enabling us to manipulate, and thereby to reason, in terms of general methods of computation. This is much of the essence of programming.
This chapter focuses on data. Data allow us to represent and manipulate information about the world using the computational tools we have acquired so far. Programs without data structures may suffice for exploring mathematical properties. But real-world phenomena, such as documents, relationships, cities, and weather patterns, all have complex structure that is best represented using compound data types. With structured data, programs can simulate and reason about virtually any domain of human knowledge and experience. Due to the explosive growth of the Internet, a vast amount of structured information about the world is freely available to all of us online.
2.1.1 The Object Metaphor
In the beginning of this text, we distinguished between functions and data: functions performed operations and data were operated upon. When we included function values among our data, we acknowledged that data too can have behavior. Functions could be operated upon like data, but could also be called to perform computation.
In this text, objects will serve as our central programming metaphor for data values that also have behavior. Objects represent information, but also behave like the abstract concepts that they represent. The logic of how an object interacts with other objects is bundled along with the information that encodes the object's value. When an object is printed, it knows how to spell itself out as letters and numerals. If an object is composed of parts, it knows how to reveal those parts on demand. Objects are both information and processes, bundled together to represent the properties, interactions, and behaviors of complex things.
The object metaphor is implemented in Python through specialized object syntax and associated terminology, which we can introduce by example. A date is a kind of simple object.
>>> from datetime import date
The name date is bound to a class. A class represents a kind of object. Individual dates are called instances of that class, and they can be constructed by calling the class as a function on arguments that characterize the instance.
>>> today = date(2012, 9, 10)
While today was constructed from primitive numbers, it behaves like a date. For instance, subtracting it from another date will give a time difference, which we can display as a line of text by calling str.
>>> str(date(2012, 11, 30) - today) '81 days, 0:00:00'
Objects have attributes, which are named values that are part of the object. In Python, like many other programming languages, we use dot notation to designated an attribute of an object.
<expression> . <name>
Above, the <expression> evaluates to an object, and <name> is the name of an attribute for that object.
Unlike the names that we have considered so far, these attribute names are not available in the general environment. Instead, attribute names are particular to the object instance preceding the dot.
>>> today.year 2012
Objects also have methods, which are function-valued attributes. Metaphorically, we say that the object "knows" how to carry out those methods. By implementation, methods are functions that compute their results from both their arguments and their object. For example, The strftime method (a classic function name meant to evoke "string format of time") of today takes a single argument that specifies how to display a date (e.g., %A means that the day of the week should be spelled out in full).
>>> today.strftime('%A, %B %d')
'Monday, September 10'
Computing the return value of strftime requires two inputs: the string that describes the format of the output and the date information bundled into today. Date-specific logic is applied within this method to yield this result. We never stated that the 10th of September, 2012, was a Monday, but knowing one's weekday is part of what it means to be a date. By bundling behavior and information together, this Python object offers us a convincing, self-contained abstraction of a date.
Dot notation provides another form of combined expression in Python. Dot notation also has a well-defined evaluation procedure. However, developing a precise account of how dot notation is evaluated will have to wait until we introduce the full paradigm of object-oriented programming over the next several sections.
2.1.2 Native Data Types
Every object in Python has a type. The type function allows us to inspect the type of an object.
>>> type(today) <class 'datetime.date'>
So far, the types of objects we have used extensively are relatively few: numbers, functions, Booleans, and now dates. We also briefly encountered sets and strings in Chapter 1, but we will need to study those in more depth. There are many other kinds of objects --- sounds, images, locations, data connections, etc. --- most of which can be defined by the means of combination and abstraction that we develop in this chapter. Python has only a handful of primitive or native data types built into the language.
Native data types have the following properties:
- There are primitive expressions that evaluate to objects of these types, called literals.
- There are built-in functions, operators, and methods to manipulate these types of values.
As we have seen, numbers are native; numeric literals evaluate to numbers, and mathematical operators manipulate number objects.
>>> 12 + 3000000000000000000000000 3000000000000000000000012
In fact, Python includes three native numeric types: integers (int), real numbers (float), and complex numbers (complex).
>>> type(2) <class 'int'> >>> type(1.5) <class 'float'> >>> type(1+1j) <class 'complex'>
The name float comes from the way in which real numbers are represented in Python: a "floating point" representation. While the details of how numbers are represented is not a topic for this text, some high-level differences between int and float objects are important to know. In particular, int objects can only represent integers, but they represent them exactly, without any approximation. On the other hand, float objects can represent a wide range of fractional numbers, but not all rational numbers are representable. Nonetheless, float objects are often used to represent real and rational numbers approximately, up to some number of significant figures.
Further reading. The following sections introduce more of Python's native data types, focusing on the role they play in creating useful data abstractions. A chapter on native data types in the online book Dive Into Python 3 gives a pragmatic overview of all Python's native data types and how to use them effectively, including numerous usage examples and practical tips.
2.2 Data Abstraction
As we consider the wide set of things in the world that we would like to represent in our programs, we find that most of them have compound structure. A date has a year, a month, and a day; a geographic position has latitude and longitude coordinates. To represent positions, we would like our programming language to have the capacity to couple together a latitude and longitude to form a pair, a compound data value that our programs can manipulate as a single conceptual unit, but which also has two parts that can be considered individually.
The use of compound data enables us to increase the modularity of our programs. If we can manipulate geographic positions directly as objects in their own right, then we can separate the part of our program that deals with values per se from the details of how those values may be represented. The general technique of isolating the parts of a program that deal with how data are represented from the parts of a program that deal with how those data are manipulated is a powerful design methodology called data abstraction. Data abstraction makes programs much easier to design, maintain, and modify.
Data abstraction is similar in character to functional abstraction. When we create a functional abstraction, the details of how a function is implemented can be suppressed, and the particular function itself can be replaced by any other function with the same overall behavior. In other words, we can make an abstraction that separates the way the function is used from the details of how the function is implemented. Analogously, data abstraction is a methodology that enables us to isolate how a compound data object is used from the details of how it is constructed.
The basic idea of data abstraction is to structure programs so that they operate on abstract data. That is, our programs should use data in such a way as to make as few assumptions about the data as possible. At the same time, a concrete data representation is defined, independently of the programs that use the data. The interface between these two parts of our system will be a set of functions, called selectors and constructors, that implement the abstract data in terms of the concrete representation. To illustrate this technique, we will consider how to design a set of functions for manipulating rational numbers.
As you read the next few sections, keep in mind that most Python code written today uses very high-level abstract data types that are built into the language, like classes, dictionaries, and lists. Since we're building up an understanding of how these abstractions work, we can't use them yet ourselves. As a consequence, we will write some code that isn't typical of the typical way most Python programmers would implement these ideas in the language. What we write is instructive, however, because it demonstrates how these abstractions can be constructed! Remember that computer science isn't just about learning to use programming languages, but also understanding how they work.
2.2.1 Example: Arithmetic on Rational Numbers
Recall that a rational number is a ratio of integers, and rational numbers constitute an important sub-class of real numbers. A rational number like 1/3 or 17/29 is typically written as:
<numerator>/<denominator>
where both the <numerator> and <denominator> are placeholders for integer values. Both parts are needed to exactly characterize the value of the rational number.
Rational numbers are important in computer science because they, like integers, can be represented exactly. Irrational numbers (like pi or e or sqrt(2)) are instead approximated using a finite binary expansion. Thus, working with rational numbers should, in principle, allow us to avoid approximation errors in our arithmetic.
However, as soon as we actually divide the numerator by the denominator, we can be left with a truncated decimal approximation (a float).
>>> 1/3 0.3333333333333333
and the problems with this approximation appear when we start to conduct tests:
>>> 1/3 == 0.333333333333333300000 # Beware of approximations True
How computers approximate real numbers with finite-length decimal expansions is a topic for another class. The important idea here is that by representing rational numbers as ratios of integers, we avoid the approximation problem entirely. Hence, we would like to keep the numerator and denominator separate for the sake of precision, but treat them as a single unit.
We know from using functional abstractions that we can start programming productively before we have an implementation of some parts of our program. Let us begin by assuming that we already have a way of constructing a rational number from a numerator and a denominator. We also assume that, given a rational number, we have a way of extracting (or selecting) its numerator and its denominator. Let us further assume that the constructor and selectors are available as the following three functions:
- rational(n, d) returns the rational number with numerator n and denominator d.
- numer(x) returns the numerator of the rational number x.
- denom(x) returns the denominator of the rational number x.
We are using here a powerful strategy of synthesis: wishful thinking. We haven't yet said how a rational number is represented, or how the functions numer, denom, and rational should be implemented. Even so, if we did have these three functions, we could then add, multiply, and test equality of rational numbers by calling them:
>>> def add_rationals(x, y):
nx, dx = numer(x), denom(x)
ny, dy = numer(y), denom(y)
return rational(nx * dy + ny * dx, dx * dy)
>>> def mul_rationals(x, y):
return rational(numer(x) * numer(y), denom(x) * denom(y))
>>> def eq_rationals(x, y):
return numer(x) * denom(y) == numer(y) * denom(x)
Now we have the operations on rational numbers defined in terms of the selector functions numer and denom, and the constructor function rational, but we haven't yet defined these functions. What we need is some way to glue together a numerator and a denominator into a unit.
2.2.2 Pairs
To enable us to implement the concrete level of our data abstraction, Python provides a compound structure called a tuple, which can be constructed by separating values by commas. Although not strictly required, parentheses almost always surround tuples.
>>> (1, 2) (1, 2)
The elements of a tuple can be unpacked in two ways. The first way is via our familiar method of multiple assignment.
>>> pair = (1, 2) >>> pair (1, 2) >>> x, y = pair >>> x 1 >>> y 2
In fact, multiple assignment has been creating and unpacking tuples all along.
A second method for accessing the elements in a tuple is by the indexing operator, expressed using square brackets.
>>> pair[0] 1 >>> pair[1] 2
Tuples in Python (and sequences in most other programming languages) are 0-indexed, meaning that the index 0 picks out the first element, index 1 picks out the second, and so on. One intuition that underlies this indexing convention is that the index represents how far an element is offset from the beginning of the tuple.
The equivalent function for the element selection operator is called getitem, and it also uses 0-indexed positions to select elements from a tuple.
>>> from operator import getitem >>> getitem(pair, 0) 1
Tuples are native types, which means that there are built-in Python operators to manipulate them. We'll return to the full properties of tuples shortly. At present, we are only interested in how tuples can serve as the glue that implements abstract data types.
Representing Rational Numbers. Tuples offer a natural way to implement rational numbers as a pair of two integers: a numerator and a denominator. We can implement our constructor and selector functions for rational numbers by manipulating 2-element tuples.
>>> def rational(n, d):
return (n, d)
>>> def numer(x):
return getitem(x, 0)
>>> def denom(x):
return getitem(x, 1)
A function for printing rational numbers completes our implementation of this abstract data type.
>>> def rational_to_string(x):
"""Return a string 'n/d' for numerator n and denominator d."""
return '{0}/{1}'.format(numer(x), denom(x))
Together with the arithmetic operations we defined earlier, we can manipulate rational numbers with the functions we have defined.
>>> half = rational(1, 2) >>> rational_to_string(half) '1/2' >>> third = rational(1, 3) >>> rational_to_string(mul_rationals(half, third)) '1/6' >>> rational_to_string(add_rationals(third, third)) '6/9'
As the final example shows, our rational number implementation does not reduce rational numbers to lowest terms. We can remedy this by changing rational. If we have a function for computing the greatest common denominator of two integers, we can use it to reduce the numerator and the denominator to lowest terms before constructing the pair. As with many useful tools, such a function already exists in the Python Library.
>>> from fractions import gcd
>>> def rational(n, d):
g = gcd(n, d)
return (n//g, d//g)
The double slash operator, //, expresses integer division, which rounds down the fractional part of the result of division. Since we know that g divides both n and d evenly, integer division is exact in this case. Now we have
>>> rational_to_string(add_rationals(third, third)) '2/3'
as desired. This modification was accomplished by changing the constructor without changing any of the functions that implement the actual arithmetic operations.
Further reading. The rational_to_string implementation above uses format strings, which contain placeholders for values. The details of how to use format strings and the format method appear in the formatting strings section of Dive Into Python 3.
2.2.3 Abstraction Barriers
Before continuing with more examples of compound data and data abstraction, let us consider some of the issues raised by the rational number example. We defined operations in terms of a constructor rational and selectors numer and denom. In general, the underlying idea of data abstraction is to identify for each type of value a basic set of operations in terms of which all manipulations of values of that type will be expressed, and then to use only those operations in manipulating the data.
We can envision the structure of the rational number system as a series of layers.

The horizontal lines represent abstraction barriers that isolate different levels of the system. At each level, the barrier separates the functions (above) that use the data abstraction from the functions (below) that implement the data abstraction. Programs that use rational numbers manipulate them solely in terms of the their arithmetic functions: add_rationals, mul_rationals, and eq_rationals. These, in turn, are implemented solely in terms of the constructor and selectors rational, numer, and denom, which themselves are implemented in terms of tuples. The details of how tuples are implemented are irrelevant to the rest of the layers as long as tuples enable the implementation of the selectors and constructor.
At each layer, the functions within the box enforce the abstraction boundary because they are the only functions that depend upon both the representation above them (by their use) and the implementation below them (by their definitions). In this way, abstraction barriers are expressed as sets of functions.
Abstraction barriers provide many advantages. One advantage is that they makes programs much easier to maintain and to modify. The fewer functions that depend on a particular representation, the fewer changes are required when one wants to change that representation.
2.2.4 The Properties of Data
We began the rational-number implementation by implementing arithmetic operations in terms of three unspecified functions: rational, numer, and denom. At that point, we could think of the operations as being defined in terms of data objects --- numerators, denominators, and rational numbers --- whose behavior was specified by the latter three functions.
But what exactly is meant by data? It is not enough to say "whatever is implemented by the given selectors and constructors." We need to guarantee that these functions together specify the right behavior. That is, if we construct a rational number x from integers n and d, then it should be the case that numer(x)/denom(x) is equal to n/d.
In general, we can think of an abstract data type as defined by some collection of selectors and constructors, together with some behavior conditions. As long as the behavior conditions are met (such as the division property above), these functions constitute a valid representation of the data type.
This point of view can be applied to other data types as well, such as the two-element tuple that we used in order to implement rational numbers. We never actually said much about what a tuple was, only that the language supplied operators to create and manipulate tuples. We can now describe the behavior conditions of two-element tuples, also called pairs, that are relevant to the problem of representing rational numbers.
In order to implement rational numbers, we needed a form of glue for two integers, which had the following behavior:
- If a pair p was constructed from values x and y, then getitem_pair(p, 0) returns x, and getitem_pair(p, 1) returns y.
We can implement functions pair and getitem_pair that fulfill this description just as well as a tuple.
>>> def pair(x, y):
"""Return a function that behaves like a two-element tuple."""
def dispatch(m):
if m == 0:
return x
elif m == 1:
return y
return dispatch
>>> def getitem_pair(p, i):
"""Return the element at index i of pair p."""
return p(i)
With this implementation, we can create and manipulate pairs.
>>> p = pair(20, 12) >>> getitem_pair(p, 0) 20 >>> getitem_pair(p, 1) 12
This use of functions corresponds to nothing like our intuitive notion of what data should be. Nevertheless, these functions suffice to represent compound data in our programs.
The subtle point to notice is that the value returned by pair is a function called dispatch, which takes an argument m and returns either x or y. Then, getitem_pair calls this function to retrieve the appropriate value. We will return to the topic of dispatch functions several times throughout this chapter.
The point of exhibiting the functional representation of a pair is not that Python actually works this way (tuples are implemented more directly, for efficiency reasons) but that it could work this way. The functional representation, although obscure, is a perfectly adequate way to represent pairs, since it fulfills the only conditions that pairs need to fulfill. This example also demonstrates that the ability to manipulate functions as values automatically provides us the ability to represent compound data.
2.3 Sequences
A sequence is an ordered collection of data values. Unlike a pair, which has exactly two elements, a sequence can have an arbitrary (but finite) number of ordered elements.
The sequence is a powerful, fundamental abstraction in computer science. For example, if we have sequences, we can list every university in the world, or every student in every university. The sequence abstraction enables the thousands of data-driven programs that impact our lives every day.
A sequence is not a particular abstract data type, but instead a collection of behaviors that different types share. That is, there are many kinds of sequences, but they all share certain properties. In particular,
Length. A sequence has a finite length.
Element selection. A sequence has an element corresponding to any non-negative integer index less than its length, starting at 0 for the first element.
Unlike an abstract data type, we have not stated how to construct a sequence. The sequence abstraction is a collection of behaviors that does not fully specify a type (i.e., with constructors and selectors), but may be shared among several types. Sequences provide a layer of abstraction that may hide the details of exactly which sequence type is being manipulated by a particular program.
In this section, we introduce built-in Python types that implement the sequence abstraction. We then develop our own abstract data type that can implement the same abstraction.
2.3.1 Tuples
In fact, the tuple type that we introduced to form primitive pairs is itself a full sequence type. Tuples provide substantially more functionality than the pair abstract data type that we implemented functionally.
Tuples can have arbitrary length, and they exhibit the two principal behaviors of the sequence abstraction: length and element selection. Below, digits is a tuple with four elements.
>>> digits = (1, 8, 2, 8) >>> len(digits) 4 >>> digits[3] 8
Additionally, tuples can be added together and multiplied by integers. For tuples, addition and multiplication do not add or multiply elements, but instead combine and replicate the tuples themselves. That is, the add function in the operator module (and the + operator) returns a new tuple that is the conjunction of the added arguments. The mul function in operator (and the * operator) can take an integer k and a tuple and return a new tuple that consists of k copies of the tuple argument.
>>> (2, 7) + digits * 2 (2, 7, 1, 8, 2, 8, 1, 8, 2, 8)
Mapping. A powerful method of transforming one tuple into another is by applying a function to each element and collecting the results. This general form of computation is called mapping a function over a sequence, and corresponds to the built-in function map. The result of map is an object that is not itself a sequence, but can be converted into a sequence by calling tuple, the constructor function for tuples.
>>> alternates = (-1, 2, -3, 4, -5) >>> tuple(map(abs, alternates)) (1, 2, 3, 4, 5)
The map function is important because it relies on the sequence abstraction: we do not need to be concerned about the structure of the underlying tuple; only that we can access each one of its elements individually in order to pass it as an argument to the mapped function (abs, in this case).
Multiple assignment and return values. In Chapter 1, we saw that Python allows multiple names to be assigned in a single statement.
>>> from math import pi >>> radius = 10 >>> area, circumference = pi * radius * radius, 2 * pi * radius >>> area 314.1592653589793 >>> circumference 62.83185307179586
We can also return multiple values from a function.
>>> def divide_exact(n, d):
return n // d, n % d
>>> quotient, remainder = divide_exact(10, 3)
>>> quotient
3
>>> remainder
1
Python actually uses tuples to represent multiple values separated by commas. This is called tuple packing.
>>> digits = 1, 8, 2, 8 >>> digits (1, 8, 2, 8) >>> divide_exact(10, 3) (3, 1)
Using a tuple to assign to multiple names is called, as one might expect, tuple unpacking. The names may or may not be enclosed by parentheses.
>>> d0, d1, d2, d3 = digits >>> d2 2 >>> (quotient, remainder) = divide_exact(10, 3) >>> quotient 3 >>> remainder 1
Multiple assignment is just the combination of tuple packing and unpacking.
Arbitrary argument lists. Tuples can be used to define a function that takes in an arbitrary number of arguments, such as the built-in print function. We precede a parameter name with a * to indicate that an arbitrary number of arguments can be passed in for that parameter. Python automatically packs those arguments into a tuple and binds the parameter name to that tuple..
>>> def add_all(*args):
"""Compute the sum of all arguments."""
total, index = 0, 0
while index < len(args):
total = total + args[index]
index = index + 1
return total
>>> add_all(1, 3, 2) 6
In addition, we can use the * operator to unpack a tuple to pass its elements as separate arguments to a function call.
>>> pow(*(2, 3)) 8
As can be seen here, tuples are used to provide many of the features that we have been using in Python.
2.3.2 Sequence Iteration
Mapping is itself an instance of a general pattern of computation: iterating over all elements in a sequence. To map a function over a sequence, we do not just select a particular element, but each element in turn. This pattern is so common that Python has an additional control statement to process sequential data: the for statement.
Consider the problem of counting how many times a value appears in a sequence. We can implement a function to compute this count using a while loop.
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total, index = 0, 0
while index < len(s):
if s[index] == value:
total = total + 1
index = index + 1
return total
>>> count(digits, 8) 2
The Python for statement can simplify this function body by iterating over the element values directly, without introducing the name index at all. For example (pun intended), we can write:
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total = 0
for elem in s:
if elem == value:
total = total + 1
return total
>>> count(digits, 8) 2
A for statement consists of a single clause with the form:
for <name> in <expression>:
<suite>
A for statement is executed by the following procedure:
- Evaluate the header <expression>, which must yield an iterable value.
- For each element value in that sequence, in order:
- Bind <name> to that value in the local environment.
- Execute the <suite>.
Step 1 refers to an iterable value. Sequences are iterable, and their elements are considered in their sequential order. Python does include other iterable types, but we will focus on sequences for now; the general definition of the term "iterable" appears in the section on iterators in Chapter 4.
An important consequence of this evaluation procedure is that <name> will be bound to the last element of the sequence after the for statement is executed. The for loop introduces yet another way in which the local environment can be updated by a statement.
Sequence unpacking. A common pattern in programs is to have a sequence of elements that are themselves sequences, but all of a fixed length. For statements may include multiple names in their header to "unpack" each element sequence into its respective elements. For example, we may have a sequence of pairs (that is, two-element tuples),
>>> pairs = ((1, 2), (2, 2), (2, 3), (4, 4))
and wish to find the number of pairs that have the same first and second element.
>>> same_count = 0
The following for statement with two names in its header will bind each name x and y to the first and second elements in each pair, respectively.
>>> for x, y in pairs:
if x == y:
same_count = same_count + 1
>>> same_count 2
This pattern of binding multiple names to multiple values in a fixed-length sequence is called sequence unpacking; it is the same pattern that we see in assignment statements that bind multiple names to multiple values.
Ranges. A range is another built-in type of sequence in Python, which represents a range of integers. Ranges are created with the range function, which takes two integer arguments: the first number and one beyond the last number in the desired range.
>>> range(1, 10) # Includes 1, but not 10 range(1, 10)
Calling the tuple constructor on a range will create a tuple with the same elements as the range, so that the elements can be easily inspected.
>>> tuple(range(5, 8)) (5, 6, 7)
If only one argument is given, it is interpreted as one beyond the last value for a range that starts at 0.
>>> tuple(range(4)) (0, 1, 2, 3)
Ranges commonly appear as the expression in a for header to specify the number of times that the suite should be executed:
>>> total = 0
>>> for k in range(5, 8):
total = total + k
>>> total 18
A common convention is to use a single underscore character for the name in the for header if the name is unused in the suite:
>>> for _ in range(3):
print('Go Bears!')
Go Bears!
Go Bears!
Go Bears!
Note that an underscore is just another name in the environment as far as the interpreter is concerned, but has a conventional meaning among programmers that indicates the name will not appear in any expressions.
2.3.3 Sequence Abstraction
We have now introduced two types of native data types that implement the sequence abstraction: tuples and ranges. Both satisfy the conditions with which we began this section: length and element selection. Python includes two more behaviors of sequence types that extend the sequence abstraction.
Membership. A value can be tested for membership in a sequence. Python has two operators in and not in that evaluate to True or False depending on whether an element appears in a sequence.
>>> digits (1, 8, 2, 8) >>> 2 in digits True >>> 1828 not in digits True
All sequences also have methods called index and count, which return the index of (or count of) a value in a sequence.
Slicing. Sequences contain smaller sequences within them. We observed this property when developing our nested pairs implementation, which decomposed a sequence into its first element and the rest. A slice of a sequence is any span of the original sequence, designated by a pair of integers. As with the range constructor, the first integer indicates the starting index of the slice and the second indicates one beyond the ending index.
In Python, sequence slicing is expressed similarly to element selection, using square brackets. A colon separates the starting and ending indices. Any bound that is omitted is assumed to be an extreme value: 0 for the starting index, and the length of the sequence for the ending index.
>>> digits[0:2] (1, 8) >>> digits[1:] (8, 2, 8)
Enumerating these additional behaviors of the Python sequence abstraction gives us an opportunity to reflect upon what constitutes a useful data abstraction in general. The richness of an abstraction (that is, how many behaviors it includes) has consequences. For users of an abstraction, additional behaviors can be helpful. On the other hand, satisfying the requirements of a rich abstraction with a new data type can be challenging. To ensure that our implementation of recursive lists supported these additional behaviors would require some work. Another negative consequence of rich abstractions is that they take longer for users to learn.
Sequences have a rich abstraction because they are so ubiquitous in computing that learning a few complex behaviors is justified. In general, most user-defined abstractions should be kept as simple as possible.
Further reading. Slice notation admits a variety of special cases, such as negative starting values, ending values, and step sizes. A complete description appears in the subsection called slicing a list in Dive Into Python 3. In this chapter, we will only use the basic features described above.
2.3.4 Nested Pairs
For rational numbers, we paired together two integer objects using a two-element tuple, then showed that we could implement pairs just as well using functions. In that case, the elements of each pair we constructed were integers. However, like expressions, tuples can nest. Either element of a pair can itself be a pair, a property that holds true for either method of implementing a pair that we have seen: as a tuple or as a dispatch function.
We visualize pairs (two-element tuples) in environment diagrams using box-and-pointer notation. Pairs are depicted as boxes with two parts: the left part contains (an arrow to) the first element of the pair and the right part contains the second. Simple values such as numbers, strings, boolean values, and None appear within the box. Composite values, such as function values and other pairs, are connected by a pointer.
We can use recursion to process an arbitrary nesting of pairs. For example, let's write a function to compute the sum of all integer elements in a nesting of pairs and integers.
The sum_elems function computes the sum of integer elements in a nested pair by recursively computing the sums of its first and second elements and adding the results. The base case is when an element is an integer, in which case the sum is the integer itself.
Our ability to use tuples as the elements of other tuples provides a new means of combination in our programming language. We call the ability for tuples to nest in this way a closure property of the tuple data type. In general, a method for combining data values satisfies the closure property if the result of combination can itself be combined using the same method. Closure is the key to power in any means of combination because it permits us to create hierarchical structures --- structures made up of parts, which themselves are made up of parts, and so on. We will explore a range of hierarchical structures in Chapter 3. For now, we consider a particularly important structure.
2.3.5 Recursive Lists
We can use nested pairs to form lists of elements of arbitrary length, which will allow us to implement the sequence abstraction. The environment diagram below illustrates the structure of the recursive representation of a four-element list: 1, 2, 3, 4.
The list is represented by a chain of pairs. The first element of each pair is an element in the list, while the second is a pair that represents the rest of the list. The second element of the final pair is None, which indicates that the list has ended. This structure can be constructed using the nested tuple literal above.
This nested structure corresponds to a very useful way of thinking about sequences in general. A non-empty sequence can be decomposed into:
- its first element, and
- the rest of the sequence.
The rest of a sequence is itself a (possibly empty) sequence. We call this view of sequences recursive, because sequences contain other sequences as their second component.
Since our list representation is recursive, we will call it an rlist in our implementation, so as not to confuse it with the built-in list type in Python that we will discuss later. A recursive list can be constructed from a first element and the rest of the list. The value None represents an empty recursive list.
>>> empty_rlist = None
>>> def rlist(first, rest):
"""Construct a recursive list from its first element and the rest."""
return (first, rest)
>>> def first(s):
"""Return the first element of a recursive list s."""
return s[0]
>>> def rest(s):
"""Return the rest of the elements of a recursive list s."""
return s[1]
These two selectors, one constructor, and one constant together implement the recursive list abstract data type. The single behavior condition for a recursive list is that, like a pair, its constructor and selectors are inverse functions.
- If a recursive list s was constructed from element f and list r, then first(s) returns f, and rest(s) returns r.
We can use the constructor and selectors to manipulate recursive lists.
>>> counts = rlist(1, rlist(2, rlist(3, rlist(4, empty_rlist)))) >>> first(counts) 1 >>> rest(counts) (2, (3, (4, None)))
Recall that we were able to represent pairs using functions, and therefore we can represent recursive lists using functions as well.
The recursive list can store a sequence of values in order, but it does not yet implement the sequence abstraction. Using the abstract data type we have defined, we can implement the two behaviors that characterize a sequence: length and element selection.
>>> def len_rlist(s):
"""Return the length of recursive list s."""
length = 0
while s != empty_rlist:
s, length = rest(s), length + 1
return length
>>> def getitem_rlist(s, i):
"""Return the element at index i of recursive list s."""
while i > 0:
s, i = rest(s), i - 1
return first(s)
Now, we can manipulate a recursive list as a sequence:
>>> len_rlist(counts) 4 >>> getitem_rlist(counts, 1) # The second item has index 1 2
Both of these implementations are iterative. They peel away each layer of nested pair until the end of the list (in len_rlist) or the desired element (in getitem_rlist) is reached. We can also implement length and element selection using recursion.
>>> def len_rlist_recursive(s):
"""Return the length of a recursive list s."""
if s == empty_rlist:
return 0
return 1 + len_rlist_recursive(rest(s))
>>> def getitem_rlist_recursive(s, i):
"""Return the element at index i of recursive list s."""
if i == 0:
return first(s)
return getitem_rlist_recursive(rest(s), i - 1)
>>> len_rlist_recursive(counts) 4 >>> getitem_rlist_recursive(counts, 1) 2
These recursive implementations follow the chain of pairs until the end of the list (in len_rlist_recursive) or the desired element (in getitem_rlist_recursive) is reached.
Recursive lists can be manipulated using both iteration and recursion. In Chapter 3, however, we will see more complicated examples of recursive data structures that will require recursion to manipulate easily.
Let us return to the iterative way of implementing length and element selection. The series of environment diagrams below illustrate the iterative process by which getitem_rlist finds the element 2 at index 1 in the recursive list. Below, we have defined the rlist counts using Python primitives to simplify the diagrams. This implementation choice violate the abstraction barrier for the rlist data type, but allows us to inspect the computational process more easily for this example.
First, the function getitem_rlist is called, creating a local frame.
The expression in the while header evaluates to true, which causes the assignment statement in the while suite to be executed. The function rest returns the sublist starting with 2.
Next, the local name s will be updated to refer to the sub-list that begins with the second element of the original list. Evaluating the while header expression now yields a false value, and so Python evaluates the expression in the return statement on the final line of getitem_rlist.
This final environment diagram shows the local frame for the call to first, which contains the name s bound to that same sub-list. The first function selects the value 2 and returns it, which will also be returned from getitem_rlist.
This example demonstrates a common pattern of computation with recursive lists, where each step in an iteration operates on an increasingly shorter suffix of the original list. This incremental processing to find the length and elements of a recursive list does take some time to compute. (In Chapter 3, we will learn to characterize the computation time of iterative functions like these.) Python's built-in sequence types are implemented in a different way that does not have a large computational cost for computing the length of a sequence or retrieving its elements.
The way in which we construct recursive lists is rather verbose. Fortunately, Python provides a variety of built-in sequence types that provide both the versatility of the sequence abstraction, as well as convenient notation.
2.3.6 Strings
Text values are perhaps more fundamental to computer science than even numbers. As a case in point, Python programs are written and stored as text. The native data type for text in Python is called a string, and corresponds to the constructor str.
There are many details of how strings are represented, expressed, and manipulated in Python. Strings are another example of a rich abstraction, one which requires a substantial commitment on the part of the programmer to master. This section serves as a condensed introduction to essential string behaviors.
String literals can express arbitrary text, surrounded by either single or double quotation marks.
>>> 'I am string!' 'I am string!' >>> "I've got an apostrophe" "I've got an apostrophe" >>> '您好' '您好'
We have seen strings already in our code, as docstrings, in calls to print, and as error messages in assert statements.
Strings satisfy the two basic conditions of a sequence that we introduced at the beginning of this section: they have a length and they support element selection.
>>> city = 'Berkeley' >>> len(city) 8 >>> city[3] 'k'
The elements of a string are themselves strings that have only a single character. A character is any single letter of the alphabet, punctuation mark, or other symbol. Unlike many other programming languages, Python does not have a separate character type; any text is a string, and strings that represent single characters have a length of 1.
Like tuples, strings can also be combined via addition and multiplication.
>>> 'Berkeley' + ', CA' 'Berkeley, CA' >>> 'Shabu ' * 2 'Shabu Shabu '
Membership. The behavior of strings diverges from other sequence types in Python. The string abstraction does not conform to the full sequence abstraction that we described for tuples and ranges. In particular, the membership operator in applies to strings, but has an entirely different behavior than when it is applied to sequences. It matches substrings rather than elements.
>>> 'here' in "Where's Waldo?" True
Likewise, the count and index methods on strings take substrings as arguments, rather than single-character elements. The behavior of count is particularly nuanced; it counts the number of non-overlapping occurrences of a substring in a string.
>>> 'Mississippi'.count('i')
4
>>> 'Mississippi'.count('issi')
1
Multiline Literals. Strings aren't limited to a single line. Triple quotes delimit string literals that span multiple lines. We have used this triple quoting extensively already for docstrings.
>>> """The Zen of Python claims, Readability counts. Read more: import this.""" 'The Zen of Python\nclaims, "Readability counts."\nRead more: import this.'
In the printed result above, the \n (pronounced "backslash en") is a single element that represents a new line. Although it appears as two characters (backslash and "n"), it is considered a single character for the purposes of length and element selection.
String Coercion. A string can be created from any object in Python by calling the str constructor function with an object value as its argument. This feature of strings is useful for constructing descriptive strings from objects of various types.
>>> str(2) + ' is an element of ' + str(digits) '2 is an element of (1, 8, 2, 8)'
The mechanism by which a single str function can apply to any type of argument and return an appropriate value is the subject of the later section on generic functions.
Methods. The behavior of strings in Python is extremely productive because of a rich set of methods for returning string variants and searching for contents. A few of these methods are introduced below by example.
>>> '1234'.isnumeric()
True
>>> 'rOBERT dE nIRO'.swapcase()
'Robert De Niro'
>>> 'snakeyes'.upper().endswith('YES')
True
Further reading. Encoding text in computers is a complex topic. In this chapter, we will abstract away the details of how strings are represented. However, for many applications, the particular details of how strings are encoded by computers is essential knowledge. Sections 4.1-4.3 of Dive Into Python 3 provides a description of character encodings and Unicode.
2.3.7 Conventional Interfaces
In working with compound data, we've stressed how data abstraction permits us to design programs without becoming enmeshed in the details of data representations, and how abstraction preserves for us the flexibility to experiment with alternative representations. In this section, we introduce another powerful design principle for working with data structures --- the use of conventional interfaces.
A conventional interface is a data format that is shared across many modular components, which can be mixed and matched to perform data processing. For example, if we have several functions that all take a sequence as an argument and return a sequence as a value, then we can apply each to the output of the next in any order we choose. In this way, we can create a complex process by chaining together a pipeline of functions, each of which is simple and focused.
This section has a dual purpose: to introduce the idea of organizing a program around a conventional interface, and to demonstrate examples of modular sequence processing.
Consider these two problems, which appear at first to be related only in their use of sequences:
- Sum the even members of the first n Fibonacci numbers.
- List the letters in the acronym for a name, which includes the first letter of each capitalized word.
These problems are related because they can be decomposed into simple operations that take sequences as input and yield sequences as output. Moreover, those operations are instances of general methods of computation over sequences. Let's consider the first problem. It can be decomposed into the following steps:
enumerate map filter accumulate ----------- --- ------ ---------- naturals(n) fib iseven sum
The fib function below computes Fibonacci numbers (now updated from the definition in Chapter 1 with a for statement),
>>> def fib(k):
"""Compute the kth Fibonacci number."""
prev, curr = 1, 0 # curr is the first Fibonacci number.
for _ in range(k - 1):
prev, curr = curr, prev + curr
return curr
and a predicate iseven can be defined using the integer remainder operator, %.
>>> def iseven(n):
return n % 2 == 0
The functions map and filter are operations on sequences. We have already encountered map, which applies a function to each element in a sequence and collects the results. The filter function takes a sequence and returns those elements of a sequence for which a predicate is true. Both of these functions return intermediate objects, map and filter objects, which are iterable objects that can be converted into tuples or summed.
>>> nums = (5, 6, -7, -8, 9) >>> tuple(filter(iseven, nums)) (6, -8) >>> sum(map(abs, nums)) 35
Now we can implement even_fib, the solution to our first problem, in terms of map, filter, and sum.
>>> def sum_even_fibs(n):
"""Sum the even members of the first n Fibonacci numbers."""
return sum(filter(iseven, map(fib, range(1, n+1))))
>>> sum_even_fibs(20) 3382
Now, let's consider the second problem. It can also be decomposed as a pipeline of sequence operations that include map and filter:
enumerate filter map accumulate --------- ------ ----- ---------- words iscap first tuple
The words in a string can be enumerated via the split method of a string object, which by default splits on spaces.
>>> tuple('Spaces between words'.split())
('Spaces', 'between', 'words')
The first letter of a word can be retrieved using the selection operator, and a predicate that determines if a word is capitalized can be defined using the built-in predicate isupper.
>>> def first(s):
return s[0]
>>> def iscap(s):
return len(s) > 0 and s[0].isupper()
At this point, our acronym function can be defined via map and filter.
>>> def acronym(name):
"""Return a tuple of the letters that form the acronym for name."""
return tuple(map(first, filter(iscap, name.split())))
>>> acronym('University of California Berkeley Undergraduate Graphics Group')
('U', 'C', 'B', 'U', 'G', 'G')
These similar solutions to rather different problems show how to combine general components that operate on the conventional interface of a sequence using the general computational patterns of mapping, filtering, and accumulation. The sequence abstraction allows us to specify these solutions concisely.
Expressing programs as sequence operations helps us design programs that are modular. That is, our designs are constructed by combining relatively independent pieces, each of which transforms a sequence. In general, we can encourage modular design by providing a library of standard components together with a conventional interface for connecting the components in flexible ways.
Generator expressions. The Python language includes a second approach to processing sequences, called generator expressions. which provide similar functionality to map and filter, but may require fewer function definitions.
Generator expressions combine the ideas of filtering and mapping together into a single expression type with the following form:
<map expression> for <name> in <sequence expression> if <filter expression>
To evaluate a generator expression, Python evaluates the <sequence expression>, which must return an iterable value. Then, for each element in order, the element value is bound to <name>, the filter expression is evaluated, and if it yields a true value, the map expression is evaluated.
The result value of evaluating a generator expression is itself an iterable value. Accumulation functions like tuple, sum, max, and min can take this returned object as an argument.
>>> def acronym(name):
return tuple(w[0] for w in name.split() if iscap(w))
>>> def sum_even_fibs(n):
return sum(fib(k) for k in range(1, n+1) if fib(k) % 2 == 0)
Generator expressions are specialized syntax that utilizes the conventional interface of iterable values, such as sequences. These expressions subsume most of the functionality of map and filter, but avoid actually creating the function values that are applied (or, incidentally, creating the environment frames required to apply those functions).
Reduce. In our examples we used specific functions to accumulate results, either tuple or sum. Functional programming languages (including Python) include general higher-order accumulators that go by various names. Python includes reduce in the functools module, which applies a two-argument function cumulatively to the elements of a sequence from left to right, to reduce a sequence to a value. The following expression computes 5 factorial.
>>> from operator import mul >>> from functools import reduce >>> reduce(mul, (1, 2, 3, 4, 5)) 120
Using this more general form of accumulation, we can also compute the product of even Fibonacci numbers, in addition to the sum, using sequences as a conventional interface.
>>> def product_even_fibs(n):
"""Return the product of the first n even Fibonacci numbers, except 0."""
return reduce(mul, filter(iseven, map(fib, range(2, n+1))))
>>> product_even_fibs(20) 123476336640
The combination of higher order procedures corresponding to map, filter, and reduce will appear again in Chapter 4, when we consider methods for distributing computation across multiple computers.
2.4 Mutable Data
We have seen how abstraction is vital in helping us to cope with the complexity of large systems. Effective program synthesis also requires organizational principles that can guide us in formulating the overall design of a program. In particular, we need strategies to help us structure large systems so that they will be modular, that is, so that they can be divided "naturally" into coherent parts that can be separately developed and maintained.
One powerful technique for creating modular programs is to introduce new kinds of data that may change state over time. In this way, a single data object can represent something that evolves independently of the rest of the program. The behavior of a changing object may be influenced by its history, just like an entity in the world. Adding state to data is an essential ingredient of our final destination in this chapter: object-oriented programming.
The native data types we have introduced so far --- numbers, Booleans, tuples, ranges, and strings --- are all types of immutable objects. While names may change bindings to different values in the environment during the course of execution, the values themselves do not change. Mutable objects (also called mutable values) can change throughout the execution of a program.
2.4.1 Lists
The list is Python's most useful and flexible sequence type. A list is similar to a tuple, but it is mutable: Method calls and assignment statements can change the contents of a list.
We can introduce many list modification operations through an example that illustrates the history of playing cards (drastically simplified). Comments in the examples describe the effect of each method invocation.
Playing cards were invented in China, perhaps around the 9th century. An early deck had three suits, which corresponded to denominations of money.
>>> chinese_suits = ['coin', 'string', 'myriad'] # A list literal >>> suits = chinese_suits # Two names refer to the same list
As cards migrated to Europe (perhaps through Egypt), only the suit of coins remained in Spanish decks (oro).
>>> suits.pop() # Remove and return the final element
'myriad'
>>> suits.remove('string') # Remove the first element that equals the argument
Three more suits were added (they evolved in name and design over time),
>>> suits.append('cup') # Add an element to the end
>>> suits.extend(['sword', 'club']) # Add all elements of a list to the end
and Italians called swords spades.
>>> suits[2] = 'spade' # Replace an element
giving the suits of a traditional Italian deck of cards.
>>> suits ['coin', 'cup', 'spade', 'club']
The French variant that we use today in the U.S. changes the first two:
>>> suits[0:2] = ['heart', 'diamond'] # Replace a slice >>> suits ['heart', 'diamond', 'spade', 'club']
Methods also exist for inserting, sorting, and reversing lists. All of these mutation operations change the value of the list; they do not create new list objects.
Sharing and Identity. Because we have been changing a single list rather than creating new lists, the object bound to the name chinese_suits has also changed, because it is the same list object that was bound to suits!
>>> chinese_suits # This name co-refers with "suits" to the same list ['heart', 'diamond', 'spade', 'club']
This behavior is new. Previously, if a name did not appear in a statement, then its value would not be affected by that statement. With mutable data, methods called on one name can affect another name at the same time.
The environment diagram for this example shows how the value bound to chinese is changed by statements involving only suits. Step through each line of the following example to observe these changes.
Lists can be copied using the list constructor function. Changes to one list do not affect another, unless they share structure.
>>> nest = list(suits) # Bind "nest" to a second list with the same elements >>> nest[0] = suits # Create a nested list
According to this environment, changing the list referenced by suits will affect the nested list that is the first element of nest, but not the other elements.
>>> suits.insert(2, 'Joker') # Insert an element at index 2, shifting the rest >>> nest [['heart', 'diamond', 'Joker', 'spade', 'club'], 'diamond', 'spade', 'club']
And likewise, undoing this change in the first element of nest will change suit as well.
>>> nest[0].pop(2) 'Joker' >>> suits ['heart', 'diamond', 'spade', 'club']
Stepping through this example line by line will show the representation of a nested list.
Because two lists may have the same contents but in fact be different lists, we require a means to test whether two objects are the same. Python includes two comparison operators, called is and is not, that test whether two expressions in fact evaluate to the identical object. Two objects are identical if they are equal in their current value, and any change to one will always be reflected in the other. Identity is a stronger condition than equality.
>>> suits is nest[0] True >>> suits is ['heart', 'diamond', 'spade', 'club'] False >>> suits == ['heart', 'diamond', 'spade', 'club'] True
The final two comparisons illustrate the difference between is and ==. The former checks for identity, while the latter checks for the equality of contents.
List comprehensions. A list comprehension uses an extended syntax for creating lists, analogous to the syntax of generator expressions.
For example, the unicodedata module tracks the official names of every character in the Unicode alphabet. We can look up the characters corresponding to names, including those for card suits.
>>> from unicodedata import lookup
>>> [lookup('WHITE ' + s.upper() + ' SUIT') for s in suits]
['♡', '♢', '♤', '♧']
List comprehensions reinforce the paradigm of data processing using the conventional interface of sequences, as list is a sequence data type.
2.4.2 Dictionaries
Dictionaries are Python's built-in data type for storing and manipulating correspondence relationships. A dictionary contains key-value pairs, where both the keys and values are objects. The purpose of a dictionary is to provide an abstraction for storing and retrieving values that are indexed not by consecutive integers, but by descriptive keys.
Strings commonly serve as keys, because strings are our conventional representation for names of things. This dictionary literal gives the values of various Roman numerals.
>>> numerals = {'I': 1.0, 'V': 5, 'X': 10}
Looking up values by their keys uses the element selection operator that we previously applied to sequences.
>>> numerals['X'] 10
A dictionary can have at most one value for each key. Adding new key-value pairs and changing the existing value for a key can both be achieved with assignment statements.
>>> numerals['I'] = 1
>>> numerals['L'] = 50
>>> numerals
{'I': 1, 'X': 10, 'L': 50, 'V': 5}
Notice that 'L' was not added to the end of the output above. Dictionaries are unordered collections of key-value pairs. When we print a dictionary, the keys and values are rendered in some order, but as users of the language we cannot predict what that order will be.
Dictionaries can appear in environment diagrams as well.
The dictionary abstraction also supports various methods of iterating of the contents of the dictionary as a whole. The methods keys, values, and items all return iterable values.
>>> sum(numerals.values()) 66
A list of key-value pairs can be converted into a dictionary by calling the dict constructor function.
>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}
Dictionaries do have some restrictions:
- A key of a dictionary cannot be an object of a mutable built-in type.
- There can be at most one value for a given key.
This first restriction is tied to the underlying implementation of dictionaries in Python. The details of this implementation are not a topic of this text. Intuitively, consider that the key tells Python where to find that key-value pair in memory; if the key changes, the location of the pair may be lost.
The second restriction is a consequence of the dictionary abstraction, which is designed to store and retrieve values for keys. We can only retrieve the value for a key if at most one such value exists in the dictionary.
A useful method implemented by dictionaries is get, which returns either the value for a key, if the key is present, or a default value. The arguments to get are the key and the default value.
>>> numerals.get('A', 0)
0
>>> numerals.get('V', 0)
5
Dictionaries also have a comprehension syntax analogous to those of lists and generator expressions. Evaluating a dictionary comprehension yields a new dictionary object.
>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}
2.4.3 Local State
Lists and dictionaries have local state: they are changing values that have some particular contents at any point in the execution of a program. The word state implies an evolving process in which that state may change.
Functions can also have local state. For instance, let us define a function that models the process of withdrawing money from a bank account. We will create a function called withdraw, which takes as its argument an amount to be withdrawn. If there is enough money in the account to accommodate the withdrawal, then withdraw will return the balance remaining after the withdrawal. Otherwise, withdraw will return the message 'Insufficient funds'. For example, if we begin with $100 in the account, we would like to obtain the following sequence of return values by calling withdraw:
>>> withdraw(25) 75 >>> withdraw(25) 50 >>> withdraw(60) 'Insufficient funds' >>> withdraw(15) 35
Above, the expression withdraw(25), evaluated twice, yields different values. Thus, this user-defined function is non-pure. Calling the function not only returns a value, but also has the side effect of changing the function in some way, so that the next call with the same argument will return a different result. This side effect is a result of withdraw making a change to a name-value binding outside of its local environment frame.
For withdraw to make sense, it must be created with an initial account balance. The function make_withdraw is a higher-order function that takes a starting balance as an argument. The function withdraw is its return value.
>>> withdraw = make_withdraw(100)
An implementation of make_withdraw requires a new kind of statement: a nonlocal statement. When we call make_withdraw, we bind the name balance to the initial amount. We then define and return a local function, withdraw, which updates and returns the value of balance when called.
>>> def make_withdraw(balance):
"""Return a withdraw function that draws down balance with each call."""
def withdraw(amount):
nonlocal balance # Declare the name "balance" nonlocal
if amount > balance:
return 'Insufficient funds'
balance = balance - amount # Re-bind the existing balance name
return balance
return withdraw
The novel part of this implementation is the nonlocal statement, which mandates that whenever we change the binding of the name balance, the binding is changed in the first frame in which balance is already bound. Recall that without the nonlocal statement, an assignment statement would always bind a name in the first frame of the environment. The nonlocal statement indicates that the name appears somewhere in the environment other than the first (local) frame or the last (global) frame.
The following environment diagrams illustrate the effects of multiple calls to a function created by make_withdraw.
The first def statement has the usual effect: it creates a new user-defined function and binds the name make_withdraw to that function in the global frame. The subsequent call to make_withdraw creates and returns a locally defined function withdraw. The name balance is bound in the parent frame of this function. Crucially, there will only be this single binding for the name balance throughout the rest of this example.
Next, we evaluate an expression that calls this function, bound to the name wd, on an amount 5. The body of withdraw is executed in a new environment that extends the environment in which withdraw was defined. Tracing the effect of evaluating withdraw illustrates the effect of a nonlocal statement in Python: a name outside of the first local frame can be changed by an assignment statement.
The nonlocal statement changes all of the remaining assignment statements in the definition of withdraw. After executing nonlocal balance, any assignment statement with balance on the left-hand side of = will not bind balance in the first frame of the current environment. Instead, it will find the first frame in which balance was already defined and re-bind the name in that frame. If balance has not previously been bound to a value, then the nonlocal statement will give an error.
By virtue of changing the binding for balance, we have changed the withdraw function as well. The next time it is called, the name balance will evaluate to 15 instead of 20. Hence, when we call withdraw a second time, we see that its return value is 12 and not 17. The change to balance from the first call affects the result of the second call.
The second call to withdraw does create a second local frame, as usual. However, both withdraw frames have the same parent. That is, they both extend the environment for make_withdraw, which contains the binding for balance. Hence, they share that particular name binding. Calling withdraw has the side effect of altering the environment that will be extended by future calls to withdraw. The nonlocal statement allows withdraw to change a name binding in the make_withdraw frame.
Ever since we first encountered nested def statements, we have observed that a locally defined function can look up names outside of its local frames. No nonlocal statement is required to access a non-local name. By contrast, only after a nonlocal statement can a function change the binding of names in these frames.
Practical Guidance. By introducing nonlocal statements, we have created a dual role for assignment statements. Either they change local bindings, or they change nonlocal bindings. In fact, assignment statements already had a dual role: they either created new bindings or re-bound existing names. Assignment can also change the contents of lists and dictionaries. The many roles of Python assignment can obscure the effects of executing an assignment statement. It is up to you as a programmer to document your code clearly so that the effects of assignment can be understood by others.
Python Particulars. This pattern of non-local assignment is a general feature of programming languages with higher-order functions and lexical scope. Most other languages do not require a nonlocal statement at all. Instead, non-local assignment is often the default behavior of assignment statements.
Python also has an unusual restriction regarding the lookup of names: within the body of a function, all instances of a name must refer to the same frame. As a result, Python cannot look up the value of a name in a non-local frame, then bind that same name in the local frame, because the same name would be accessed in two different frames in the same function. This restriction allows Python to pre-compute which frame contains each name before executing the body of a function. When this restriction is violated, a confusing error message results. To demonstrate, the make_withdraw example is repeated below with the nonlocal statement removed.
This UnboundLocalError appears because balance is assigned locally in line 5, and so Python assumes that all references to balance must appear in the local frame as well. This error occurs before line 5 is ever executed, implying that Python has considered line 5 in some way before executing line 3. As we study interpreter design, we will see that pre-computing facts about a function body before executing it is quite common. In this case, Python's pre-processing restricted the frame in which balance could appear, and thus prevented the name from being found. Adding a nonlocal statement corrects this error. The nonlocal statement did not exist in Python 2.
2.4.4 The Benefits of Non-Local Assignment
Non-local assignment is an important step on our path to viewing a program as a collection of independent and autonomous objects, which interact with each other but each manage their own internal state.
In particular, non-local assignment has given us the ability to maintain some state that is local to a function, but evolves over successive calls to that function. The balance associated with a particular withdraw function is shared among all calls to that function. However, the binding for balance associated with an instance of withdraw is inaccessible to the rest of the program. Only wd is associated with the frame for make_withdraw in which it was defined. If make_withdraw is called again, then it will create a separate frame with a separate binding for balance.
We can extend our example to illustrate this point. A second call to make_withdraw returns a second withdraw function that has a different parent. We bind this second function to the name wd2 in the global frame.
Now, we see that there are in fact two bindings for the name balance in two different frames, and each withdraw function has a different parent. The name wd is bound to a function with a balance of 20, while wd2 is bound to a different function with a balance of 7.
Calling wd2 changes the binding of its non-local balance name, but does not affect the function bound to the name withdraw. A future call to wd is unaffected by the changing balance of wd2; its balance is still 20.
In this way, each instance of withdraw maintains its own balance state, but that state is inaccessible to any other function in the program. Viewing this situation at a higher level, we have created an abstraction of a bank account that manages its own internals but behaves in a way that models accounts in the world: it changes over time based on its own history of withdrawal requests.
2.4.5 The Cost of Non-Local Assignment
Our environment model of computation cleanly extends to explain the effects of non-local assignment. However, non-local assignment introduces some important nuances in the way we think about names and values.
Previously, our values did not change; only our names and bindings changed. When two names a and b were both bound to the value 4, it did not matter whether they were bound to the same 4 or different 4's. As far as we could tell, there was only one 4 object that never changed.
However, functions with state do not behave this way. When two names wd and wd2 are both bound to a withdraw function, it does matter whether they are bound to the same function or different instances of that function. Consider the following example, which contrasts the one we just analyzed. In this case, calling the function named by wd2 did change the value of the function named by wd, because both names refer to the same function.
It is not unusual for two names to co-refer to the same value in the world, and so it is in our programs. But, as values change over time, we must be very careful to understand the effect of a change on other names that might refer to those values.
The key to correctly analyzing code with non-local assignment is to remember that only function calls can introduce new frames. Assignment statements always change bindings in existing frames. In this case, unless make_withdraw is called twice, there can be only one binding for balance.
Sameness and change. These subtleties arise because, by introducing non-pure functions that change the non-local environment, we have changed the nature of expressions. An expression that contains only pure function calls is referentially transparent; its value does not change if we substitute one of its subexpression with the value of that subexpression.
Re-binding operations violate the conditions of referential transparency because they do more than return a value; they change the environment. When we introduce arbitrary re-binding, we encounter a thorny epistemological issue: what it means for two values to be the same. In our environment model of computation, two separately defined functions are not the same, because changes to one may not be reflected in the other.
In general, so long as we never modify data objects, we can regard a compound data object to be precisely the totality of its pieces. For example, a rational number is determined by giving its numerator and its denominator. But this view is no longer valid in the presence of change, where a compound data object has an "identity" that is something different from the pieces of which it is composed. A bank account is still "the same" bank account even if we change the balance by making a withdrawal; conversely, we could have two bank accounts that happen to have the same balance, but are different objects.
Despite the complications it introduces, non-local assignment is a powerful tool for creating modular programs. Different parts of a program, which correspond to different environment frames, can evolve separately throughout program execution. Moreover, using functions with local state, we are able to implement mutable data types. In fact, we can implement abstract data types that are equivalent to the built-in list and dict types introduced above.
2.4.6 Implementing Lists and Dictionaries
Lists are sequences, like tuples. The Python language does not give us access to the implementation of lists, only to the sequence abstraction and the mutation methods we have introduced in this section. To overcome this language-enforced abstraction barrier, we can develop a functional implementation of lists, again using a recursive representation. This section also has a second purpose: to further our understanding of dispatch functions.
We will implement a list as a function that has a recursive list as its local state. Lists need to have an identity, like any mutable value. In particular, we cannot use None to represent an empty mutable list, because two empty lists are not identical values (e.g., appending to one does not append to the other), but None is None. On the other hand, two different functions that each have empty_rlist as their local state will suffice to distinguish two empty lists.
Our mutable list is a dispatch function, just as our functional implementation of a pair was a dispatch function. It checks the input "message" against known messages and takes an appropriate action for each different input. Our mutable list responds to five different messages. The first two implement the behaviors of the sequence abstraction. The next two add or remove the first element of the list. The final message returns a string representation of the whole list contents.
>>> def mutable_rlist():
"""Return a functional implementation of a mutable recursive list."""
contents = empty_rlist
def dispatch(message, value=None):
nonlocal contents
if message == 'len':
return len_rlist(contents)
elif message == 'getitem':
return getitem_rlist(contents, value)
elif message == 'push_first':
contents = rlist(value, contents)
elif message == 'pop_first':
f = first(contents)
contents = rest(contents)
return f
elif message == 'str':
return str(contents)
return dispatch
We can also add a convenience function to construct a functionally implemented recursive list from any built-in sequence, simply by adding each element in reverse order.
>>> def to_mutable_rlist(source):
"""Return a functional list with the same contents as source."""
s = mutable_rlist()
for element in reversed(source):
s('push_first', element)
return s
In the definition above, the function reversed takes and returns an iterable value; it is another example of a function that uses the conventional interface of sequences.
At this point, we can construct a functionally implemented lists. Note that the list itself is a function.
>>> s = to_mutable_rlist(suits)
>>> type(s)
<class 'function'>
>>> s('str')
"('heart', ('diamond', ('spade', ('club', None))))"
In addition, we can pass messages to the list s that change its contents, for instance removing the first element.
>>> s('pop_first')
'heart'
>>> s('str')
"('diamond', ('spade', ('club', None)))"
In principle, the operations push_first and pop_first suffice to make arbitrary changes to a list. We can always empty out the list entirely and then replace its old contents with the desired result.
Message passing. Given some time, we could implement the many useful mutation operations of Python lists, such as extend and insert. We would have a choice: we could implement them all as functions, which use the existing messages pop_first and push_first to make all changes. Alternatively, we could add additional elif clauses to the body of dispatch, each checking for a message (e.g., 'extend') and applying the appropriate change to contents directly.
This second approach, which encapsulates the logic for all operations on a data value within one function that responds to different messages, is called message passing. A program that uses message passing defines dispatch functions, each of which may have local state, and organizes computation by passing "messages" as the first argument to those functions. The messages are strings that correspond to particular behaviors.
One could imagine that enumerating all of these messages by name in the body of dispatch would become tedious and prone to error. Python dictionaries, introduced in the next section, provide a data type that will help us manage the mapping between messages and operations.
Implementing Dictionaries. We can implement an abstract data type that conforms to the dictionary abstraction as a list of records, each of which is a two-element list consisting of a key and the associated value.
>>> def dictionary():
"""Return a functional implementation of a dictionary."""
records = []
def getitem(key):
for k, v in records:
if k == key:
return v
def setitem(key, value):
for item in records:
if item[0] == key:
item[1] = value
return
records.append([key, value])
def dispatch(message, key=None, value=None):
if message == 'getitem':
return getitem(key)
elif message == 'setitem':
setitem(key, value)
elif message == 'keys':
return tuple(k for k, _ in records)
elif message == 'values':
return tuple(v for _, v in records)
return dispatch
Again, we use the message passing method to organize our implementation. We have supported four messages: getitem, setitem, keys, and values. To look up a value for a key, we iterate through the records to find a matching key. To insert a value for a key, we iterate through the records to see if there is already a record with that key. If not, we form a new record. If there already is a record with this key, we set the value of the record to the designated new value.
We can now use our implementation to store and retrieve values.
>>> d = dictionary()
>>> d('setitem', 3, 9)
>>> d('setitem', 4, 16)
>>> d('getitem', 3)
9
>>> d('getitem', 4)
16
>>> d('keys')
(3, 4)
>>> d('values')
(9, 16)
This implementation of a dictionary is not optimized for fast record lookup, because each response to the message 'getitem' must iterate through the entire list of records. The built-in dictionary type is considerably more efficient.
2.4.7 Dispatch Dictionaries
The dispatch function is a general method for implementing a message passing interface for an abstract data type. To implement message dispatch, we have thus far used a large conditional statement to look up function values using message strings.
The built-in dictionary data type provides a general method for looking up a value for a key. Instead of using dispatch functions to implement abstract data types, we can use dictionaries with string keys.
The mutable account data type below is implemented as a dictionary. It has a constructor account and selector check_balance, as well as functions to deposit or withdraw funds. Moreover, the local state of the account is stored in the dictionary alongside the functions that implement its behavior.
The name dispatch within the body of the account constructor is bound to a dictionary that contains the messages accepted by an account as keys. The balance is a number, while the messages deposit and withdraw are bound to functions. These functions have access to the dispatch dictionary, and so they can read and change the balance. By storing the balance in the dispatch dictionary rather than in the account frame directly, we avoid the need for nonlocal statements in deposit and withdraw.
The operators += and -= are shorthand in Python (and many other languages) for combined lookup and re-assignment. The last two lines below are equivalent.
>>> a = 2 >>> a = a + 1 >>> a += 1
2.4.8 Bonus Material: Propagating Constraints
Mutable data allows us to simulate systems with change, but also allows us to build new kinds of abstractions. In this extended example, we combine nonlocal assignment, lists, and dictionaries to build a constraint-based system that supports computation in multiple directions. Expressing programs as constraints is a type of declarative programming, in which a programmer declares the structure of a problem to be solved, but abstracts away the details of exactly how the solution to the problem is computed.
Computer programs are traditionally organized as one-directional computations, which perform operations on pre-specified arguments to produce desired outputs. On the other hand, we often want to model systems in terms of relations among quantities. For example, we previously considered the ideal gas law, which relates the pressure (p), volume (v), quantity (n), and temperature (t) of an ideal gas via Boltzmann's constant (k):
p * v = n * k * t
Such an equation is not one-directional. Given any four of the quantities, we can use this equation to compute the fifth. Yet translating the equation into a traditional computer language would force us to choose one of the quantities to be computed in terms of the other four. Thus, a function for computing the pressure could not be used to compute the temperature, even though the computations of both quantities arise from the same equation.
In this section, we sketch the design of a general model of linear relationships. We define primitive constraints that hold between quantities, such as an adder(a, b, c) constraint that enforces the mathematical relationship a + b = c.
We also define a means of combination, so that primitive constraints can be combined to express more complex relations. In this way, our program resembles a programming language. We combine constraints by constructing a network in which constraints are joined by connectors. A connector is an object that "holds" a value and may participate in one or more constraints.
For example, we know that the relationship between Fahrenheit and Celsius temperatures is:
9 * c = 5 * (f - 32)
This equation is a complex constraint between c and f. Such a constraint can be thought of as a network consisting of primitive adder, multiplier, and constant constraints.
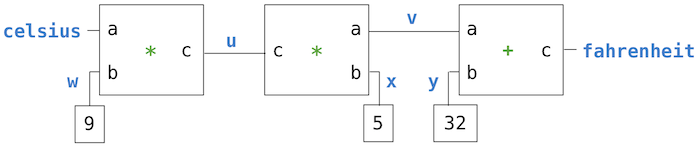
In this figure, we see on the left a multiplier box with three terminals, labeled a, b, and c. These connect the multiplier to the rest of the network as follows: The a terminal is linked to a connector celsius, which will hold the Celsius temperature. The b terminal is linked to a connector w, which is also linked to a constant box that holds 9. The c terminal, which the multiplier box constrains to be the product of a and b, is linked to the c terminal of another multiplier box, whose b is connected to a constant 5 and whose a is connected to one of the terms in the sum constraint.
Computation by such a network proceeds as follows: When a connector is given a value (by the user or by a constraint box to which it is linked), it awakens all of its associated constraints (except for the constraint that just awakened it) to inform them that it has a value. Each awakened constraint box then polls its connectors to see if there is enough information to determine a value for a connector. If so, the box sets that connector, which then awakens all of its associated constraints, and so on. For instance, in conversion between Celsius and Fahrenheit, w, x, and y are immediately set by the constant boxes to 9, 5, and 32, respectively. The connectors awaken the multipliers and the adder, which determine that there is not enough information to proceed. If the user (or some other part of the network) sets the celsius connector to a value (say 25), the leftmost multiplier will be awakened, and it will set u to 25 * 9 = 225. Then u awakens the second multiplier, which sets v to 45, and v awakens the adder, which sets the fahrenheit connector to 77.
Using the Constraint System. To use the constraint system to carry out the temperature computation outlined above, we first create two named connectors, celsius and fahrenheit, by calling the connector constructor.
>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')
Then, we link these connectors into a network that mirrors the figure above. The function converter assembles the various connectors and constraints in the network.
>>> def converter(c, f):
"""Connect c to f with constraints to convert from Celsius to Fahrenheit."""
u, v, w, x, y = [connector() for _ in range(5)]
multiplier(c, w, u)
multiplier(v, x, u)
adder(v, y, f)
constant(w, 9)
constant(x, 5)
constant(y, 32)
>>> converter(celsius, fahrenheit)
We will use a message passing system to coordinate constraints and connectors. Constraints are dictionaries that do not hold local states themselves. Their responses to messages are non-pure functions that change the connectors that they constrain.
Connectors are dictionaries that hold a current value and respond to messages that manipulate that value. Constraints will not change the value of connectors directly, but instead will do so by sending messages, so that the connector can notify other constraints in response to the change. In this way, a connector represents a number, but also encapsulates connector behavior.
One message we can send to a connector is to set its value. Here, we (the 'user') set the value of celsius to 25.
>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0
Not only does the value of celsius change to 25, but its value propagates through the network, and so the value of fahrenheit is changed as well. These changes are printed because we named these two connectors when we constructed them.
Now we can try to set fahrenheit to a new value, say 212.
>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212
The connector complains that it has sensed a contradiction: Its value is 77.0, and someone is trying to set it to 212. If we really want to reuse the network with new values, we can tell celsius to forget its old value:
>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten
The connector celsius finds that the user, who set its value originally, is now retracting that value, so celsius agrees to lose its value, and it informs the rest of the network of this fact. This information eventually propagates to fahrenheit, which now finds that it has no reason for continuing to believe that its own value is 77. Thus, it also gives up its value.
Now that fahrenheit has no value, we are free to set it to 212:
>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0
This new value, when propagated through the network, forces celsius to have a value of 100. We have used the very same network to compute celsius given fahrenheit and to compute fahrenheit given celsius. This non-directionality of computation is the distinguishing feature of constraint-based systems.
Implementing the Constraint System. As we have seen, connectors are dictionaries that map message names to function and data values. We will implement connectors that respond to the following messages:
- connector['set_val'](source, value) indicates that the source is requesting the connector to set its current value to value.
- connector['has_val']() returns whether the connector already has a value.
- connector['val'] is the current value of the connector.
- connector['forget'](source) tells the connector that the source is requesting it to forget its value.
- connector['connect'](source) tells the connector to participate in a new constraint, the source.
Constraints are also dictionaries, which receive information from connectors by means of two messages:
- constraint['new_val']() indicates that some connector that is connected to the constraint has a new value.
- constraint['forget']() indicates that some connector that is connected to the constraint has forgotten its value.
When constraints receive these messages, they propagate them appropriately to other connectors.
The adder function constructs an adder constraint over three connectors, where the first two must add to the third: a + b = c. To support multidirectional constraint propagation, the adder must also specify that it subtracts a from c to get b and likewise subtracts b from c to get a.
>>> from operator import add, sub
>>> def adder(a, b, c):
"""The constraint that a + b = c."""
return make_ternary_constraint(a, b, c, add, sub, sub)
We would like to implement a generic ternary (three-way) constraint, which uses the three connectors and three functions from adder to create a constraint that accepts new_val and forget messages. The response to messages are local functions, which are placed in a dictionary called constraint.
>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
"""The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b) = a."""
def new_value():
av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
if av and bv:
c['set_val'](constraint, ab(a['val'], b['val']))
elif av and cv:
b['set_val'](constraint, ca(c['val'], a['val']))
elif bv and cv:
a['set_val'](constraint, cb(c['val'], b['val']))
def forget_value():
for connector in (a, b, c):
connector['forget'](constraint)
constraint = {'new_val': new_value, 'forget': forget_value}
for connector in (a, b, c):
connector['connect'](constraint)
return constraint
The dictionary called constraint is a dispatch dictionary, but also the constraint object itself. It responds to the two messages that constraints receive, but is also passed as the source argument in calls to its connectors.
The constraint's local function new_value is called whenever the constraint is informed that one of its connectors has a value. This function first checks to see if both a and b have values. If so, it tells c to set its value to the return value of function ab, which is add in the case of an adder. The constraint passes itself (constraint) as the source argument of the connector, which is the adder object. If a and b do not both have values, then the constraint checks a and c, and so on.
If the constraint is informed that one of its connectors has forgotten its value, it requests that all of its connectors now forget their values. (Only those values that were set by this constraint are actually lost.)
A multiplier is very similar to an adder.
>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
"""The constraint that a * b = c."""
return make_ternary_constraint(a, b, c, mul, truediv, truediv)
A constant is a constraint as well, but one that is never sent any messages, because it involves only a single connector that it sets on construction.
>>> def constant(connector, value):
"""The constraint that connector = value."""
constraint = {}
connector['set_val'](constraint, value)
return constraint
These three constraints are sufficient to implement our temperature conversion network.
Representing connectors. A connector is represented as a dictionary that contains a value, but also has response functions with local state. The connector must track the informant that gave it its current value, and a list of constraints in which it participates.
The constructor connector has local functions for setting and forgetting values, which are the responses to messages from constraints.
>>> def connector(name=None):
"""A connector between constraints."""
informant = None
constraints = []
def set_value(source, value):
nonlocal informant
val = connector['val']
if val is None:
informant, connector['val'] = source, value
if name is not None:
print(name, '=', value)
inform_all_except(source, 'new_val', constraints)
else:
if val != value:
print('Contradiction detected:', val, 'vs', value)
def forget_value(source):
nonlocal informant
if informant == source:
informant, connector['val'] = None, None
if name is not None:
print(name, 'is forgotten')
inform_all_except(source, 'forget', constraints)
connector = {'val': None,
'set_val': set_value,
'forget': forget_value,
'has_val': lambda: connector['val'] is not None,
'connect': lambda source: constraints.append(source)}
return connector
A connector is again a dispatch dictionary for the five messages used by constraints to communicate with connectors. Four responses are functions, and the final response is the value itself.
The local function set_value is called when there is a request to set the connector's value. If the connector does not currently have a value, it will set its value and remember as informant the source constraint that requested the value to be set. Then the connector will notify all of its participating constraints except the constraint that requested the value to be set. This is accomplished using the following iterative function.
>>> def inform_all_except(source, message, constraints):
"""Inform all constraints of the message, except source."""
for c in constraints:
if c != source:
c[message]()
If a connector is asked to forget its value, it calls the local function forget-value, which first checks to make sure that the request is coming from the same constraint that set the value originally. If so, the connector informs its associated constraints about the loss of the value.
The response to the message has_val indicates whether the connector has a value. The response to the message connect adds the source constraint to the list of constraints.
The constraint program we have designed introduces many ideas that will appear again in object-oriented programming. Constraints and connectors are both abstractions that are manipulated through messages. When the value of a connector is changed, it is changed via a message that not only changes the value, but validates it (checking the source) and propagates its effects (informing other constraints). In fact, we will use a similar architecture of dictionaries with string-valued keys and functional values to implement an object-oriented system later in this chapter.
2.5 Object-Oriented Programming
Object-oriented programming (OOP) is a method for organizing programs that brings together many of the ideas introduced in this chapter. Like abstract data types, objects create an abstraction barrier between the use and implementation of data. Like dispatch dictionaries in message passing, objects respond to behavioral requests. Like mutable data structures, objects have local state that is not directly accessible from the global environment. The Python object system provides new syntax to promote the use of these techniques for organizing programs.
But the object system offers more than just convenience; it enables a new metaphor for designing programs in which several independent agents interact within the computer. Each object bundles together local state and behavior in a way that hides the complexity of both behind a data abstraction. Objects communicate with each other, and useful results are computed as a consequence of their interaction. Not only do objects pass messages, they also share behavior among other objects of the same type and inherit characteristics from related types.
The paradigm of object-oriented programming has its own vocabulary that reinforces the object metaphor. We have seen that an object is a data value that has methods and attributes, accessible via dot notation. Every object also has a type, called its class. To implement new types of data, we create new classes.
2.5.1 Objects and Classes
A class serves as a template for all objects whose type is that class. Every object is an instance of some particular class. The objects we have used so far all have built-in classes, but new classes can be defined similarly to how new functions can be defined. A class definition specifies the attributes and methods shared among objects of that class. We will introduce the class statement by revisiting the example of a bank account.
When introducing local state, we saw that bank accounts are naturally modeled as mutable values that have a balance. A bank account object should have a withdraw method that updates the account balance and returns the requested amount, if it is available. We would like additional behavior to complete the account abstraction: a bank account should be able to return its current balance, return the name of the account holder, and accept deposits.
An Account class allows us to create multiple instances of bank accounts. The act of creating a new object instance is known as instantiating the class. The syntax in Python for instantiating a class is identical to the syntax of calling a function. In this case, we call Account with the argument 'Jim', the account holder's name.
>>> a = Account('Jim')
An attribute of an object is a name-value pair associated with the object, which is accessible via dot notation. The attributes specific to a particular object, as opposed to all objects of a class, are called instance attributes. Each Account has its own balance and account holder name, which are examples of instance attributes. In the broader programming community, instance attributes may also be called fields, properties, or instance variables.
>>> a.holder 'Jim' >>> a.balance 0
Functions that operate on the object or perform object-specific computations are called methods. The side effects and return value of a method can depend upon, and change, other attributes of the object. For example, deposit is a method of our Account object a. It takes one argument, the amount to deposit, changes the balance attribute of the object, and returns the resulting balance.
>>> a.deposit(15) 15
In OOP, we say that methods are invoked on a particular object. As a result of invoking the withdraw method, either the withdrawal is approved and the amount is deducted and returned, or the request is declined and the account prints an error message.
>>> a.withdraw(10) # The withdraw method returns the balance after withdrawal 5 >>> a.balance # The balance attribute has changed 5 >>> a.withdraw(10) 'Insufficient funds'
As illustrated above, the behavior of a method can depend upon the changing attributes of the object. Two calls to withdraw with the same argument return different results.
2.5.2 Defining Classes
User-defined classes are created by class statements, which consist of a single clause. A class statement defines the class name and a base class (discussed in the section on Inheritance), then includes a suite of statements to define the attributes of the class:
class <name>(<base class>):
<suite>
When a class statement is executed, a new class is created and bound to <name> in the first frame of the current environment. The suite is then executed. Any names bound within the <suite> of a class statement, through def or assignment statements, create or modify attributes of the class.
Classes are typically organized around manipulating instance attributes, which are the name-value pairs associated not with the class itself, but with each object of that class. The class specifies the instance attributes of its objects by defining a method for initializing new objects. For instance, part of initializing an object of the Account class is to assign it a starting balance of 0.
The <suite> of a class statement contains def statements that define new methods for objects of that class. The method that initializes objects has a special name in Python, __init__ (two underscores on each side of "init"), and is called the constructor for the class.
>>> class Account(object):
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
The __init__ method for Account has two formal parameters. The first one, self, is bound to the newly created Account object. The second parameter, account_holder, is bound to the argument passed to the class when it is called to be instantiated.
The constructor binds the instance attribute name balance to 0. It also binds the attribute name holder to the value of the name account_holder. The formal parameter account_holder is a local name to the __init__ method. On the other hand, the name holder that is bound via the final assignment statement persists, because it is stored as an attribute of self using dot notation.
Having defined the Account class, we can instantiate it.
>>> a = Account('Jim')
This "call" to the Account class creates a new object that is an instance of Account, then calls the constructor function __init__ with two arguments: the newly created object and the string 'Jim'. By convention, we use the parameter name self for the first argument of a constructor, because it is bound to the object being instantiated. This convention is adopted in virtually all Python code.
Now, we can access the object's balance and holder using dot notation.
>>> a.balance 0 >>> a.holder 'Jim'
Identity. Each new account instance has its own balance attribute, the value of which is independent of other objects of the same class.
>>> b = Account('Jack')
>>> b.balance = 200
>>> [acc.balance for acc in (a, b)]
[0, 200]
To enforce this separation, every object that is an instance of a user-defined class has a unique identity. Object identity is compared using the is and is not operators.
>>> a is a True >>> a is not b True
Despite being constructed from identical calls, the objects bound to a and b are not the same. As usual, binding an object to a new name using assignment does not create a new object.
>>> c = a >>> c is a True
New objects that have user-defined classes are only created when a class (such as Account) is instantiated with call expression syntax.
Methods. Object methods are also defined by a def statement in the suite of a class statement. Below, deposit and withdraw are both defined as methods on objects of the Account class.
>>> class Account(object):
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
def deposit(self, amount):
self.balance = self.balance + amount
return self.balance
def withdraw(self, amount):
if amount > self.balance:
return 'Insufficient funds'
self.balance = self.balance - amount
return self.balance
While method definitions do not differ from function definitions in how they are declared, method definitions do have a different effect. The function value that is created by a def statement within a class statement is bound to the declared name, but bound locally within the class as an attribute. That value is invoked as a method using dot notation from an instance of the class.
Each method definition again includes a special first parameter self, which is bound to the object on which the method is invoked. For example, let us say that deposit is invoked on a particular Account object and passed a single argument value: the amount deposited. The object itself is bound to self, while the argument is bound to amount. All invoked methods have access to the object via the self parameter, and so they can all access and manipulate the object's state.
To invoke these methods, we again use dot notation, as illustrated below.
>>> tom_account = Account('Tom')
>>> tom_account.deposit(100)
100
>>> tom_account.withdraw(90)
10
>>> tom_account.withdraw(90)
'Insufficient funds'
>>> tom_account.holder
'Tom'
When a method is invoked via dot notation, the object itself (bound to tom_account, in this case) plays a dual role. First, it determines what the name withdraw means; withdraw is not a name in the environment, but instead a name that is local to the Account class. Second, it is bound to the first parameter self when the withdraw method is invoked. The details of the procedure for evaluating dot notation follow in the next section.
2.5.3 Message Passing and Dot Expressions
Methods, which are defined in classes, and instance attributes, which are typically assigned in constructors, are the fundamental elements of object-oriented programming. These two concepts replicate much of the behavior of a dispatch dictionary in a message passing implementation of a data value. Objects take messages using dot notation, but instead of those messages being arbitrary string-valued keys, they are names local to a class. Objects also have named local state values (the instance attributes), but that state can be accessed and manipulated using dot notation, without having to employ nonlocal statements in the implementation.
The central idea in message passing was that data values should have behavior by responding to messages that are relevant to the abstract type they represent. Dot notation is a syntactic feature of Python that formalizes the message passing metaphor. The advantage of using a language with a built-in object system is that message passing can interact seamlessly with other language features, such as assignment statements. We do not require different messages to "get" or "set" the value associated with a local attribute name; the language syntax allows us to use the message name directly.
Dot expressions. The code fragment tom_account.deposit is called a dot expression. A dot expression consists of an expression, a dot, and a name:
<expression> . <name>
The <expression> can be any valid Python expression, but the <name> must be a simple name (not an expression that evaluates to a name). A dot expression evaluates to the value of the attribute with the given <name>, for the object that is the value of the <expression>.
The built-in function getattr also returns an attribute for an object by name. It is the function equivalent of dot notation. Using getattr, we can look up an attribute using a string, just as we did with a dispatch dictionary.
>>> getattr(tom_account, 'balance') 10
We can also test whether an object has a named attribute with hasattr.
>>> hasattr(tom_account, 'deposit') True
The attributes of an object include all of its instance attributes, along with all of the attributes (including methods) defined in its class. Methods are attributes of the class that require special handling.
Method and functions. When a method is invoked on an object, that object is implicitly passed as the first argument to the method. That is, the object that is the value of the <expression> to the left of the dot is passed automatically as the first argument to the method named on the right side of the dot expression. As a result, the object is bound to the parameter self.
To achieve automatic self binding, Python distinguishes between functions, which we have been creating since the beginning of the text, and bound methods, which couple together a function and the object on which that method will be invoked. A bound method value is already associated with its first argument, the instance on which it was invoked, which will be named self when the method is called.
We can see the difference in the interactive interpreter by calling type on the returned values of dot expressions. As an attribute of a class, a method is just a function, but as an attribute of an instance, it is a bound method:
>>> type(Account.deposit) <class 'function'> >>> type(tom_account.deposit) <class 'method'>
These two results differ only in the fact that the first is a standard two-argument function with parameters self and amount. The second is a one-argument method, where the name self will be bound to the object named tom_account automatically when the method is called, while the parameter amount will be bound to the argument passed to the method. Both of these values, whether function values or bound method values, are associated with the same deposit function body.
We can call deposit in two ways: as a function and as a bound method. In the former case, we must supply an argument for the self parameter explicitly. In the latter case, the self parameter is bound automatically.
>>> Account.deposit(tom_account, 1001) # The deposit function requires 2 arguments 1011 >>> tom_account.deposit(1000) # The deposit method takes 1 argument 2011
The function getattr behaves exactly like dot notation: if its first argument is an object but the name is a method defined in the class, then getattr returns a bound method value. On the other hand, if the first argument is a class, then getattr returns the attribute value directly, which is a plain function.
Practical guidance: naming conventions. Class names are conventionally written using the CapWords convention (also called CamelCase because the capital letters in the middle of a name are like humps). Method names follow the standard convention of naming functions using lowercased words separated by underscores.
In some cases, there are instance variables and methods that are related to the maintenance and consistency of an object that we don't want users of the object to see or use. They are not part of the abstraction defined by a class, but instead part of the implementation. Python's convention dictates that if an attribute name starts with an underscore, it should only be accessed within methods of the class itself, rather than by users of the class.
2.5.4 Class Attributes
Some attribute values are shared across all objects of a given class. Such attributes are associated with the class itself, rather than any individual instance of the class. For instance, let us say that a bank pays interest on the balance of accounts at a fixed interest rate. That interest rate may change, but it is a single value shared across all accounts.
Class attributes are created by assignment statements in the suite of a class statement, outside of any method definition. In the broader developer community, class attributes may also be called class variables or static variables. The following class statement creates a class attribute for Account with the name interest.
>>> class Account(object):
interest = 0.02 # A class attribute
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
# Additional methods would be defined here
This attribute can still be accessed from any instance of the class.
>>> tom_account = Account('Tom')
>>> jim_account = Account('Jim')
>>> tom_account.interest
0.02
>>> jim_account.interest
0.02
However, a single assignment statement to a class attribute changes the value of the attribute for all instances of the class.
>>> Account.interest = 0.04 >>> tom_account.interest 0.04 >>> jim_account.interest 0.04
Attribute names. We have introduced enough complexity into our object system that we have to specify how names are resolved to particular attributes. After all, we could easily have a class attribute and an instance attribute with the same name.
As we have seen, a dot expressions consist of an expression, a dot, and a name:
<expression> . <name>
To evaluate a dot expression:
- Evaluate the <expression> to the left of the dot, which yields the object of the dot expression.
- <name> is matched against the instance attributes of that object; if an attribute with that name exists, its value is returned.
- If <name> does not appear among instance attributes, then <name> is looked up in the class, which yields a class attribute value.
- That value is returned unless it is a function, in which case a bound method is returned instead.
In this evaluation procedure, instance attributes are found before class attributes, just as local names have priority over global in an environment. Methods defined within the class are bound to the object of the dot expression during the third step of this evaluation procedure. The procedure for looking up a name in a class has additional nuances that will arise shortly, once we introduce class inheritance.
Assignment. All assignment statements that contain a dot expression on their left-hand side affect attributes for the object of that dot expression. If the object is an instance, then assignment sets an instance attribute. If the object is a class, then assignment sets a class attribute. As a consequence of this rule, assignment to an attribute of an object cannot affect the attributes of its class. The examples below illustrate this distinction.
If we assign to the named attribute interest of an account instance, we create a new instance attribute that has the same name as the existing class attribute.
>>> jim_account.interest = 0.08
and that attribute value will be returned from a dot expression.
>>> jim_account.interest 0.08
However, the class attribute interest still retains its original value, which is returned for all other accounts.
>>> tom_account.interest 0.04
Changes to the class attribute interest will affect tom_account, but the instance attribute for jim_account will be unaffected.
>>> Account.interest = 0.05 # changing the class attribute >>> tom_account.interest # changes instances without like-named instance attributes 0.05 >>> jim_account.interest # but the existing instance attribute is unaffected 0.08
2.5.5 Inheritance
When working in the OOP paradigm, we often find that different abstract data types are related. In particular, we find that similar classes differ in their amount of specialization. Two classes may have similar attributes, but one represents a special case of the other.
For example, we may want to implement a checking account, which is different from a standard account. A checking account charges an extra $1 for each withdrawal and has a lower interest rate. Here, we demonstrate the desired behavior.
>>> ch = CheckingAccount('Tom')
>>> ch.interest # Lower interest rate for checking accounts
0.01
>>> ch.deposit(20) # Deposits are the same
20
>>> ch.withdraw(5) # withdrawals decrease balance by an extra charge
14
A CheckingAccount is a specialization of an Account. In OOP terminology, the generic account will serve as the base class of CheckingAccount, while CheckingAccount will be a subclass of Account. (The terms parent class and superclass are also used for the base class, while child class is also used for the subclass.)
A subclass inherits the attributes of its base class, but may override certain attributes, including certain methods. With inheritance, we only specify what is different between the subclass and the base class. Anything that we leave unspecified in the subclass is automatically assumed to behave just as it would for the base class.
Inheritance also has a role in our object metaphor, in addition to being a useful organizational feature. Inheritance is meant to represent is-a relationships between classes, which contrast with has-a relationships. A checking account is-a specific type of account, so having a CheckingAccount inherit from Account is an appropriate use of inheritance. On the other hand, a bank has-a list of bank accounts that it manages, so neither should inherit from the other. Instead, a list of account objects would be naturally expressed as an instance attribute of a bank object.
2.5.6 Using Inheritance
We specify inheritance by putting the base class in parentheses after the class name. First, we give a full implementation of the Account class, which includes docstrings for the class and its methods.
>>> class Account(object):
"""A bank account that has a non-negative balance."""
interest = 0.02
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
def deposit(self, amount):
"""Increase the account balance by amount and return the new balance."""
self.balance = self.balance + amount
return self.balance
def withdraw(self, amount):
"""Decrease the account balance by amount and return the new balance."""
if amount > self.balance:
return 'Insufficient funds'
self.balance = self.balance - amount
return self.balance
A full implementation of CheckingAccount appears below.
>>> class CheckingAccount(Account):
"""A bank account that charges for withdrawals."""
withdraw_charge = 1
interest = 0.01
def withdraw(self, amount):
return Account.withdraw(self, amount + self.withdraw_charge)
Here, we introduce a class attribute withdraw_charge that is specific to the CheckingAccount class. We assign a lower value to the interest attribute. We also define a new withdraw method to override the behavior defined in the Account class. With no further statements in the class suite, all other behavior is inherited from the base class Account.
>>> checking = CheckingAccount('Sam')
>>> checking.deposit(10)
10
>>> checking.withdraw(5)
4
>>> checking.interest
0.01
The expression checking.deposit evaluates to a bound method for making deposits, which was defined in the Account class. When Python resolves a name in a dot expression that is not an attribute of the instance, it looks up the name in the class. In fact, the act of "looking up" a name in a class tries to find that name in every base class in the inheritance chain for the original object's class. We can define this procedure recursively. To look up a name in a class.
- If it names an attribute in the class, return the attribute value.
- Otherwise, look up the name in the base class, if there is one.
In the case of deposit, Python would have looked for the name first on the instance, and then in the CheckingAccount class. Finally, it would look in the Account class, where deposit is defined. According to our evaluation rule for dot expressions, since deposit is a function looked up in the class for the checking instance, the dot expression evaluates to a bound method value. That method is invoked with the argument 10, which calls the deposit method with self bound to the checking object and amount bound to 10.
The class of an object stays constant throughout. Even though the deposit method was found in the Account class, deposit is called with self bound to an instance of CheckingAccount, not of Account.
Calling ancestors. Attributes that have been overridden are still accessible via class objects. For instance, we implemented the withdraw method of CheckingAccount by calling the withdraw method of Account with an argument that included the withdraw_charge.
Notice that we called self.withdraw_charge rather than the equivalent CheckingAccount.withdraw_charge. The benefit of the former over the latter is that a class that inherits from CheckingAccount might override the withdrawal charge. If that is the case, we would like our implementation of withdraw to find that new value instead of the old one.
Object Abstractions. It is extremely common in object-oriented programs that different types of objects will share the same attribute names. An object abstraction is a collection of attributes and conditions on those attributes. For example, all accounts must have deposit and withdraw methods that take numerical arguments, as well as a balance attribute. The classes Account and CheckingAccount both implement this abstraction. Inheritance specifically promotes name sharing in this way.
The parts of your program that use objects (rather than implementing them) are most robust to future changes if they do not make assumptions about object types, but instead only about their attribute names. That is, they use the object abstraction, rather than assuming anything about its implementation. For example, let us say that we run a lottery, and we wish to deposit $5 into each of a list of accounts. The following implementation does not assume anything about the types of those accounts, and therefore works equally well with any type of object that has a deposit method:
>>> def deposit_all(winners, amount=5):
for account in winners:
account.deposit(amount)
The function deposit_all above assumes only that each account satisfies the account object abstraction, and so it will work with any other account classes that also implement this abstraction. Assuming a particular class of account would violate the abstraction barrier of the account object abstraction. For example, the following implementation will not necessarily work with new kinds of accounts:
>>> def deposit_all(winners, amount=5):
for account in winners:
Account.deposit(account, amount)
2.5.7 Multiple Inheritance
Python supports the concept of a subclass inheriting attributes from multiple base classes, a language feature called multiple inheritance.
Suppose that we have a SavingsAccount that inherits from Account, but charges customers a small fee every time they make a deposit.
>>> class SavingsAccount(Account):
deposit_charge = 2
def deposit(self, amount):
return Account.deposit(self, amount - self.deposit_charge)
Then, a clever executive conceives of an AsSeenOnTVAccount account with the best features of both CheckingAccount and SavingsAccount: withdrawal fees, deposit fees, and a low interest rate. It's both a checking and a savings account in one! "If we build it," the executive reasons, "someone will sign up and pay all those fees. We'll even give them a dollar."
>>> class AsSeenOnTVAccount(CheckingAccount, SavingsAccount):
def __init__(self, account_holder):
self.holder = account_holder
self.balance = 1 # A free dollar!
In fact, this implementation is complete. Both withdrawal and deposits will generate fees, using the function definitions in CheckingAccount and SavingsAccount respectively.
>>> such_a_deal = AsSeenOnTVAccount("John")
>>> such_a_deal.balance
1
>>> such_a_deal.deposit(20) # $2 fee from SavingsAccount.deposit
19
>>> such_a_deal.withdraw(5) # $1 fee from CheckingAccount.withdraw
13
Non-ambiguous references are resolved correctly as expected:
>>> such_a_deal.deposit_charge 2 >>> such_a_deal.withdraw_charge 1
But what about when the reference is ambiguous, such as the reference to the withdraw method that is defined in both Account and CheckingAccount? The figure below depicts an inheritance graph for the AsSeenOnTVAccount class. Each arrow points from a subclass to a base class.
For a simple "diamond" shape like this, Python resolves names from left to right, then upwards. In this example, Python checks for an attribute name in the following classes, in order, until an attribute with that name is found:
AsSeenOnTVAccount, CheckingAccount, SavingsAccount, Account, object
There is no correct solution to the inheritance ordering problem, as there are cases in which we might prefer to give precedence to certain inherited classes over others. However, any programming language that supports multiple inheritance must select some ordering in a consistent way, so that users of the language can predict the behavior of their programs.
Further reading. Python resolves this name using a recursive algorithm called the C3 Method Resolution Ordering. The method resolution order of any class can be queried using the mro method on all classes.
>>> [c.__name__ for c in AsSeenOnTVAccount.mro()] ['AsSeenOnTVAccount', 'CheckingAccount', 'SavingsAccount', 'Account', 'object']
The precise algorithm for finding method resolution orderings is not a topic for this text, but is described by Python's primary author with a reference to the original paper.
2.5.8 Functions as Objects
In some languages, such as Python and Ruby, functions themselves are objects, i.e. instances of special classes. For example, functions built into the interpreter are instances of the builtin_function_or_method class:
>>> type(pow) <class 'builtin_function_or_method'>
Similarly, as demonstrated above for the deposit function and method, user-defined functions are instances of function, and user-defined methods are instances of method:
>>> type(Account.deposit) <class 'function'> >>> type(tom_account.deposit) <class 'method'>
By calling mro on the resulting types, we can see that they all inherit from object, just like the classes we defined above. (The names builtin_function_or_method, function, and method are not bound in the global namespace, so we cannot directly call mro on them.)
>>> [c.__name__ for c in type(pow).mro()] ['builtin_function_or_method', 'object'] >>> [c.__name__ for c in type(Account.deposit).mro()] ['function', 'object'] >>> [c.__name__ for c in type(tom_account.deposit).mro()] ['method', 'object']
Since functions are objects, they have attributes just like any other object. For example, all functions have a __name__ attribute:
>>> pow.__name__ 'pow'
Attributes can also be added to user-defined functions, and most existing attributes can be modified. Methods and built-in functions, however, don't allow adding or changing attributes.
>>> def my_pow(x, y):
return pow(x, y)
>>> my_pow <function my_pow at 0x7f77b2558270> >>> my_pow.__name__ = "power" # change attribute >>> my_pow <function power at 0x7f77b2558270> >>> my_pow.value = 42 # new attribute >>> my_pow.value 42
(Note: As of Python 3.3, functions have a __qualname__ attribute that is used in many places instead of __name__. In the example above, it is the __qualname__ attribute that must be changed instead of __name__ to achieve the same behavior in Python 3.3.)
Function attributes allow us to store function-specific data with the function itself, without polluting the global namespace.
2.5.9 The Role of Objects
The Python object system is designed to make data abstraction and message passing both convenient and flexible. The specialized syntax of classes, methods, inheritance, and dot expressions all enable us to formalize the object metaphor in our programs, which improves our ability to organize large programs.
In particular, we would like our object system to promote a separation of concerns among the different aspects of the program. Each object in a program encapsulates and manages some part of the program's state, and each class statement defines the functions that implement some part of the program's overall logic. Abstraction barriers enforce the boundaries between different aspects of a large program.
Object-oriented programming is particularly well-suited to programs that model systems that have separate but interacting parts. For instance, different users interact in a social network, different characters interact in a game, and different shapes interact in a physical simulation. When representing such systems, the objects in a program often map naturally onto objects in the system being modeled, and classes represent their types and relationships.
On the other hand, classes may not provide the best mechanism for implementing certain abstractions. Functional abstractions provide a more natural metaphor for representing relationships between inputs and outputs. One should not feel compelled to fit every bit of logic in a program within a class, especially when defining independent functions for manipulating data is more natural. Functions can also enforce a separation of concerns.
Multi-paradigm languages like Python allow programmers to match organizational paradigms to appropriate problems. Learning to identify when to introduce a new class, as opposed to a new function, in order to simplify or modularize a program, is an important design skill in software engineering that deserves careful attention.
2.6 Bonus Material: Implementing Classes and Objects
When working in the object-oriented programming paradigm, we use the object metaphor to guide the organization of our programs. Most logic about how to represent and manipulate data is expressed within class declarations. In this section, we see that classes and objects can themselves be represented using just functions and dictionaries. The purpose of implementing an object system in this way is to illustrate that using the object metaphor does not require a special programming language. Programs can be object-oriented, even in programming languages that do not have a built-in object system.
In order to implement objects, we will abandon dot notation (which does require built-in language support), but create dispatch dictionaries that behave in much the same way as the elements of the built-in object system. We have already seen how to implement message-passing behavior through dispatch dictionaries. To implement an object system in full, we send messages between instances, classes, and base classes, all of which are dictionaries that contain attributes.
We will not implement the entire Python object system, which includes features that we have not covered in this text (e.g., meta-classes and static methods). We will focus instead on user-defined classes without multiple inheritance and without introspective behavior (such as returning the class of an instance). Our implementation is not meant to follow the precise specification of the Python type system. Instead, it is designed to implement the core functionality that enables the object metaphor.
2.6.1 Instances
We begin with instances. An instance has named attributes, such as the balance of an account, which can be set and retrieved. We implement an instance using a dispatch dictionary that responds to messages that "get" and "set" attribute values. Attributes themselves are stored in a local dictionary called attributes.
As we have seen previously in this chapter, dictionaries themselves are abstract data types. We implemented dictionaries with lists, we implemented lists with pairs, and we implemented pairs with functions. As we implement an object system in terms of dictionaries, keep in mind that we could just as well be implementing objects using functions alone.
To begin our implementation, we assume that we have a class implementation that can look up any names that are not part of the instance. We pass in a class to make_instance as the parameter cls.
>>> def make_instance(cls):
"""Return a new object instance, which is a dispatch dictionary."""
def get_value(name):
if name in attributes:
return attributes[name]
else:
value = cls['get'](name)
return bind_method(value, instance)
def set_value(name, value):
attributes[name] = value
attributes = {}
instance = {'get': get_value, 'set': set_value}
return instance
The instance is a dispatch dictionary that responds to the messages get and set. The set message corresponds to attribute assignment in Python's object system: all assigned attributes are stored directly within the object's local attribute dictionary. In get, if name does not appear in the local attributes dictionary, then it is looked up in the class. If the value returned by cls is a function, it must be bound to the instance.
Bound method values. The get_value function in make_instance finds a named attribute in its class with get, then calls bind_method. Binding a method only applies to function values, and it creates a bound method value from a function value by inserting the instance as the first argument:
>>> def bind_method(value, instance):
"""Return a bound method if value is callable, or value otherwise."""
if callable(value):
def method(*args):
return value(instance, *args)
return method
else:
return value
When a method is called, the first parameter self will be bound to the value of instance by this definition.
2.6.2 Classes
A class is also an object, both in Python's object system and the system we are implementing here. For simplicity, we say that classes do not themselves have a class. (In Python, classes do have classes; almost all classes share the same class, called type.) A class can respond to get and set messages, as well as the new message:
>>> def make_class(attributes, base_class=None):
"""Return a new class, which is a dispatch dictionary."""
def get_value(name):
if name in attributes:
return attributes[name]
elif base_class is not None:
return base_class['get'](name)
def set_value(name, value):
attributes[name] = value
def new(*args):
return init_instance(cls, *args)
cls = {'get': get_value, 'set': set_value, 'new': new}
return cls
Unlike an instance, the get function for classes does not query its class when an attribute is not found, but instead queries its base_class. No method binding is required for classes.
Initialization. The new function in make_class calls init_instance, which first makes a new instance, then invokes a method called __init__.
>>> def init_instance(cls, *args):
"""Return a new object with type cls, initialized with args."""
instance = make_instance(cls)
init = cls['get']('__init__')
if init:
init(instance, *args)
return instance
This final function completes our object system. We now have instances, which set locally but fall back to their classes on get. After an instance looks up a name in its class, it binds itself to function values to create methods. Finally, classes can create new instances, and they apply their __init__ constructor function immediately after instance creation.
In this object system, the only function that should be called by the user is make_class. All other functionality is enabled through message passing. Similarly, Python's object system is invoked via the class statement, and all of its other functionality is enabled through dot expressions and calls to classes.
2.6.3 Using Implemented Objects
We now return to use the bank account example from the previous section. Using our implemented object system, we will create an Account class, a CheckingAccount subclass, and an instance of each.
The Account class is created through a make_account_class function, which has structure similar to a class statement in Python, but concludes with a call to make_class.
>>> def make_account_class():
"""Return the Account class, which has deposit and withdraw methods."""
def __init__(self, account_holder):
self['set']('holder', account_holder)
self['set']('balance', 0)
def deposit(self, amount):
"""Increase the account balance by amount and return the new balance."""
new_balance = self['get']('balance') + amount
self['set']('balance', new_balance)
return self['get']('balance')
def withdraw(self, amount):
"""Decrease the account balance by amount and return the new balance."""
balance = self['get']('balance')
if amount > balance:
return 'Insufficient funds'
self['set']('balance', balance - amount)
return self['get']('balance')
return make_class(locals())
The final call to locals returns a dictionary with string keys that contains the name-value bindings in the current local frame.
The Account class is finally instantiated via assignment.
>>> Account = make_account_class()
Then, an account instance is created via the new message, which requires a name to go with the newly created account.
>>> jim_acct = Account['new']('Jim')
Then, get messages passed to jim_acct retrieve properties and methods. Methods can be called to update the balance of the account.
>>> jim_acct['get']('holder')
'Jim'
>>> jim_acct['get']('interest')
0.02
>>> jim_acct['get']('deposit')(20)
20
>>> jim_acct['get']('withdraw')(5)
15
As with the Python object system, setting an attribute of an instance does not change the corresponding attribute of its class.
>>> jim_acct['set']('interest', 0.04)
>>> Account['get']('interest')
0.02
Inheritance. We can create a subclass CheckingAccount by overloading a subset of the class attributes. In this case, we change the withdraw method to impose a fee, and we reduce the interest rate.
>>> def make_checking_account_class():
"""Return the CheckingAccount class, which imposes a $1 withdrawal fee."""
interest = 0.01
withdraw_fee = 1
def withdraw(self, amount):
fee = self['get']('withdraw_fee')
return Account['get']('withdraw')(self, amount + fee)
return make_class(locals(), Account)
In this implementation, we call the withdraw function of the base class Account from the withdraw function of the subclass, as we would in Python's built-in object system. We can create the subclass itself and an instance, as before.
>>> CheckingAccount = make_checking_account_class()
>>> jack_acct = CheckingAccount['new']('Jack')
Deposits behave identically, as does the constructor function. withdrawals impose the $1 fee from the specialized withdraw method, and interest has the new lower value from CheckingAccount.
>>> jack_acct['get']('interest')
0.01
>>> jack_acct['get']('deposit')(20)
20
>>> jack_acct['get']('withdraw')(5)
14
Our object system built upon dictionaries is quite similar in implementation to the built-in object system in Python. In Python, an instance of any user-defined class has a special attribute __dict__ that stores the local instance attributes for that object in a dictionary, much like our attributes dictionary. Python differs because it distinguishes certain special methods that interact with built-in functions to ensure that those functions behave correctly for arguments of many different types. Functions that operate on different types are the subject of the next section.
2.7 Generic Operations
In this chapter, we introduced compound data values, along with the technique of data abstraction using constructors and selectors. Using message passing, we endowed our abstract data types with behavior directly. Using the object metaphor, we bundled together the representation of data and the methods used to manipulate that data to modularize data-driven programs with local state.
However, we have yet to show that our object system allows us to combine together different types of objects flexibly in a large program. Message passing via dot expressions is only one way of building combined expressions with multiple objects. In this section, we explore alternate methods for combining and manipulating objects of different types.
2.7.1 String Conversion
We stated in the beginning of this chapter that an object value should behave like the kind of data it is meant to represent, including producing a string representation of itself. String representations of data values are especially important in an interactive language like Python, where the read-eval-print loop requires every value to have some sort of string representation.
String values provide a fundamental medium for communicating information among humans. Sequences of characters can be rendered on a screen, printed to paper, read aloud, converted to braille, or broadcast as Morse code. Strings are also fundamental to programming because they can represent Python expressions. For an object, we may want to generate a string that, when interpreted as a Python expression, evaluates to an equivalent object.
Python stipulates that all objects should produce two different string representations: one that is human-interpretable text and one that is a Python-interpretable expression. The constructor function for strings, str, returns a human-readable string. Where possible, the repr function returns a Python expression that evaluates to an equal object. The docstring for repr explains this property:
repr(object) -> string Return the canonical string representation of the object. For most object types, eval(repr(object)) == object.
The result of calling repr on the value of an expression is what Python prints in an interactive session.
>>> 12e12 12000000000000.0 >>> print(repr(12e12)) 12000000000000.0
In cases where no representation exists that evaluates to the original value, Python produces a proxy.
>>> repr(min) '<built-in function min>'
The str constructor often coincides with repr, but provides a more interpretable text representation in some cases. For instance, we see a difference between str and repr with dates.
>>> from datetime import date >>> today = date(2011, 9, 12) >>> repr(today) 'datetime.date(2011, 9, 12)' >>> str(today) '2011-09-12'
Defining the repr function presents a new challenge: we would like it to apply correctly to all data types, even those that did not exist when repr was implemented. We would like it to be a polymorphic function, one that can be applied to many (poly) different forms (morph) of data.
Message passing provides an elegant solution in this case: the repr function invokes a method called __repr__ on its argument.
>>> today.__repr__() 'datetime.date(2011, 9, 12)'
By implementing this same method in user-defined classes, we can extend the applicability of repr to any class we create in the future. This example highlights another benefit of message passing in general, that it provides a mechanism for extending the domain of existing functions to new object types.
The str constructor is implemented in a similar manner: it invokes a method called __str__ on its argument.
>>> today.__str__() '2011-09-12'
These polymorphic functions are examples of a more general principle: certain functions should apply to multiple data types. The message passing approach exemplified here is only one of a family of techniques for implementing polymorphic functions. The remainder of this section explores some alternatives.
2.7.2 Multiple Representations
Data abstraction, using objects or functions, is a powerful tool for managing complexity. Abstract data types allow us to construct an abstraction barrier between the underlying representation of data and the functions or messages used to manipulate it. However, in large programs, it may not always make sense to speak of "the underlying representation" for a data type in a program. For one thing, there might be more than one useful representation for a data object, and we might like to design systems that can deal with multiple representations.
To take a simple example, complex numbers may be represented in two almost equivalent ways: in rectangular form (real and imaginary parts) and in polar form (magnitude and angle). Sometimes the rectangular form is more appropriate and sometimes the polar form is more appropriate. Indeed, it is perfectly plausible to imagine a system in which complex numbers are represented in both ways, and in which the functions for manipulating complex numbers work with either representation.
More importantly, large software systems are often designed by many people working over extended periods of time, subject to requirements that change over time. In such an environment, it is simply not possible for everyone to agree in advance on choices of data representation. In addition to the data-abstraction barriers that isolate representation from use, we need abstraction barriers that isolate different design choices from each other and permit different choices to coexist in a single program. Furthermore, since large programs are often created by combining pre-existing modules that were designed in isolation, we need conventions that permit programmers to incorporate modules into larger systems additively, that is, without having to redesign or re-implement these modules.
We begin with the simple complex-number example. We will see how message passing enables us to design separate rectangular and polar representations for complex numbers while maintaining the notion of an abstract "complex-number" object. We will accomplish this by defining arithmetic functions for complex numbers (add_complex, mul_complex) in terms of generic selectors that access parts of a complex number independent of how the number is represented. The resulting complex-number system contains two different kinds of abstraction barriers. They isolate higher-level operations from lower-level representations. In addition, there is a vertical barrier that gives us the ability to separately design alternative representations.

As a side note, we are developing a system that performs arithmetic operations on complex numbers as a simple but unrealistic example of a program that uses generic operations. A complex number type is actually built into Python, but for this example we will implement our own.
Like rational numbers, complex numbers are naturally represented as pairs. The set of complex numbers can be thought of as a two-dimensional space with two orthogonal axes, the real axis and the imaginary axis. From this point of view, the complex number z = x + y * i (where i*i = -1) can be thought of as the point in the plane whose real coordinate is x and whose imaginary coordinate is y. Adding complex numbers involves adding their respective x and y coordinates.
When multiplying complex numbers, it is more natural to think in terms of representing a complex number in polar form, as a magnitude and an angle. The product of two complex numbers is the vector obtained by stretching one complex number by a factor of the length of the other, and then rotating it through the angle of the other.
Thus, there are two different representations for complex numbers, which are appropriate for different operations. Yet, from the viewpoint of someone writing a program that uses complex numbers, the principle of data abstraction suggests that all the operations for manipulating complex numbers should be available regardless of which representation is used by the computer.
Interfaces. Message passing not only provides a method for coupling behavior and data, it allows different data types to respond to the same message in different ways. A shared message that elicits similar behavior from different object classes is a powerful method of abstraction.
As we have seen, an abstract data type is defined by constructors, selectors, and additional behavior conditions. A closely related concept is an interface, which is a set of shared messages, along with a specification of what they mean. Objects that respond to the special __repr__ and __str__ methods all implement a common interface of types that can be represented as strings.
In the case of complex numbers, the interface needed to implement arithmetic consists of four messages: real, imag, magnitude, and angle. We can implement addition and multiplication in terms of these messages.
We can have two different abstract data types for complex numbers that differ in their constructors.
- ComplexRI constructs a complex number from real and imaginary parts.
- ComplexMA constructs a complex number from a magnitude and angle.
With these messages and constructors, we can implement complex arithmetic.
>>> def add_complex(z1, z2):
return ComplexRI(z1.real + z2.real, z1.imag + z2.imag)
>>> def mul_complex(z1, z2):
return ComplexMA(z1.magnitude * z2.magnitude, z1.angle + z2.angle)
The relationship between the terms "abstract data type" (ADT) and "interface" is subtle. An ADT includes ways of building complex data types, manipulating them as units, and selecting for their components. In an object-oriented system, an ADT corresponds to a class, although we have seen that an object system is not needed to implement an ADT. An interface is a set of messages that have associated meanings, and which may or may not include selectors. Conceptually, an ADT describes a full representational abstraction of some kind of thing, whereas an interface specifies a set of behaviors that may be shared across many things.
Properties. We would like to use both types of complex numbers interchangeably, but it would be wasteful to store redundant information about each number. We would like to store either the real-imaginary representation or the magnitude-angle representation.
Python has a simple feature for computing attributes on the fly from zero-argument functions. The @property decorator allows functions to be called without the standard call expression syntax. An implementation of complex numbers in terms of real and imaginary parts illustrates this point.
>>> from math import atan2
>>> class ComplexRI(object):
def __init__(self, real, imag):
self.real = real
self.imag = imag
@property
def magnitude(self):
return (self.real ** 2 + self.imag ** 2) ** 0.5
@property
def angle(self):
return atan2(self.imag, self.real)
def __repr__(self):
return 'ComplexRI({0}, {1})'.format(self.real, self.imag)
A second implementation using magnitude and angle provides the same interface because it responds to the same set of messages.
>>> from math import sin, cos
>>> class ComplexMA(object):
def __init__(self, magnitude, angle):
self.magnitude = magnitude
self.angle = angle
@property
def real(self):
return self.magnitude * cos(self.angle)
@property
def imag(self):
return self.magnitude * sin(self.angle)
def __repr__(self):
return 'ComplexMA({0}, {1})'.format(self.magnitude, self.angle)
In fact, our implementations of add_complex and mul_complex are now complete; either class of complex number can be used for either argument in either complex arithmetic function. It is worth noting that the object system does not explicitly connect the two complex types in any way (e.g., through inheritance). We have implemented the complex number abstraction by sharing a common set of messages, an interface, across the two classes.
>>> from math import pi >>> add_complex(ComplexRI(1, 2), ComplexMA(2, pi/2)) ComplexRI(1.0000000000000002, 4.0) >>> mul_complex(ComplexRI(0, 1), ComplexRI(0, 1)) ComplexMA(1.0, 3.141592653589793)
The interface approach to encoding multiple representations has appealing properties. The class for each representation can be developed separately; they must only agree on the names of the attributes they share. The interface is also additive. If another programmer wanted to add a third representation of complex numbers to the same program, they would only have to create another class with the same attributes.
2.7.3 Special Methods
The built-in mathematical operators can be extended in much the same way as repr; there are special method names corresponding to Python operators for arithmetic, logical, and sequence operations.
To make our code more legible, we would perhaps like to use the + and * operators directly when adding and multiplying complex numbers. Adding the following methods to both of our complex number classes will enable these operators to be used, as well as the add and mul functions in the operator module:
>>> ComplexRI.__add__ = lambda self, other: add_complex(self, other) >>> ComplexMA.__add__ = lambda self, other: add_complex(self, other) >>> ComplexRI.__mul__ = lambda self, other: mul_complex(self, other) >>> ComplexMA.__mul__ = lambda self, other: mul_complex(self, other)
Now, we can use infix notation with our user-defined classes.
>>> ComplexRI(1, 2) + ComplexMA(2, 0) ComplexRI(3.0, 2.0) >>> ComplexRI(0, 1) * ComplexRI(0, 1) ComplexMA(1.0, 3.141592653589793)
True and false values. We saw previously that numbers in Python have a truth value; more specifically, 0 is a false value and all other numbers are true values. In fact, all objects in Python have a truth value. By default, objects are considered to be true, but the special __bool__ method can be used to override this behavior. If an object defines the __bool__ method, then Python calls that method to determine its truth value.
As an example, suppose we want the complex number 0 + 0 * i to be false. We can define the __bool__ method for both our complex number implementations.
>>> ComplexRI.__bool__ = lambda self: self.real != 0 or self.imag != 0 >>> ComplexMA.__bool__ = lambda self: self.magnitude != 0
We can call the bool constructor to see the truth value of an object, and we can use any object in a boolean context.
>>> bool(ComplexRI(1, 2))
True
>>> bool(ComplexRI(0, 0))
False
>>> if not ComplexMA(0, 1):
print("complex number is true")
complex number is true
Sequence length. We have seen that we can call the len function to determine the length of a sequence.
>>> len('Go Bears!')
9
The len function invokes the __len__ method of its argument to determine its length. All built-in sequence types implement this method.
>>> 'Go Bears!'.__len__() 9
Python uses a sequence's length to determine its truth value, if it does not provide a __bool__ method. Empty sequences are false, while non-empty sequences are true.
>>> bool('')
False
>>> bool([])
False
>>> bool('Go Bears!')
True
Callable objects. In Python, functions are first-class objects, so they can be passed around as data and have attributes like any other object. Python also allows us to define objects that can be "called" like functions by including a __call__ method. With this method, we can define a class that behaves like a higher-order function.
As an example, consider the following higher-order function, which returns a function that adds a constant value to its argument.
>>> def make_adder(n):
def adder(k):
return n + k
return adder
>>> add_three = make_adder(3) >>> add_three(4) 7
We can create an Adder class that defines a __call__ method to provide the same functionality.
>>> class Adder(object):
def __init__(self, n):
self.n = n
def __call__(self, k):
return self.n + k
>>> add_three_obj = Adder(3) >>> add_three_obj(4)
Here, the Adder class behaves like the make_adder higher-order function, and the add_three_obj object behaves like the add_three function. We have further blurred the line between data and functions.
Though callable objects are less efficient than higher-order functions, they allow us to take full advantage of the object system. For example, we can use inheritance to create a family of callable objects with shared functionality.
Further reading. Special methods generalize the built-in operators so that they can be used with user-defined objects. In order to provide this generality, Python follows specific protocols to apply each operator. For example, to evaluate expressions that contain the + operator, Python checks for special methods on both the left and right operands of the expression. First, Python checks for an __add__ method on the value of the left operand, then checks for an __radd__ method on the value of the right operand. If either is found, that method is invoked with the value of the other operand as its argument.
Similar protocols exist for evaluating expressions that contain any kind of operator in Python, including slice notation and Boolean operators. The Python docs list the exhaustive set of method names for operators. Dive into Python 3 has a chapter on special method names that describes many details of their use in the Python interpreter.
2.7.4 Generic Functions
Our implementation of complex numbers has made two data types interchangeable as arguments to the add_complex and mul_complex functions. Now we will see how to use this same idea not only to define operations that are generic over different representations but also to define operations that are generic over different kinds of arguments that do not share a common interface.
The operations we have defined so far treat the different data types as being completely independent. Thus, there are separate packages for adding, say, two rational numbers, or two complex numbers. What we have not yet considered is the fact that it is meaningful to define operations that cross the type boundaries, such as the addition of a complex number to a rational number. We have gone to great pains to introduce barriers between parts of our programs so that they can be developed and understood separately.
We would like to introduce the cross-type operations in some carefully controlled way, so that we can support them without seriously violating our abstraction boundaries. There is a tension between the outcomes we desire: we would like to be able to add a complex number to a rational number, and we would like to do so using a generic add function that does the right thing with all numeric types. At the same time, we would like to separate the concerns of complex numbers and rational numbers whenever possible, in order to maintain a modular program.
Let us revise our implementation of rational numbers to use Python's built-in object system. As before, we will store a rational number as a numerator and denominator in lowest terms.
>>> from fractions import gcd
>>> class Rational(object):
def __init__(self, numer, denom):
g = gcd(numer, denom)
self.numer = numer // g
self.denom = denom // g
def __repr__(self):
return 'Rational({0}, {1})'.format(self.numer, self.denom)
Adding and multiplying rational numbers in this new implementation is similar to before.
>>> def add_rationals(x, y):
nx, dx = x.numer, x.denom
ny, dy = y.numer, y.denom
return Rational(nx * dy + ny * dx, dx * dy)
>>> def mul_rationals(x, y):
return Rational(x.numer * y.numer, x.denom * y.denom)
Type dispatching. One way to handle cross-type operations is to design a different function for each possible combination of types for which the operation is valid. For example, we could extend our complex number implementation so that it provides a function for adding complex numbers to rational numbers. We can provide this functionality generically using a technique called dispatching on type.
The idea of type dispatching is to write functions that first inspect the type of argument they have received, and then execute code that is appropriate for the type. In Python, the type of an object can be inspected with the built-in type function.
>>> def iscomplex(z):
return type(z) in (ComplexRI, ComplexMA)
>>> def isrational(z):
return type(z) == Rational
In this case, we are relying on the fact that each object knows its type, and we can look up that type using the Python type function. Even if the type function were not available, we could imagine implementing iscomplex and isrational in terms of a shared class attribute for Rational, ComplexRI, and ComplexMA.
Now consider the following implementation of add, which explicitly checks the type of both arguments. We will not use Python's special methods (i.e., __add__) in this example.
>>> def add_complex_and_rational(z, r):
return ComplexRI(z.real + r.numer/r.denom, z.imag)
>>> def add(z1, z2):
"""Add z1 and z2, which may be complex or rational."""
if iscomplex(z1) and iscomplex(z2):
return add_complex(z1, z2)
elif iscomplex(z1) and isrational(z2):
return add_complex_and_rational(z1, z2)
elif isrational(z1) and iscomplex(z2):
return add_complex_and_rational(z2, z1)
else:
return add_rationals(z1, z2)
This simplistic approach to type dispatching, which uses a large conditional statement, is not additive. If another numeric type were included in the program, we would have to re-implement add with new clauses.
We can create a more flexible implementation of add by implementing type dispatch through a dictionary. The first step in extending the flexibility of add will be to create a tag set for our classes that abstracts away from the two implementations of complex numbers.
>>> def type_tag(x):
return type_tag.tags[type(x)]
>>> type_tag.tags = {ComplexRI: 'com', ComplexMA: 'com', Rational: 'rat'}
Here, we store the tag set as an attribute of the type_tag function to avoid polluting the global namespace. (Recall that functions are objects and therefore may have attributes.)
Next, we use these type tags to index a dictionary that stores the different ways of adding numbers. The keys of the dictionary are tuples of type tags, and the values are type-specific addition functions.
>>> def add(z1, z2):
types = (type_tag(z1), type_tag(z2))
return add.implementations[types](z1, z2)
This definition of add does not have any functionality itself; it relies entirely on a dictionary called add.implementations to implement addition. We can populate that dictionary as follows.
>>> add.implementations = {}
>>> add.implementations[('com', 'com')] = add_complex
>>> add.implementations[('com', 'rat')] = add_complex_and_rational
>>> add.implementations[('rat', 'com')] = lambda x, y: add_complex_and_rational(y, x)
>>> add.implementations[('rat', 'rat')] = add_rationals
This dictionary-based approach to dispatching is additive, because add.implementations and type_tag.tags can always be extended. Any new numeric type can "install" itself into the existing system by adding new entries to these dictionaries.
While we have introduced some complexity to the system, we now have a generic, extensible add function that handles mixed types.
>>> add(ComplexRI(1.5, 0), Rational(3, 2)) ComplexRI(3.0, 0) >>> add(Rational(5, 3), Rational(1, 2)) Rational(13, 6)
Data-directed programming. Our dictionary-based implementation of add is not addition-specific at all; it does not contain any direct addition logic. It only implements addition because we happen to have populated its implementations dictionary with functions that perform addition.
A more general version of generic arithmetic would apply arbitrary operators to arbitrary types and use a dictionary to store implementations of various combinations. This fully generic approach to implementing methods is called data-directed programming. In our case, we can implement both generic addition and multiplication without redundant logic.
>>> def apply(operator_name, x, y):
tags = (type_tag(x), type_tag(y))
key = (operator_name, tags)
return apply.implementations[key](x, y)
In this generic apply function, a key is constructed from the operator name (e.g., 'add') and a tuple of type tags for the arguments. Implementations are also populated using these tags. We enable support for multiplication on complex and rational numbers below.
>>> def mul_complex_and_rational(z, r):
return ComplexMA(z.magnitude * r.numer / r.denom, z.angle)
>>> mul_rationals_and_complex = lambda r, z: mul_complex_and_rational(z, r)
>>> apply.implementations = {('mul', ('com', 'com')): mul_complex,
('mul', ('com', 'rat')): mul_complex_and_rational,
('mul', ('rat', 'com')): mul_rationals_and_complex,
('mul', ('rat', 'rat')): mul_rationals}
We can also include the addition implementations from add to apply, using the dictionary update method.
>>> adders = add.implementations.items()
>>> apply.implementations.update({('add', tags):fn for (tags, fn) in adders})
Now that apply supports 8 different implementations in a single table, we can use it to manipulate rational and complex numbers quite generically.
>>> apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1)
This data-directed approach does manage the complexity of cross-type operators, but it is cumbersome. With such a system, the cost of introducing a new type is not just writing methods for that type, but also the construction and installation of the functions that implement the cross-type operations. This burden can easily require much more code than is needed to define the operations on the type itself.
While the techniques of dispatching on type and data-directed programming do create additive implementations of generic functions, they do not effectively separate implementation concerns; implementors of the individual numeric types need to take account of other types when writing cross-type operations. Combining rational numbers and complex numbers isn't strictly the domain of either type. Formulating coherent policies on the division of responsibility among types can be an overwhelming task in designing systems with many types and cross-type operations.
Coercion. In the general situation of completely unrelated operations acting on completely unrelated types, implementing explicit cross-type operations, cumbersome though it may be, is the best that one can hope for. Fortunately, we can sometimes do better by taking advantage of additional structure that may be latent in our type system. Often the different data types are not completely independent, and there may be ways by which objects of one type may be viewed as being of another type. This process is called coercion. For example, if we are asked to arithmetically combine a rational number with a complex number, we can view the rational number as a complex number whose imaginary part is zero. By doing so, we transform the problem to that of combining two complex numbers, which can be handled in the ordinary way by add_complex and mul_complex.
In general, we can implement this idea by designing coercion functions that transform an object of one type into an equivalent object of another type. Here is a typical coercion function, which transforms a rational number to a complex number with zero imaginary part:
>>> def rational_to_complex(x):
return ComplexRI(x.numer/x.denom, 0)
Now, we can define a dictionary of coercion functions. This dictionary could be extended as more numeric types are introduced.
>>> coercions = {('rat', 'com'): rational_to_complex}
It is not generally possible to coerce an arbitrary data object of each type into all other types. For example, there is no way to coerce an arbitrary complex number to a rational number, so there will be no such conversion implementation in the coercions dictionary.
Using the coercions dictionary, we can write a function called coerce_apply, which attempts to coerce arguments into values of the same type, and only then applies an operator. The implementations dictionary of coerce_apply does not include any cross-type operator implementations.
>>> def coerce_apply(operator_name, x, y):
tx, ty = type_tag(x), type_tag(y)
if tx != ty:
if (tx, ty) in coercions:
tx, x = ty, coercions[(tx, ty)](x)
elif (ty, tx) in coercions:
ty, y = tx, coercions[(ty, tx)](y)
else:
return 'No coercion possible.'
key = (operator_name, tx)
return coerce_apply.implementations[key](x, y)
The implementations of coerce_apply require only one type tag, because they assume that both values share the same type tag. Hence, we require only four implementations to support generic arithmetic over complex and rational numbers.
>>> coerce_apply.implementations = {('mul', 'com'): mul_complex,
('mul', 'rat'): mul_rationals,
('add', 'com'): add_complex,
('add', 'rat'): add_rationals}
With these implementations in place, coerce_apply can replace apply.
>>> coerce_apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> coerce_apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1.0)
This coercion scheme has some advantages over the method of defining explicit cross-type operations. Although we still need to write coercion functions to relate the types, we need to write only one function for each pair of types rather than a different functions for each collection of types and each generic operation. What we are counting on here is the fact that the appropriate transformation between types depends only on the types themselves, not on the particular operation to be applied.
Further advantages come from extending coercion. Some more sophisticated coercion schemes do not just try to coerce one type into another, but instead may try to coerce two different types each into a third common type. Consider a rhombus and a rectangle: neither is a special case of the other, but both can be viewed as quadrilaterals. Another extension to coercion is iterative coercion, in which one data type is coerced into another via intermediate types. Consider that an integer can be converted into a real number by first converting it into a rational number, then converting that rational number into a real number. Chaining coercion in this way can reduce the total number of coercion functions that are required by a program.
Despite its advantages, coercion does have potential drawbacks. For one, coercion functions can lose information when they are applied. In our example, rational numbers are exact representations, but become approximations when they are converted to complex numbers.
Some programming languages have automatic coercion systems built in. In fact, early versions of Python had a __coerce__ special method on objects. In the end, the complexity of the built-in coercion system did not justify its use, and so it was removed. Instead, particular operators apply coercion to their arguments as needed. Operators are implemented as method calls on user defined types using special methods like __add__ and __mul__. It is left up to you, the user, to decide whether to employ type dispatching, data-directed programming, message passing, or coercion in order to implement generic functions in your programs.