Due at 11:59pm on 07/12/2016.

Starter Files

Download lab06.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.

Submission

By the end of this lab, you should have submitted the lab with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be graded.

Questions 1, 2, and 3 must be completed in order to receive credit for this lab. Starter code for question 3 is in lab06.py.
Questions 4 and 5 (What Would Python Display?) are optional. It is recommended that you work on this should you finish the required section early, or if you are struggling with the required questions.
Questions 6 through 11 (Coding) are optional. It is recommended that you complete these problems on your own time. Starter code for these questions is in lab06_extra.py.

Helpful Hints

OK has a new feature for the "What would Python display?" questions. As you go through the question's prompts OK may give you a hint based on your wrong answers. Our hope is these hints will help remind you of something important or push you in the right direction to getting the correct answer. For example:

Foo > Suite 1 > Case 1
(cases remaining: 1)

What would Python display? If you get stuck, try it out in the Python
interpreter!

>>> not False or False
? False

-- Helpful Hint --
What about the | not |?
------------------

-- Not quite. Try again! --

?

Topics

Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the questions and refer back here should you get stuck.

Sequences

Sequences are ordered collections of values that support element-selection and have length. The most common sequence you've worked with are lists, but many other Python types are sequences as well, including strings.

Dictionaries

Dictionaries are unordered sets of key-value pairs. Keys can only be immutable types (strings, numbers, tuples), but their corresponding value can be anything! To create a dictionary, use the following syntax:

>>> singers = { 'Adele': 'Hello', 1975: 'Chocolate', 'The Weeknd': ['The Hills', 'Earned It'] }

The curly braces denote the key-value pairs in your dictionary. Each key-value pair is separated by a comma. For each pair, the key appears to the left of the colon and the value appears to the right of the colon. Note keys/values do not all have to be the same type, as you can see we have strings, integers and lists! Each key only appears once in a dictionary. You can retrieve values from your dictionary by "indexing" using the key:

>>> singers[1975]
'Chocolate'
>>> songs = singers['The Weeknd']
>>> songs[0]
'The Hills'

You can add an entry or update an entry for an existing key in the dictionary using the following syntax. Note they are identical syntax, so be careful!

>>> singers['Adele'] = 'Rolling in the Deep'
>>> singers['Adele']
'Rolling in the Deep'
>>> singers['Kanye West'] = 'Real Friends' # New entry!
>>> singers['Kanye West']
'Real Friends'

You can also check for membership of keys!

>>> 'Adele' in singers
True

Sets

A set is an unordered collection of distinct objects that supports membership testing, union, intersection, and adjunction. The main differences between sets and lists are that sets are unordered and contain no duplicates. Other than that, almost everything is the same.

>>> a = [1, 1, 2, 2, 3, 3]
>>> a = set(a)
>>> a  # No duplicates
{1, 2, 3}
>>> a = {3, 1, 2}
>>> a  # Not necessarily in same order
{1, 2, 3}

The Python documentation on sets has more details. The main things you will use with sets include: in, union (|), intersection (&), and difference (-).

Trees

A tree is a data structure that represents a hierarchy of information. A file system is a good example of a tree structure. For example, within your cs61a folder, you have folders separating your projects, lab assignments, and homework. The next level is folders that separate different assignments, hw01, lab01, hog, etc., and inside those are the files themselves, including the starter files and ok. Below is an incomplete diagram of what your cs61a directory might look like.

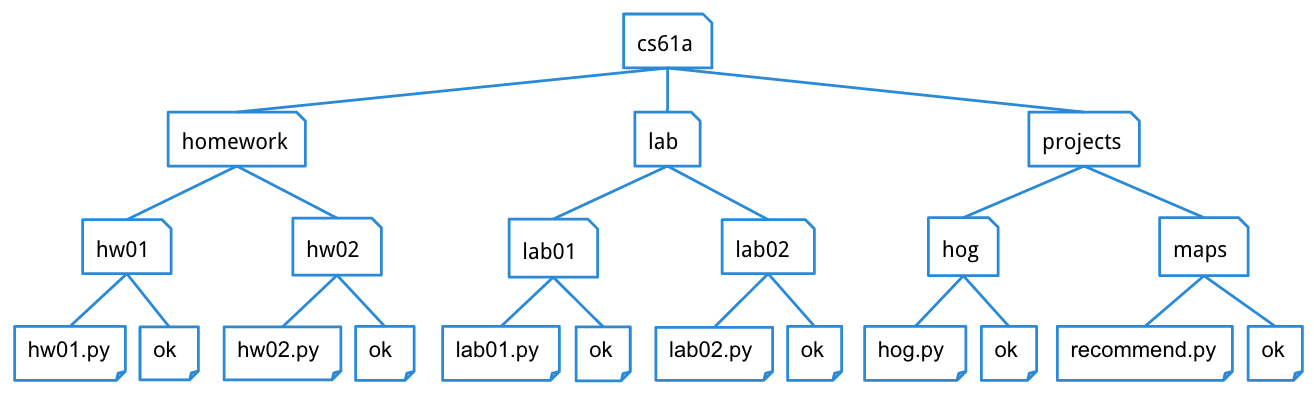
cs61a tree

As you can see, unlike trees in nature, the tree abstract data type is drawn with the root at the top and the leaves at the bottom.

Some tree terminology:

subtree: a smaller tree within the main tree
node: a unit that contains a single data value in a tree
root: the node at the top of a tree; every tree has one root node
entry: the value inside the root node of a tree
children: the subtrees directly under a tree's root; a child has its own root and possibly children of its own
leaf: a node that has no children

Our tree abstract data type consists of a root node and a list of its children. To create a tree and access its root and children, use the following constructor and selectors:

Constructor
- tree(entry, children=[]): creates a tree object with the given entry at its root and list of children.
Selectors
- entry(tree): returns the value in the root of tree.
- children(tree): returns the list of children of the given tree.
Convenience function
- is_leaf(tree): returns True if tree's list of children is empty, and False otherwise.

For example, the tree generated by

t = tree(1, [tree(2),
             tree(3, [tree(4), tree(5)]),
             tree(6, [tree(7)])])

would look like this:

It may be easier to visualize this translation by formatting the code like this:

t = tree(1,
         [tree(2),
          tree(3,
               [tree(4),
                tree(5)]),
          tree(6,
               [tree(7)])])

To extract the number 3 from this tree, which is the entry of the root of its second child, we would do this:

entry(children(t)[1])

The print_tree function prints out a tree in a human-readable form. The exact form follows the pattern illustrated above, where the root's label is unindented, and each of its children is indented one level further.

def print_tree(t, indent=0):
    """Print a representation of this tree in which each node is
    indented by two spaces times its depth from the entry.

    >>> print_tree(tree(1))
    1
    >>> print_tree(tree(1, [tree(2)]))
    1
      2
    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> print_tree(numbers)
    1
      2
      3
        4
        5
      6
        7
    """
    print('  ' * indent + str(entry(t)))
    for child in children(t):
        print_tree(child, indent + 1)

Required Questions

What Would Python Display?

Question 1: WWPD: Dictionaries

What would Python display? Type it in the intepreter if you're stuck!
python3 ok -q dicts -u

>>> pokemon = {'pikachu': 25, 'dragonair': 148, 'mew': 151}
>>> pokemon['pikachu']
______
25
>>> len(pokemon)
______
3
>>> pokemon['jolteon'] = 135
>>> pokemon['ditto'] = 25
>>> len(pokemon)
______
5
>>> sorted(list(pokemon.keys()))
______
['ditto', 'dragonair', 'jolteon', 'mew', 'pikachu']
>>> 'mewtwo' in pokemon
______
False
>>> pokemon['ditto'] = pokemon['jolteon']
>>> sorted(list(pokemon.keys()))
______
['ditto', 'dragonair', 'jolteon', 'mew', 'pikachu']
>>> pokemon['ditto']
______
135

>>> letters = {'a': 1, 'b': 2, 'c': 3}
>>> 2 in letters
______
False

>>> food = {'bulgogi': 10, 'falafel': 4, 'ceviche': 7}
>>> food['ultimate'] = food['bulgogi'] + food['ceviche']
>>> food['ultimate']
______
17
>>> len(food)
______
4
>>> food['ultimate'] += food['falafel']
>>> food['ultimate']
______
21
>>> sorted(list(food.keys()))
______
['bulgogi', 'ceviche', 'falafel', 'ultimate']
>>> food['bulgogi'] = food['falafel']
>>> len(food)
______
4
>>> 'gogi' in food
______
False

Question 2: Tree Structure

As described above, trees are constructed recursively with smaller subtrees using the constructor:

tree(label, children=[])

Test your understanding of how trees are constructed in Python by examining trees and deciding which of the choices of Python code matches that tree:
python3 ok -q structure -u

Coding Practice

Question 3: Map, Filter, Reduce

As an exercise, implement three functions map, filter, and reduce.

map takes in a one argument function fn and a sequence seq and returns a list containing fn applied to each element in seq.

filter takes in a predicate function pred and a sequence seq and returns a list containing all elements in seq for which pred returns True.

reduce takes in a two argument function combiner and a non-empty sequence seq and combines the elements in seq into one value using combiner.

def map(fn, seq):
    """Applies fn onto each element in seq and returns a list.

    >>> map(lambda x: x*x, [1, 2, 3])
    [1, 4, 9]
    """
    "*** YOUR CODE HERE ***"
    result = []
    for elem in seq:
        result += [fn(elem)]
    return result
def filter(pred, seq):
    """Keeps elements in seq only if they satisfy pred.

    >>> filter(lambda x: x % 2 == 0, [1, 2, 3, 4])
    [2, 4]
    """
    "*** YOUR CODE HERE ***"
    result = []
    for elem in seq:
        if pred(elem):
            result += [elem]
    return result
def reduce(combiner, seq):
    """Combines elements in seq using combiner.

    >>> reduce(lambda x, y: x + y, [1, 2, 3, 4])
    10
    >>> reduce(lambda x, y: x * y, [1, 2, 3, 4])
    24
    >>> reduce(lambda x, y: x * y, [4])
    4
    """
    "*** YOUR CODE HERE ***"
    total = seq[0]
    for elem in seq[1:]:
        total = combiner(total, elem)
    return total

Use OK to test your code:

python3 ok -q map
python3 ok -q filter
python3 ok -q reduce

Optional Questions

What Would Python Display?

Question 4: WWPD: Sets

Use OK to test your knowledge with the following "What Would Python Display?" questions:
python3 ok -q sets -u

>>> a = [1, 1, 2, 2, 3, 3]
>>> a = set(a)
>>> len(a)
______
3
>>> sorted(a)
______
[1, 2, 3]
>>> a.add(4)
>>> a.add(4)
>>> a.remove(4)
>>> 4 in a
______
False
>>> a = {1, 4, 12, 1000}
>>> sum(a)
______
1017
>>> b = {1, 2, 4}
>>> sorted(a.intersection(b))
______
[1, 4]
>>> sorted(a & b)
______
[1, 4]
>>> sorted(a.union(b))
______
[1, 2, 4, 12, 1000]
>>> sorted(a | b)
______
[1, 2, 4, 12, 1000]
>>> sorted(a - b)
______
[12, 1000]

>>> fruits = set(['apple', 'banana', 'tomato', 'apple'])
>>> pizza = set(['cheese', 'tomato', 'flour'])
>>> 'pepperoni' in pizza
______
False
>>> fruits & pizza
______
{'tomato'}

>>> t = [314, 15]
>>> u = {89, 7, 15}
>>> sorted(set(t) | u)
______
[7, 15, 89, 314]
>>> u.add(6)
>>> set(t) - u
______
{314}

Question 5: Height & Depth

The depth of a node in a tree is defined as the number of edges between that node and the root. The root has depth 0, its children have depth 1, and so on.

The height of a tree is the depth of the lowest leaf (furthest away from the root).

Test your understanding of depth and height with OK tests using the following command:
python3 ok -q height_depth -u

Shakespeare and Dictionaries

We will use dictionaries to approximate the entire works of Shakespeare! We're going to use a bigram language model. Here's the idea: We start with some word — we'll use "The" as an example. Then we look through all of the texts of Shakespeare and for every instance of "The" we record the word that follows "The" and add it to a list, known as the successors of "The". Now suppose we've done this for every word Shakespeare has used, ever.

Let's go back to "The". Now, we randomly choose a word from this list, say "cat". Then we look up the successors of "cat" and randomly choose a word from that list, and we continue this process. This eventually will terminate in a period (".") and we will have generated a Shakespearean sentence!

The object that we'll be looking things up in is called a "successor table", although really it's just a dictionary. The keys in this dictionary are words, and the values are lists of successors to those words.

Question 6: Successor Tables

Here's an incomplete definition of the build_successors_table function. The input is a list of words (corresponding to a Shakespearean text), and the output is a successors table. (By default, the first word is a successor to "."). See the example below.

Note: there are two places where you need to write code, denoted by the two "*** YOUR CODE HERE ***"

def build_successors_table(tokens):
    """Return a dictionary: keys are words; values are lists of
    successors.

    >>> text = ['We', 'came', 'to', 'investigate', ',', 'catch', 'bad', 'guys', 'and', 'to', 'eat', 'pie', '.']
    >>> table = build_successors_table(text)
    >>> sorted(table)
    [',', '.', 'We', 'and', 'bad', 'came', 'catch', 'eat', 'guys', 'investigate', 'pie', 'to']
    >>> table['to']
    ['investigate', 'eat']
    >>> table['pie']
    ['.']
    >>> table['.']
    ['We']
    """
    table = {}
    prev = '.'
    for word in tokens:
        if prev not in table:
            "*** YOUR CODE HERE ***"
            table[prev] = []
        "*** YOUR CODE HERE ***"
        table[prev] += [word]        prev = word
    return table

Use OK to test your code:

python3 ok -q build_successors_table

Question 7: Construct the Sentence

Let's generate some sentences! Suppose we're given a starting word. We can look up this word in our table to find its list of successors, and then randomly select a word from this list to be the next word in the sentence. Then we just repeat until we reach some ending punctuation.

Hint: to randomly select from a list, first make sure you import the Python random library with import random and then use the expression random.choice(my_list))

This might not be a bad time to play around with adding strings together as well. Let's fill in the construct_sent function!

def construct_sent(word, table):
    """Prints a random sentence starting with word, sampling from
    table.
    """
    import random
    result = ' '
    while word not in ['.', '!', '?']:
        "*** YOUR CODE HERE ***"
        result += word + ' '
        word = random.choice(table[word])
    return result + word

Use OK to test your code:

python3 ok -q construct_sent

Putting it all together

Great! Now all that's left is to run our functions with some actual code. The following snippet included in the skeleton code will return a list containing the words in all of the works of Shakespeare.

Warning: do NOT try to print the return result of this function.

def shakespeare_tokens(path='shakespeare.txt', url='http://composingprograms.com/shakespeare.txt'):
    """Return the words of Shakespeare's plays as a list."""
    import os
    from urllib.request import urlopen
    if os.path.exists(path):
        return open('shakespeare.txt', encoding='ascii').read().split()
    else:
        shakespeare = urlopen(url)
        return shakespeare.read().decode(encoding='ascii').split()

Next, we probably want an easy way to refer to our list of tokens and our successors table. Let's make the following assignments (Note: the following lines are commented in the provided file. Uncomment them before proceeding.)

# Uncomment the following two lines
# tokens = shakespeare_tokens()
# table = build_successors_table(tokens)

Finally, let's define an easy to call utility function:

>>> def sent():
...     return construct_sent('The', table)
>>> sent()
" The plebeians have done us must be news-cramm'd  ."

>>> sent()
" The ravish'd thee , with the mercy of beauty !"

>>> sent()
" The bird of Tunis , or two white and plucker down with better ; that's God's sake ."

Notice that all the sentences start with the word "The". With a few modications, we can make our sentences start with a random word. The following random_sent function (defined in your starter file) will do the trick:

def random_sent():
    import random
    return construct_sent(random.choice(table['.']), table)

Go ahead and load your file into Python (be sure to use the -i flag). You can now call the random_sent function to generate random Shakespearean sentences!

>>> random_sent()
' Long live by thy name , then , Dost thou more angel , good Master Deep-vow , And tak'st more ado but following her , my sight Of speaking false !'

>>> random_sent()
' Yes , why blame him , as is as I shall find a case , That plays at the public weal or the ghost .'

pyTunes Trees

The CS 61A staff has created a music library called pyTunes. pyTunes organizes songs in folders that are labeled by category — in other words, in a tree! The value at the root of the tree is your account name, which branches out into a hierarchy of categories: genres, artists, and albums, in that order. Songs (leaves in the tree) can be stored at any of these levels. A category cannot be empty (i.e. there will never be a node for a genre, artist, or album with no branches).

Question 8: Create pyTunes

All pyTunes accounts come with the free songs below. Define the function make_pytunes, which takes in username and creates this tree:

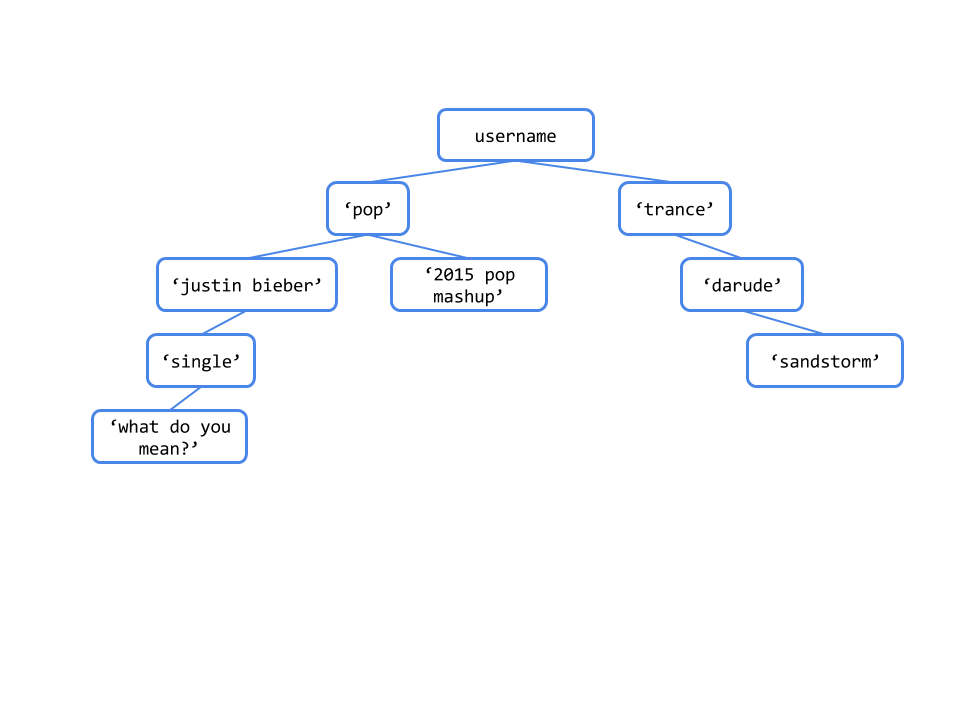
pytunes tree

The doctest below shows the print_tree representation of a default pyTunes tree.

def make_pytunes(username):
    """Return a pyTunes tree as shown in the diagram with USERNAME as the value
    of the root.

    >>> pytunes = make_pytunes('i_love_music')
    >>> print_tree(pytunes)
    i_love_music
      pop
        justin bieber
          single
            what do you mean?
        2015 pop mashup
      trance
        darude
          sandstorm
    """
    "*** YOUR CODE HERE ***"
    return tree(username, 
             [tree('pop', 
               [tree('justin bieber',
                 [tree('single',
                   [tree('what do you mean?')])]),
                tree('2015 pop mashup')]),
              tree('trance',
                [tree('darude', 
                  [tree('sandstorm')])])])

Use OK to test your code:

python3 ok -q make_pytunes

Question 9: Number of Songs

A pyPod can only hold 10 songs, and you need to find out whether or not all the songs in your pyTunes account will fit. Define the function num_songs, which takes in a pyTunes tree t and returns the number of songs in t. Recall that there are no empty directories in pyTunes, so all leaves in t are songs.

Hint: You can use is_leaf to check whether a given tree is a leaf.

>>> no_branches = tree(1)
>>> is_leaf(no_branches)
True
>>> is_leaf(tree(5, [tree(3), tree(4)]))
False

def num_songs(t):
    """Return the number of songs in the pyTunes tree, t.

    >>> pytunes = make_pytunes('i_love_music')
    >>> num_songs(pytunes)
    3
    """
    "*** YOUR CODE HERE ***"
    if is_leaf(t):
        return 1
    return sum([num_songs(b) for b in children(t)])

# Alternate solution
def num_songs(t):
    if is_leaf(t):
        return 1
    leaves = 0
    for b in children(t):
        leaves += num_songs(b)
    return leaves

Use OK to test your code:

python3 ok -q num_songs

Question 10: Add Song

Of course, you should be able to add music to your pyTunes. Write add_song to add song to the given category. You should not be able to add a song under a song or to a category that doesn't exist. See the doctests for examples.

def add_song(t, song, category):
    """Returns a new tree with SONG added to CATEGORY. Assume the CATEGORY
    already exists.

    >>> indie_tunes = tree('indie_tunes',
    ...                  [tree('indie',
    ...                    [tree('vance joy',
    ...                       [tree('riptide')])])])
    >>> new_indie = add_song(indie_tunes, 'georgia', 'vance joy')
    >>> print_tree(new_indie)
    indie_tunes
      indie
        vance joy
          riptide
          georgia

    """
    "*** YOUR CODE HERE ***"
    if root(t) == category:
        return tree(root(t), children(t) + [tree(song)])
    kept_children = []
    for b in children(t):
        kept_children += [add_song(b, song, category)]
    return tree(root(t), kept_children)

# Alternative Solution
def add_song(t, song, category):
    if root(t) == category:
        return tree(root(t), children(t) + [tree(song)])
    all_children = [add_song(b, song, category) for b in children(t)]
    return tree(root(t), all_children)

Use OK to test your code:

python3 ok -q add_song

Question 11: Delete

You also want to be able to delete a song or category from your pyTunes. Define the function delete, which takes in a pyTunes tree t and returns a new tree that is the same as t except with target deleted. If target is a genre, artist, or album, delete everything inside of it. It should not be possible to delete the entire account or root of the tree. Deleting all the songs within a category should not remove that category.

def delete(t, target):
    """Returns the tree that results from deleting TARGET from t. If TARGET is
    a category, delete everything inside of it.

    >>> my_account = tree('kpop_king',
    ...                    [tree('korean',
    ...                          [tree('gangnam style'),
    ...                           tree('wedding dress')]),
    ...                     tree('pop',
    ...                           [tree('t-swift',
    ...                                [tree('blank space')]),
    ...                            tree('uptown funk'),
    ...                            tree('see you again')])])
    >>> new = delete(my_account, 'pop')
    >>> print_tree(new)
    kpop_king
      korean
        gangnam style
        wedding dress
    """
    "*** YOUR CODE HERE ***"
    kept_children = []
    for b in children(t):
        if root(b) != target:
            kept_children += [delete(b, target)]
    return tree(root(t), kept_children)

# Alternate solution
def delete(t, target): 
    kept_children = [delete(b, target) for b in children(t) if root(b) != target]
    return tree(root(t), kept_children)

Use OK to test your code:

python3 ok -q delete

Lab 6: Trees and Mutable Sequences

Starter Files

Submission

Helpful Hints

Topics

Sequences

Dictionaries

Sets

Trees

Required Questions

What Would Python Display?

Question 1: WWPD: Dictionaries

Question 2: Tree Structure

Coding Practice

Question 3: Map, Filter, Reduce

Optional Questions

What Would Python Display?

Question 4: WWPD: Sets

Question 5: Height & Depth

Shakespeare and Dictionaries

Question 6: Successor Tables

Question 7: Construct the Sentence

Putting it all together

pyTunes Trees

Question 8: Create pyTunes

Question 9: Number of Songs

Question 10: Add Song

Question 11: Delete