Homework 7
Due by 11:59pm on Monday, 7/24
Instructions
Download hw07.zip.
Submission: When you are done, submit with
python3 ok --submit.
You may submit more than once before the deadline; only the final submission
will be scored. Check that you have successfully submitted your code on
okpy.org.
See Lab 0
for more instructions on submitting assignments.
Using OK: If you have any questions about using OK, please refer to this guide.
Homework Questions
Linked Lists
Question 1: Every Other
Implement every_other, which takes a linked list s. It mutates s such
that all of the odd-indexed elements (using 0-based indexing) are removed from
the list. For example:
>>> s = Link('a', Link('b', Link('c', Link('d'))))
>>> every_other(s)
>>> s.first
'a'
>>> s.rest.first
'c'
>>> s.rest.rest is Link.empty
TrueIf s contains fewer than two elements, s remains unchanged.
Do not return anything!
every_othershould mutate the original list.
def every_other(s):
"""Mutates a linked list so that all the odd-indiced elements are removed
(using 0-based indexing).
>>> s = Link(1, Link(2, Link(3, Link(4))))
>>> every_other(s)
>>> s
Link(1, Link(3))
>>> odd_length = Link(5, Link(3, Link(1)))
>>> every_other(odd_length)
>>> odd_length
Link(5, Link(1))
>>> singleton = Link(4)
>>> every_other(singleton)
>>> singleton
Link(4)
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q every_otherQuestion 2: Mutable Mapping
Implement deep_map_mut(fn, link), which applies a function fn onto
all elements in the given linked list link. If an element is itself a
linked list, apply fn to each of its elements, and so on.
Your implementation should mutate the original linked list. Do not create any new linked lists.
Hint: The built-in
isinstancefunction may be useful.>>> s = Link(1, Link(2, Link(3, Link(4)))) >>> isinstance(s, Link) True >>> isinstance(s, int) False
def deep_map_mut(fn, link):
"""Mutates a deep link by replacing each item found with the
result of calling fn on the item. Does NOT create new Links (so
no use of Link's constructor)
Does not return the modified Link object.
>>> link1 = Link(3, Link(Link(4), Link(5, Link(6))))
>>> deep_map_mut(lambda x: x * x, link1)
>>> print_link(link1)
<9 <16> 25 36>
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q deep_map_mutQuestion 3: Two List
Implement a function two_list that takes in two lists and returns a linked list. The first list contains the
values that we want to put in the linked list, and the second list contains the number of each corresponding value.
Assume both lists are the same size and have a length of 1 or greater. Assume all elements in the second list
are greater than 0.
def two_list(lst1, lst2):
"""
Returns a linked list according to the two lists that were passed in. Assume
lst1 and lst2 are the same size. Elements in lst1 represent the value, and the
corresponding element in lst2 represents the number of this value is desired in the
final linked list. Assume all elements in lst2 are greater than 0. Assume both
lists have at least one element.
>>> a = [1, 3, 2]
>>> b = [1, 1, 1]
>>> c = two_list(a, b)
>>> c
Link(1, Link(3, Link(2)))
>>> a = [1, 3, 2]
>>> b = [2, 2, 1]
>>> c = two_list(a, b)
>>> c
Link(1, Link(1, Link(3, Link(3, Link(2)))))
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q two_listQuestion 4: Cycles
The Link class can represent lists with cycles. That is, a list may
contain itself as a sublist.
>>> s = Link(1, Link(2, Link(3)))
>>> s.rest.rest.rest = s
>>> s.rest.rest.rest.rest.rest.first
3Implement has_cycle,that returns whether its argument, a Link
instance, contains a cycle.
Hint: Iterate through the linked list and try keeping track of which
Linkobjects you've already seen.
def has_cycle(link):
"""Return whether link contains a cycle.
>>> s = Link(1, Link(2, Link(3)))
>>> s.rest.rest.rest = s
>>> has_cycle(s)
True
>>> t = Link(1, Link(2, Link(3)))
>>> has_cycle(t)
False
>>> u = Link(2, Link(2, Link(2)))
>>> has_cycle(u)
False
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q has_cycleExtra question: This question is not worth extra credit and is entirely optional. It is designed to challenge you to think creatively!
Implement has_cycle_constant with only constant space. (If you followed
the hint above, you will use linear space.) The solution is short (less than 20
lines of code), but requires a clever idea. Try to discover the solution
yourself before asking around:
def has_cycle_constant(link):
"""Return whether link contains a cycle.
>>> s = Link(1, Link(2, Link(3)))
>>> s.rest.rest.rest = s
>>> has_cycle_constant(s)
True
>>> t = Link(1, Link(2, Link(3)))
>>> has_cycle_constant(t)
False
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q has_cycle_constantTrees
Question 5: Cumulative Sum
Write a function cumulative_sum that mutates the Tree t, where each node's
root becomes the sum of all entries in the subtree rooted at the node.
def cumulative_sum(t):
"""Mutates t where each node's root becomes the sum of all entries in the
corresponding subtree rooted at t.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> cumulative_sum(t)
>>> t
Tree(16, [Tree(8, [Tree(5)]), Tree(7)])
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q cumulative_sumQuestion 6: Prune Min
Write a function that prunes a tree t mutatively. Tree t and its branches always have zero branches or two branches. For the trees with two branches, reduce the number of branches from two to one by keeping the branch that has the smaller root value. Do nothing with trees with zero branches. Prune the tree from the bottom up. The result should be a linear tree.
def prune_min(t):
"""Prune the tree mutatively from the bottom up. Assume the tree and its branches always have either two branches or none. Prune the tree by
reducing the number of branches from two to one, choosing the branch with the smaller root value. Assume branches have differing root values.
Do nothing with trees with zero branches.
>>> t1 = Tree(6)
>>> prune_min(t1)
>>> t1
Tree(6)
>>> t2 = Tree(6, [Tree(3), Tree(4)])
>>> prune_min(t2)
>>> t2
Tree(6, [Tree(3)])
>>> t3 = Tree(6, [Tree(3, [Tree(1), Tree(2)]), Tree(5, [Tree(3), Tree(4)])])
>>> prune_min(t3)
>>> t3
Tree(6, [Tree(3, [Tree(1)])])
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q prune_minQuestion 7: Long Paths
Implement long_paths, which returns a list of all paths in a tree with
length at least n. A path in a tree is a linked list of node values that
starts with the root and ends at a leaf. Each subsequent element must be from a
child of the previous value's node. The length of a path is the number of
edges in the path (i.e. one less than the number of nodes in the path).
Paths are listed in order from left to right.
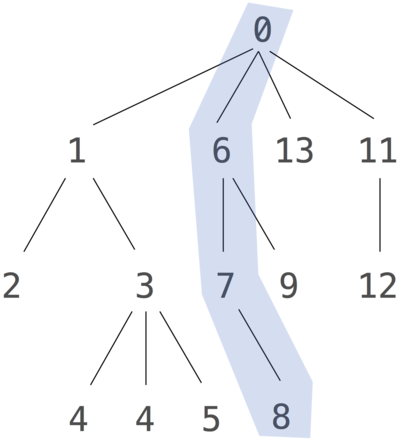
def long_paths(tree, n):
"""Return a list all paths in tree with length at least n.
>>> t = Tree(3, [Tree(4), Tree(4), Tree(5)])
>>> left = Tree(1, [Tree(2), t])
>>> mid = Tree(6, [Tree(7, [Tree(8)]), Tree(9)])
>>> right = Tree(11, [Tree(12)])
>>> whole = Tree(0, [left, Tree(13), mid, right])
>>> for path in long_paths(whole, 2):
... print(path)
...
Link(0, Link(1, Link(2)))
Link(0, Link(1, Link(3, Link(4))))
Link(0, Link(1, Link(3, Link(4))))
Link(0, Link(1, Link(3, Link(5))))
Link(0, Link(6, Link(7, Link(8))))
Link(0, Link(6, Link(9)))
Link(0, Link(11, Link(12)))
>>> for path in long_paths(whole, 3):
... print(path)
...
Link(0, Link(1, Link(3, Link(4))))
Link(0, Link(1, Link(3, Link(4))))
Link(0, Link(1, Link(3, Link(5))))
Link(0, Link(6, Link(7, Link(8))))
>>> long_paths(whole, 4)
[]
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q long_paths