Lab 10: Scheme
Due at 11:59pm on Tuesday, 7/25/2017.
Starter Files
Download lab10.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
- To receive credit for this lab, you must complete Questions 1 through 5 in lab10.scm and submit through OK.
- Questions 6 through 9 are extra practice. They can be found in the lab10_extra.scm file. It is recommended that you complete these problems on your own time.
Scheme
Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses a prefix notation and (often many) nested parentheses (see http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.
Our course uses a custom version of Scheme (which you will build for Project 4) included in the starter ZIP archive. To start the interpreter, type
python3 scheme. To run a Scheme program interactively, typepython3 scheme -i <file.scm>. To exit the Scheme interpreter, type(exit).You can load a file into Scheme using the following command (replace
name_of_filewith the name of your file):python3 scheme -load name_of_file.scmThis is like
python3 -i name_of_file.py.
You may find it useful to try scheme.cs61a.org when working through problems, as it can draw environment and box-and-pointer diagrams and it lets you walk your code step-by-step (similar to Python Tutor). Don't forget to submit your code through OK though!
Control Structures
If Expressions
Let's introduce control expressions to allow our procedures to do more complex operations! The if-expression has the following format:
(if <condition>
<true_result>
<false_result>)For example, the following code written in Scheme and Python are equivalent:
| Scheme | Python |
|---|---|
|
|
In Scheme, you cannot write elif cases. If want to have multiple cases with the if-expression, you would need multiple branched if-expressions:
| Scheme | Python |
|---|---|
|
|
Cond Expressions
Using nested if-expression doesn't seem like a very practical way to take care of multiple cases. Instead, we can use the cond special form, a general conditional expression similar to a multi-clause conditional expression in Python.
(cond
(<p1> <e1>)
(<p2> <e2>)
...
(<pn> <en>)
(else <else-expression>))It consists of the symbol cond followed by pairs of expressions enclosed in parentheses (<p> <e>) called clauses. The first expression in each pair is a predicate: an expression whose value is interpreted as either True or False. The second expression is the return expression corresponding to its predicate.
The following code is equivalent:
| Scheme | Python |
|---|---|
|
|
Question 1: Over or Under
Define a procedure over-or-under which takes in an x and a y and
returns the the following:
- return -1 if
xis less thany - return 0 if
xis equal toy - return 1 if
xis greater thany
(define (over-or-under x y)
'YOUR-CODE-HERE
(cond
((< x y) -1)
((= x y) 0)
(else 1)))
;;; Tests
(over-or-under 1 2)
; expect -1
(over-or-under 2 1)
; expect 1
(over-or-under 1 1)
; expect 0Use OK to test your code:
python3 ok -q over-or-underLists
Scheme Pairs
Scheme lists are very similar to the linked lists we've been working with in
Python. Scheme lists are made up of pairs, which can point to two objects. To
create a pair, we use the cons procedure, which takes in two arguments:
scm> (define a (cons 3 5))
a
scm> a
(3 . 5)We can use the car and cdr procedures to retrieve the first and second
elements in the pair, respectively.
scm> (car a)
3
scm> (cdr a)
5Just like linked lists in Python, lists in Scheme are formed by having the
first element of a pair be the first element of the list, and the second
element of the pair point to another pair containing the rest of the list. The
second element of a pair can be nil to signify the end of the list. For
example, the sequence (1 2 3) can be represented in Scheme with the following
line:
scm> (cons 1 (cons 2 (cons 3 nil)))which creates the following object in Scheme:

We can then of course retrieve values from our list with the car and cdr
procedures. (Curious about where these weird names come from?
Check out their etymology.)
scm> a
(1 2 3)
scm> (car a)
1
scm> (cdr a)
(2 3)
scm> (car (cdr (cdr a)))
3list
There are a few other ways to create lists. We can pass a sequence of
arguments into the list procedure, which quickly constructs a well-formed list
(one in which the cdr of every pair is either another pair or nil):
scm> (list 1 2 3)
(1 2 3)Quote Form
We can also use the quote form to create a list, which performs much the same
functionality as the list procedure. Unlike list, we can use the quote
form to construct a malformed list. Notice that we can use a dot to separate
the car and the cdr of a pair, but Scheme will only show us the dot if the
list is malformed:
scm> '(1 2 3)
(1 2 3)
scm> '(1 . (2 . (3)))
(1 2 3)
scm> '(1 . (2 . 3))
(1 2 . 3)Built-In Procedures for Lists
There are a few other built-in procedures in Scheme that are used for lists. Try them out!
scm> (null? nil)
______True
scm> (append '(1 2 3) '(4 5 6))
______(1 2 3 4 5 6)
scm> (cons '(1 2 3) '(4 5 6))
______((1 2 3) 4 5 6)
scm> (list '(1 2 3) '(4 5 6))
______((1 2 3) (4 5 6))
scm> (length '(1 2 3 4 5))
______5Question 2: WWSD: Lists
Use OK to test your knowledge with the following "What Would Scheme Print?" questions:
python3 ok -q wwsd-lists -u
Question 3: Make a List
Create the list with the following box-and-pointer diagram:
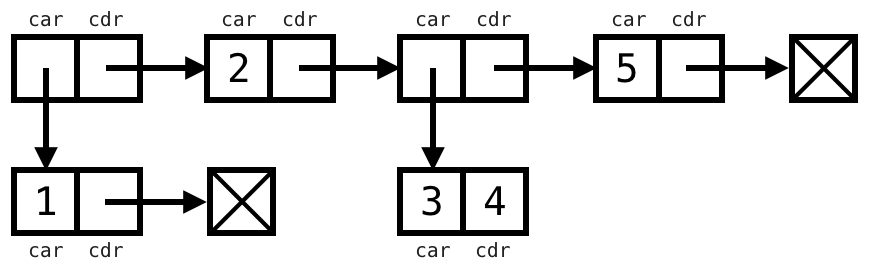
(define lst
'YOUR-CODE-HERE
(cons (cons 1 '())
(cons 2
(cons (cons 3 4)
(cons 5 '())))))Use OK to test your code:
python3 ok -q make-listQuestion 4: Filter
Write a procedure filter, which takes a predicate f and a list lst, and
returns a new list containing only elements of the list that satisfy the
predicate.
(define (filter f lst)
'YOUR-CODE-HERE
(cond ((null? lst) '())
((f (car lst)) (cons (car lst) (filter f (cdr lst))))
(else (filter f (cdr lst)))))
;;; Tests
(define (even? x)
(= (modulo x 2) 0))
(filter even? '(0 1 1 2 3 5 8))
; expect (0 2 8)Use OK to test your code:
python3 ok -q filterLambdas
Ah yes, you thought you were safe, but we can also write lambda
procedures in Scheme!
As noted above, the syntax for defining a procedure in Scheme is:
(define (<name> <params>)
<body>
)Defining a lambda has a slightly different syntax, as follows:
(lambda (<params>)
<body>
)Notice how the only difference is the lack of procedure name. You can create and call a lambda procedure in Scheme as follows:
; defining a lambda
(lambda (x) (+ x 3))
; calling a lambda
((lambda (x) (+ x 3)) 7)Question 5: Make Adder
Write the procedure make-adder which takes in an initial number,
num, and then returns a procedure. This returned procedure takes in a
number x and returns the result of x + num.
(define (make-adder num)
'YOUR-CODE-HERE
(lambda (x) (+ x num)))
;;; Tests
(define adder (make-adder 5))
(adder 8)
; expect 13Use OK to test your code:
python3 ok -q make-adderExtra Questions
The following questions are for extra practice -- they can be found in the the lab10_extra.scm file. It is recommended that you complete these problems on your own time.
Question 6: Remove
Implement a procedure remove that takes in a list and returns a new list with
all instances of item removed from lst. You may assume the list will only
consists of numbers and will not have nested lists.
Hint: You might find the filter procedure useful.
(define (remove item lst)
'YOUR-CODE-HERE
(cond ((null? lst) '())
((equal? item (car lst)) (remove item (cdr lst)))
(else (cons (car lst) (remove item (cdr lst))))))
(define (remove item lst)
(filter (lambda (x) (not (= x item))) lst))
;;; Tests
(remove 3 nil)
; expect ()
(remove 3 '(1 3 5))
; expect (1 5)
(remove 5 '(5 3 5 5 1 4 5 4))
; expect (3 1 4 4)Use OK to test your code:
python3 ok -q removeQuestion 7: Compose
Write the procedure composed, which takes in procedures f and g
and outputs a new procedure. This new procedure takes in a number x
and outputs the result of calling f on g of x.
(define (composed f g)
'YOUR-CODE-HERE
(lambda (x) (f (g x))))Use OK to test your code:
python3 ok -q composedQuestion 8: Greatest Common Divisor
Let's revisit a familiar problem: finding the greatest common divisor of two numbers.
Write the procedure gcd, which computes the gcd of numbers a and b.
Recall that the greatest common divisor of two positive integers a and b
is the largest integer which evenly divides both numbers (with no remainder).
Euclid's
algorithm states
that the greatest common divisor is
- the smaller value if it evenly divides the larger value, OR
- the greatest common divisor of the smaller value and the remainder of the larger value divided by the smaller value
In other words, if a is greater than b and a is not divisible by
b, then
gcd(a, b) == gcd(b, a % b)You may find the provided procedures min and max helpful. You can
also use the built-in modulo procedure.
(define (max a b) (if (> a b) a b))
(define (min a b) (if (> a b) b a))
(define (gcd a b)
'YOUR-CODE-HERE
(cond ((zero? a) b)
((zero? b) a)
(else (gcd (min a b) (modulo (max a b) (min a b))))))
;;; Tests
(gcd 24 60)
; expect 12
(gcd 1071 462)
; expect 21Use OK to test your code:
python3 ok -q gcdQuestion 9: Split
Implement split-at, which takes a list lst and a positive number n as
input and returns a pair new such that (car new) is the first n
elements of lst and (cdr new) is the remaining elements of lst. If n is
greater than the length of lst, (car new) should be lst and (cdr new)
should be nil.
(define (split-at lst n)
'YOUR-CODE-HERE
(cond ((= n 0) (cons nil lst))
((null? lst) (cons lst nil))
(else (let ((rec (split-at (cdr lst) (- n 1))))
(cons (cons (car lst) (car rec)) (cdr rec))))))Use OK to test your code:
python3 ok -q split-at