Graph is a powerful and fundamental data abstraction in computer science. It is made up of vertices and edges. Graphs can be used to represent many things: network connections, dependencies, image compositions, state machines, artificial neural networks, etc. It is critical for you understand graphs if you want to pursue a future in computer science - whether that's research or industry. We will explore some of the most basic graph algorithms today, namely breadth first search (BFS), depth first search (DFS), and A star (A*) algorithm for shortest path.
A. Introduction to our Maze Solver
In this lab, we'll explore how various graph algorithms behave in the context of mazes, like the one shown below.
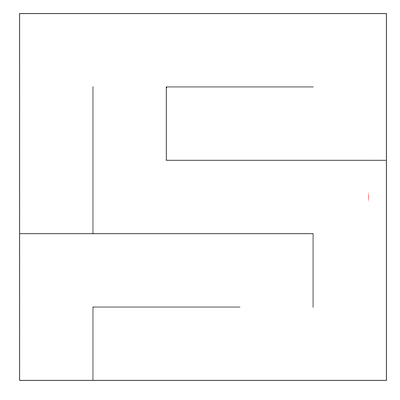
One way to represent a maze is as an undirected graph. The vertices of such a graph are shown below, with one dimensional (vertex number) coordinates on the left version and X/Y coordinates on the right version. If there is no wall between two adjacent vertices, then the corresponding graph has an undirected edge between the vertices. For example, adj(11) would be an iterable containing the integers 12 and 16.


In this lab, you'll implement a few key graph algorithms using the provided Maze class, which has the following methods of interest:
public int N(): Size of the maze (mazes are N x N)
public int V(): Total number of vertices in the maze
public Iterable<Integer> adj(int v): Returns the neighbors of v
public int toX(int v): Returns the x coordinate of vertex v
public int toY(int v): Returns the y coordinate of vertex v
public int xyTo1D(int x, int y): Returns the vertex number of x, yWe've provided MazeDepthFirstPaths, a version of DepthFirstPaths adapted for use with mazes. For official lab credit, you'll need to implement at least an adaptation of BreadthFirstPaths and the cycle detection algorithm, MazeCycles. For those of you want a deeper understanding of graph algorithms, we've also provided a challenge to implement the A* shortest paths algorithm. Specifically, you'll end up with:
MazeDepthFirstPaths.java: Uses DFS to find all paths from a given source, terminating as soon as the target vertex is observed. Provided for you.MazeBreadthFirstPaths.java: Uses BFS to find all paths from a given source, terminating as soon as the target vertex is observed.MazeCycles.java: Searches for cycles in the maze. If a cycle is detected, the algorithm terminates.AStarPath.java: Searches for the shortest path from source to a target using A*, terminating when the target is observed.
These four maze solvers should be subclasses of the abstract MazeExplorer class, which has the following fields and methods:
public boolean[] marked: Locations to mark in blue
public int[] distTo: Distances to draw over the Maze
public int[] edgeTo: Edges to draw on Maze
public Maze maze: The maze being solved
public void announce(): Call whenever you want the drawing updated
public solve(): Solves the given Maze problemThe Maze class has special functionality built in so that it can see your MazeExplorer's public variables. Specifically, whenever you call announce, it will draw the contents of your MazeExplorer's marked, distTo, and edgeTo arrays. Make sure to call the announce method any time you want the drawing to be updated.
As an example, try compiling and running TrivialMazeExplorerDemo.java. Open up the TrivialMazeExplorer and TrivialMazeExplorerDemo files to understand what's going on.
To compile, simply run make in the lab directory with all the Java files. To run a particular demo, say TrivialMazeExplorerDemo, execute java TrivialMazeExplorerDemo in command line.
As a more complex example, try compiling and running DepthFirstDemo. This code was adapted from the DepthFirstPaths class that was discussed during lecture.
If you want to tweak the parameters of the maze, you can edit the maze.config file. There are three different types of mazes (SINGLE_GAP, POPEN_SOLVABLE, and BLANK) to choose from. A % sign at the beginning of a line in the config file comments it out.
B. Breadth First Search
BFS and DFS are very similar. BFS uses a queue (FIFO) to store the fringe, whereas DFS uses a stack (FILO). Naturally, programmers often use recursion for DFS, since we can take advantage of and use the implicit recursive call stack as our fringe. For BFS? There are no implicit structures that we can use. We must use a loop to simulate the expansion of the fringe.
You will need to use a FIFO queue for this part. Luckily, Java's powerful library already has a Queue interface (a sub-interface of the almighty Collection interface) built in. Read the interface documentation carefully. Hint! See if you can sight any familiar Collection implementing class that also implements this Queue interface. Feel free to use any of them.
You'll now write a class MazeBreadthFirstPaths.java that extends MazeExplorer. You should use MazeDepthFirstPaths as inspiration. When you compile and run BreadthFirstDemo.java, you should see your algorithm crawl the graph, locating the shortest path from position (1, 1) to (N, N), stopping as soon as the (N, N) position is found.
You should use BreadthFirstPaths as inspiration.
Professor Hug had put together a quick video showcasing the expected behavior of each class, though there's a small bug in MazeBreadthFirstPaths that he pointed out during the video.
C. Depth First Search & Cycle Check
In the world of graph theory, there exist many cycle detection algorithms. Union-find algorithm can detect cycle in O(E*logV). For today's exercise, we will use DFS to detect cycles in this maze (undirected graph) in O(E+V). For every visited vertex v, if there is an adjacent u such that u is already visited and u is not parent of v, then there is a cycle in graph.
For this part of the lab, you'll write a cycle detection algorithm. When you compile and run CylesDemo, you should see your algorithm crawl the graph. If it identifies any cycles, it should connected the vertices of the cycle using purple lines (by setting values in the edgeTo array and calling announce()).
Recall from last section, you can use either recursion or a Stack class for DFS. If you decide to go with latter, you need to look up the Java Stack class, or use some linear structure in a FILO fashion.
D. A* (optional, but worth a read)
In graph theory, shortest path between two nodes is one of the most common and important questions asked. This problem has many real world analogies; shortest route between two cities is the most overused one in computer science. Dijkstra's algorithm is the most basic shortest path algorithm. It can find the shortest path between two points assuming no negative edge weights. Dijkstra's is very similar to BFS. Replace the queue in BFS with a priority queue (with some more minor tweaks) and we now have Dijkstra's!
However, Dijkstra's algorithm is a uniform-cost search. If we want to find the shortest path from SF to NYC, Dijkstra's will expand in all directions centered at SF. The fringe will reach Seattle before even getting close to the East coast. We can make it "smarter" by giving it a heuristic.
Introducing A* (A star) search! A* is the state-of-the-art shortest path finding algorithm (if the programmer provides it a good heuristic) (e.g. Manhattan distance to destination). Back to the SF to NYC path finding analogy, A* will prioritize moving to the East first, since our heuristic will tell it that moving straight up toward Seattle (going to Canada?) is bad compared to moving toward Denver (closer to NYC).
Here is a nice visualization for BFS, DFS, Dijkstra's algorithm, and A* algorithm. I highly recommend playing around with it to improve your understanding of these most basic graph algorithms.
For this part of the lab, you'll implement the A* algorithm. When you compile and run AStarDemo, you should see your algorithm crawl the graph, seeking the shortest path from (1, 1) to (N, N). Unlike BFS, the algorithm should take into account the target vertex.
For your heuristic h(v), I recommend that you use the Manhattan distance, which can be simply expressed as:
Math.abs(sourceX - targetX) + Math.abs(sourceY - targetY);Experiment with different graph types and heuristics to see how they behave.
Submission
You need to submit MazeBreadthFirstPaths.java and MazeCycles.java. MazeAStarPath.java is optional. Make sure to run BreadthFirstDemo and CyclesDemo, and make sure they function correctly before you submit.