Optional online warm-up problemsWe suggest that you work through at least some of these before starting on the homework itself. Since it will help solidify your basic knowledge of the material, you should find that it reduces confusion (and hopefully time spent) on the homework itself. Give it a try and see if it helps you. If nothing else, they're good study material!You can find some study materials for the final here. |
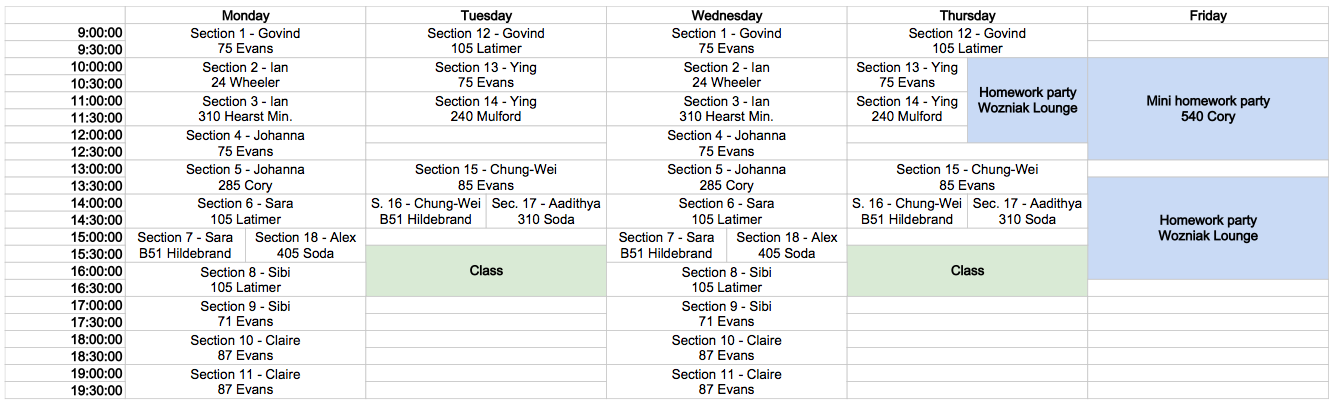
Every week in the Wozniak Lounge, there will be a "homework party." This is completely optional. GSIs will be present in shifts as will some readers. Students are expected to help each other out, and if desired, form ad-hoc "pickup" homework groups in the style of a pickup basketball game.
The Woz is a relatively big space and if the weather is nice, we can also access the patio outside. But if the room is crowded, excercise good judgement and make room for others by leaving if you can find an alternative source of assistance. When the room is not crowded, people from the class are welcome to just hang out as long as they aren't bothering other people. Some social games might be available.
This is an experiment. For it to succeed, you all have to be very responsible in taking care of the room, not making messes, and putting things back the way they were.
Discrete mathematics and probability theory provide the foundation for many algorithms, concepts, and techniques in the field of Electrical Engineering and Computer Sciences. For example, computer hardware is based on Boolean logic. Induction is closely tied to recursion and is widely used, along with other proof techniques, in theoretical arguments that are critical to understanding the foundations of many things from algorithms to control to learning to signal processing to communication to artificial intelligence. Similarly for modular arithmetic and probability theory. EECS70 will introduce you to these and other mathematical concepts. By the end of the semester, you should have a firm grasp of the theoretical basis of these concepts and their applications to general mathematical problems. In addition, you will learn how they apply to specific, important problems in the field of EECS.
This course is divided into five main units, each of which will introduce you to a particular mathematical concept as well as its applications. The units are as follows:
These units will now be described in more detail.
Logic and Proofs
Modular Arithmetic
Counting and Discrete Probability
Continuous Probability
Diagonalization and Self-Reference
Homeworks will be assigned each Monday evening and will be due the following Monday at noon. NO late homeworks will be accepted.
Your lowest homework score of the semester will be dropped.
As a part of the homework, you will sometimes be asked to "virtual labs" that involve programming and plotting things. Knowing how to simulate and explore what actually can happen is an important skill and is very useful in learning the material and developing an intuition for it. To help students in this process, the course staff has prepared an official EECS 70 virtual machine that is running Ubuntu with the ipython and ijulia packages, as well as LaTeX, fully installed and ready for you to use. Simply download the virtual machine and set it up using software like VirtualBox for your preferred platform. The virtual machine comes preloaded with some sample code in ipython. Ask in Piazza if you are having any difficulty.
For problems that have a significant programming component, we will usually provide template/skeletons in Python that students can use. However, solutions are generally accepted in any programming language that students prefer.
Homeworks will be submitted electronically, as pdfs. Details of the online submission system are on Piazza. Homeworks may be prepared by hand, in LaTeX, or even using Microsoft Word (with equation editor --- but you're much better off learning LaTeX). If by hand, you will need to scan your work. Please see scanning instructions to scan to pdf.
Note that you will need to name your file "hwX.pdf" (e.g. "hw2.pdf") in order to submit it.We will have many readers for this class, but the primary way that the homework will be graded is by yourselves. Solutions will be posted online and then you will be expected to read them and enter your own scores and comments for every problem in the homework on a simple coarse scale (0 = didn't attempt or very very wrong, 1 = off in the wrong direction or no clear direction, 2 = half-way there, 3 = mostly right but a few things missing or wrong, 4 = 100% correct). Your grades will be due within a week of the homework deadline and if you don't enter any grades by the deadline, you are giving yourself a zero on that assignment. Note: all partial credit must be justified with a comment; without a comment, no partial credit will be allowed.
Just like we encourage you to use a study group for doing your homework, we strongly encourage you to have others help you in grading your assignments while you help grade theirs. This will also help you avoid self-favoritism.
The readers are going to grading a randomly selected subset of problems and so we will catch any attempts at trying to inflate your own scores. This will be considered cheating and is definitely not worth the risk.
There will be two midterms and one final exam.
The instructors and TA will post announcements, clarifications, hints, etc. on Piazza. Hence you must check the CS70 Piazza page frequently throughout the term. (You should already have access to the CS70 Spring 2014 forum. If you do not, please let us know.) If you have a question, your best option is to post a message there. The staff (instructors and TAs) will check the forum regularly, and if you use the forum, other students will be able to help you too. When using the forum, please avoid off-topic discussions, and please do not post answers to homework questions before the homework is due.
If your question is personal or not of interest to other students, you may mark your question as private on Piazza, so only the instructors will see it. If you wish to talk with one of us individually, you are welcome to come to our office hours. Please reserve email for the questions you can't get answered in office hours, in discussion sections, or through the forum.
In a class this large, it can be challenging for the instructors to gauge how smoothly the class is going. We always welcome any feedback on what we could be doing better. If you would like to send anonymous comments or criticisms, please feel free to use an anonymous remailer like this one to avoid revealing your identity.
We expect you to remember the math you learned in high school. Sophomore mathematical maturity (a solid understanding of the material in Math 1A, 1B), and programming experience equivalent to that gained in CS10 or the Advanced Placement Computer Science A course (e.g., CS 10, E 7, CS 61A). If you lack any of these prerequisites, you may only take the class with special permission from the instructor. Although most of the work in the class will be pencil-and-paper exercises, we expect the students to be familiar with reading and designing programs. There will be simulation and plotting exercises for you to do.
Please enroll in a discussion section via Telebears, if you have not already. You may only enroll in a discussion section that has space available: see the online schedule. Outside of your discussion section, you should feel free to attend any of the staff office hours and ask any of us for help. Unofficially, you are welcome to attend other discussion sections but only if there is physical room. Get up and leave if there are registered students waiting. Keep in mind that it will be difficult for a TA whom you see infrequently to give you a fair participation grade so regularly attending the same section(s) is encouraged.
You are encouraged to work on homework problems in study groups of two to four people; however, you must always write up the solutions on your own. Similarly, you may use books or online resources to help solve homework problems, but you must always credit all such sources in your writeup and you must never copy material verbatim. We believe that most students can distinguish between helping other students and cheating. Explaining the meaning of a question, discussing a way of approaching a solution, or collaboratively exploring how to solve a problem within your group is an interaction that we strongly encourage. But you should write your homework solution strictly by yourself so that your hands and eyes can help you internalize this material. You must explicitly acknowledge everyone whom you have worked with or who has given you any significant ideas about the homework. Not only is this good scholarly conduct, it also protects you from accusations of being a jerk or free-rider regarding your colleagues' ideas.
Warning: Your attention is drawn to the Department's Policy on Academic Dishonesty. In particular, you should be aware that copying or sharing solutions, in whole or in part, from other students in the class or any other source without acknowledgment constitutes cheating. Any student found to be cheating risks automatically failing the class and being referred to the Office of Student Conduct.
Are you struggling? We'd rather you approached us for help, rather than falling behind gradually over the semester until things become untenable. Sometimes this happens when students are afraid of an unpleasant conversation with a professor if they admit to not understanding something. We would much rather deal with your misunderstanding early than deal with its consequences later. Even if you are convinced that you are the only person in the class that doesn't understand the material, and that it is entirely your fault for having fallen behind, please overcome any feelings of guilt and ask for help as soon as you need it -- we can almost guarantee you're not the only person who feels this way. Don't hesitate to ask us for help -- we really do care that you learn!
If you have been issued a letter of accommodation from the Disabled Students Program (DSP), please contact Professor Sahai as soon as possible to work out the necessary arrangements. If you need an accommodation and have not yet seen a Disability Specialist at the DSP, please do so as soon as possible.
If you would need any assistance in the event of an emergency evacuation of the building, the DSP recommends that you make a plan for this in advance. (Contact the DSP accest specialist at 643-6456.)
If you have a fever, do not come to lecture or discussion or office hours or to the problem set party until at least 24 hours after the fever has passed. Email the head GSI (Kate -- ucb.ta.kate@gmail.com) to let her know. If this forces you to miss a homework, we will drop an extra homework for you.
Similarly, do not attend a midterm if you have a fever. Please let us know a short time in advance if this is going to happen, and we will make appropriate accomodations.
For non-contagious illnesses, use your good judgement. But spreading contagious disease is just horrible manners if you can prevent it.
The following tips are offered based on our experience with this course.
Don't fall behind! In a conceptual class such as this, it is particularly important to maintain a steady effort throughout the semester, rather than hope to cram just before homework deadlines or exams. This is because it takes time and practice for the ideas to sink in. Make sure you allocate a sufficient number of hours every week to the class, including enough time for reading and understanding the material as well as for doing assignments. (As a rough guide, you should expect to do at least one hour of reading and two hours of problem solving for each hour of lecture.) Even though this class does not have any major projects, you should plan to spend as much time on it as your other technical classes.
Do the homeworks! The homeworks are explicitly designed to help you to learn the material as you go along. Although the numerical weight of the homeworks is not huge, there is usually a strong correlation between homework scores and final grades in the class. (The most common denominator among people who do poorly in the class is that they skipped several homework assignments or multiple homework problems.)
Also, you must read the sample solutions. You may well learn a different way of looking at the problem, and you may also benefit from emulating the style of the solutions. (In science people learn a lot from emulating the approach of more experienced scientists.)
Don't wait until the last minute to start homeworks! A good practice is to read through the homework problems as soon as they are available, and let them percolate in your brain. Think through possible approaches while you are waiting in line, or stuck in an elevator, or whatever. Sleeping on a problem has often helped people to come up with a creative approach to it. Definitely do not wait until the night before it is due to start working on the homework.
Take part in discussion sections! Discussion sections are not auxiliary lectures. They are an opportunity for interactive learning. The success of a discussion section depends largely on the willingness of students to participate actively in it. As with office hours, the better prepared you are for the discussion, the more you are likely to get out of it.
Form study groups! As stated above, you are encouraged to form small groups (two to four people) to work together on homeworks and on understanding the class material on a regular basis. In addition to being fun, this can save you a lot of time by generating ideas quickly and preventing you from getting hung up on some point or other. Of course, it is your responsibility to ensure that you contribute actively to the group; passive listening will likely not help you much. And recall the caveat above that you must write up your solutions on your own. You are strongly advised you to spend some time on your own thinking about each problem before you meet with your study partners; this way, you will be in a position to compare ideas with your partners, and it will get you in practice for the exams. Make sure you work through all problems yourself. Some groups try to split up the problems ("you do Problem 1, I'll do Problem 2, then we'll swap notes"); not only is this a punishable violation of our collaboration policies, it also ensures you will learn a lot less from this course.