import numpy as np
from __future__ import division
import matplotlib.pyplot as plt
from IPython import display
%matplotlib inline
In this assignment we will explore some of the basic elements of compressed sensing: Sparsity, Incoherent measurements and the Sparsity based reconstruction.
Sparse Signal denoising¶
Before we start with compressed sensing, we’ll look at sparse signal de-noising. There’s a strong connection between compressed sensing and denoising. Here we'll attempt to denoise a sparse signal that is corrupted by random noise.
Generate a length-128 vector, x, with 5 non-zero coefficients and permute them randomly using:
x = np.array( [0.2, 0.5, 0.6, 0.8, 1] + [0] * (128-5) )
x = x[ np.random.permutation(128) - 1 ];
Plot the resulting signal using plt.stem(x)
# Your code here:
Add random gaussian noise with standard deviation $\sigma = 0.05$ to the signal, $y = x + n$ and plot it
y = x + 0.05 * np.random.randn( 128 )# Your code here:
Many approaches for denoising and regularization use the Tychonov penalty to estimate the signal from noisy data. Specifically, they try to solve:
$$\hat x = \arg\min_{x} \frac{1}{2} ||x - y||_2^2 + \frac{\lambda}{2} ||x||_2^2$$This optimization trades the norm of the solution with data consistency. The nice thing about this approach that it has a closed form solution, and finding the minimum is a linear problem.
Q) Show that the solution for this problem is
$$\hat x = \frac{1}{1+\lambda} y $$A):
Observe what happens when we plot the result for $\lambda = \{0.01, 0.05, 0.1, 0.2\}$. Use plt.stem(xhat) to plot the results.
# Plot the resulting signals (xhat) for lambda = [0.01, 0.05, 0.1, 0.2]
# Your code here:
Q) Is the solution sparse?
A)
Sparse Signals and the $\ell_1$ Norm¶
Instead of Tychonov regularization, which penalizes the $\ell_2$ norm ($||x||_2 = \sum_i |x_i|^2)$ ), we will use the an $ \ell_1$ norm ($||x_1|| = \sum_i |xi|$) penalized solution. Specifically we will solve:
$$ \hat x = \arg\min_{x} \frac{1}{2} ||x - y||_2^2 + \lambda ||x||_1 $$It turns out that this is very easy to solve. Because the variables $\hat x$'s are independent we can minimize each of them separately by solving
$$\arg\min_{x_i} \frac{1}{2}(x_i - y_i)^2 + \lambda ~|x_i|$$The solution to each $x_i$ has a closed form.
Q) Show that when $ y > \lambda$, the solution is
$$ \hat x = y - \lambda $$when $ y < -\lambda$,
$$ \hat x = y + \lambda $$and when $ -\lambda <= y <= \lambda$
$$ \hat x = 0 $$A) Derivation of soft-thresholding:
Write a function SoftThresh that accepts $y$ and $\lambda$ and returns $\hat x$. Plot the output for $t \in [-10, 10]$ and $\lambda = 2$.
def SoftThresh(y, t):
# SoftThresh -- Apply Soft Threshold to y
# Usage
# x_hat = SoftThresh(y, t)
# Output:
# x_hat = sign(y)(|y|-t)_+
# Plot the output for t in [-10, 10] and lambda = 2
# Your code here:
The effect of this function is often referred to as soft-thresholding or shrinkage. Describe what happens when $y$ is small compared to $\lambda$, and when $y$ is large.
A)
Apply SoftThresh to the noisy signal $y$ with $\lambda = \{0.01, 0.05, 0.1, 0.2\}$, and include the plot for $\lambda = 0.1$ with your report.
# Plot the resulting signals for lambda = [0.01, 0.05, 0.1, 0.2]
# Your code here:
Q) Is the solution sparse?
A)
Random Frequency Domain Sampling and Aliasing¶
As we mentioned before, there is a strong connection between compressed sensing and denoising. We'll now explore this connection and the importance of incoherent sampling.
First, let's set up the undersampled data. Compute the unitary Discrete Fourier transform of the sparse signal, $X=Fx$, where $F$ is a Fourier transform operator:
X = np.fft.fft(x);# Your code here:
In compressed sensing, we undersample the measurements. Recall that compressed sensing requires an incoherent measurement matrix. One good choice is the undersampled Fourier transform. With this choice, we are measuring a subset of the Fourier transform of our signal, $X_u = F_u x$, where $F_u$ is a Fourier transform evaluated only at a subset of frequency domain samples. This is an underdetermined system for which there are infinitely many signals that yield a consistent solution. However, we do know that the original signal is sparse, so there is hope that we will be able to reconstruct it.
Compressed sensing theory suggests random undersampling. To see why, we will look at equispaced undersampling and compare it to random undersampling. Undersample $X$ by 4 by taking 32 equispaced samples. Compute the inverse Fourier Transform, filling the missing data with zeros, and multiply by $4$ to correct for the fact that we only have $1/4$ of the samples.
Xu = np.zeros(128, dtype='complex');
Xu[::4] = X[::4]
xu = np.fft.ifft(Xu) * 4
This is the minimum $\ell_2$ norm solution (why?). Plot the real part of the result.
# Your code here:
A) Describe what you see:
Will we be able to reconstruct the original signal from this minimum-norm solution? Now undersample the data by taking 32 random samples. Compute the zero-filled inverse Fourier transform and multiply by $4$ again,
Xr = np.zeros(128, dtype='complex');
prm = np.random.permutation(128) - 1
Xr[ prm[:32] ] = X[ prm[:32] ];
xr = np.fft.ifft(Xr) * 4
Plot the real part of the signal.
# Your code here:
Q) Describe what you see. Will we be able to reconstruct the original signal from the result? How does this resemble the denoising problem?
A)
This is the important part, so say it out loud: By random undersampling, we’ve turned the ill-conditioned problem into a sparse signal denoising problem. However, the “noise” is not really noise, but incoherent aliasing that is contributed by the signal itself. Therefore, we might be able EXACTLY recover the sparse signal.
Reconstruction from Randomly Sampled Frequency Domain Data¶
Inspired by the denoising example, we will add an $\ell_1$ penalty and solve
$$ \hat x = \arg \min_x \frac{1}{2} ||F_ux - y||_2^2 + \lambda ||x||_1 $$
In this case, $\hat x$ is the estimated sparse signal, $F_u\hat x$ is the undersampled Fourier transform of the estimate, and $y$ are the observed samples of the Fourier transform (of the original sparse signal) that we have acquired. Now all the variables are coupled through the Fourier transform, and there is no closed-form solution. However, the problem is convex and so there is a global solution! We will arrive to the solution iteratively by applying soft-thresholding and constraining data consistency. Let $\hat X = F\hat x$ be the Fourier transform of $\hat x$, we will initialize $\hat X_0 = y$, and implement the following for the $i$'th iteration:
Compute the inverse Fourier transform to get an estimate of the signal, $\hat x_i = F^* \hat X_i$
Apply softthresholding on the signal $\hat x_i = \text{SoftThresh}(\hat x_i, \lambda)$ in the sparse signal domain
Compute the Fourier transform $\hat X_i = F\hat x_i$
Enforce data consistency for the measured observations in the frequency domain, that is
- if $ y[j] = 0 $, $ \hat X_{i+1}[j] = \hat X_i[j] $
- if $ y[j] \ne 0 $, $ \hat X_{i+1}[j] = y[j] $
Repeat until $||\hat x_{i+1} - \hat x_i ||_2 < \epsilon$
This is a Projection Onto Convex Sets (POCS) type algorithm. It is not a state-of-the art compressed sensing algorithm, but it is intuitive to understand: at each iteration, we alternate between enforcing data consistency and promoting sparsity.
To implement the algorithm, we store the randomly sampled Fourier data in Y,
with zeros for the non-acquired data, ie we set Y = Xr. Then, we initialize the estimate of the Fourier transform of the signal to
be Xi = Y. The core of the iteration can then be written as
xi = np.fft.ifft( Xi );
xi_st = SoftThresh(xi.real, lamb); # Enforce sparsity
Xi = np.fft.fft(xi_st);
Xi = Xi * (Y==0) + Y; # Enforce data consistency
Note that we take the real part of $x$ before soft-thresholding because we know that our signal is real.
For the general complex case, the SoftThresh function has to be modified to return $$ (|y| - \lambda)_+ \frac{y}{| y |}$$ instead. We will need this modification later when we deal with complex-valued MR images!!
Apply the algorithm (at least $100$ iterations) to the undersampled signal with $\lambda=\{0.01, 0.05, 0.1\}$. For each $\lambda$, also make a plot of error between the true $x$ and $\hat x$ as a function of the iteration number.
It is really cool to see the evolution of the intermediate result. To plot the signal at each iteration in python notebook, you can use the following commands within the for loop:
plt.clf()
plt.stem(xi.real)
plt.title( 'Iteration %d' % i )
display.clear_output(wait=True)
display.display(plt.gcf())# Initialize Y and Xi
# Your code here:
# Initialize lamb and niter
# Your code here:
# Loop
# Your code here:
Now, repeat the iterative reconstruction for the equispaced undersampled signal by initializing Y = Xu What’s wrong?
# Initialize Y and Xi
# Your code here:
# Initialize lamb and niter
# Your code here:
# Loop
# Your code here:
A) What's wrong?
Beyond Nyquist Rate: the Phase Transition Curve¶
We've seen that with the combination of sparsity, incoherent measurements and a sparsity based reconstruction, compressed sensing can exactly reconstruct a $5$-sparse signal with $4 \times$ undersampling. But how well does compressed sensing work with other sparsity level and undersampling factor? For bandlimited signals, we have the Nyquist rate guiding our sampling strategy. For compressed sensing we will instead look at the phase transition diagram.
The phase transition diagram is a 2D color plot that can characterize signal recovery performance. On its horizontal axis we have the undersampling factor $\delta = $( Number of measurements $n$ / Signal length $N$), and its vertical axis, we have the sparsity level $\rho = $( Number of nonzeros $k$/ Number of measurements $n$). At each point on the 2D plot, we assign the probability of exactly recovering the signal as its value (with a probability of 1 being what we want), so the resulting plot is a color plot.
In general, there will be a transition between a success region on the bottom right to a failure region on the top left in the phase transition diagram. This is because given the same number of measurements, more nonzeros in your signal will also make the recovery harder. Similarly, given the same sparsity level, less measurements will make the recovery harder.
For compressed sensing, it turns out there is a very sharp transition between success and failure in the phase transition diagram. Below the phase transition curve, we recover the signal exactly with probability almost 1. Above the phase transition curve, we can recover the signal exactly with probability almost 0. This transition curve essentially generalizes the Nyquist rate. Instead of depending on the signal bandwidth, our sampling rate now depends on the sparsity level.
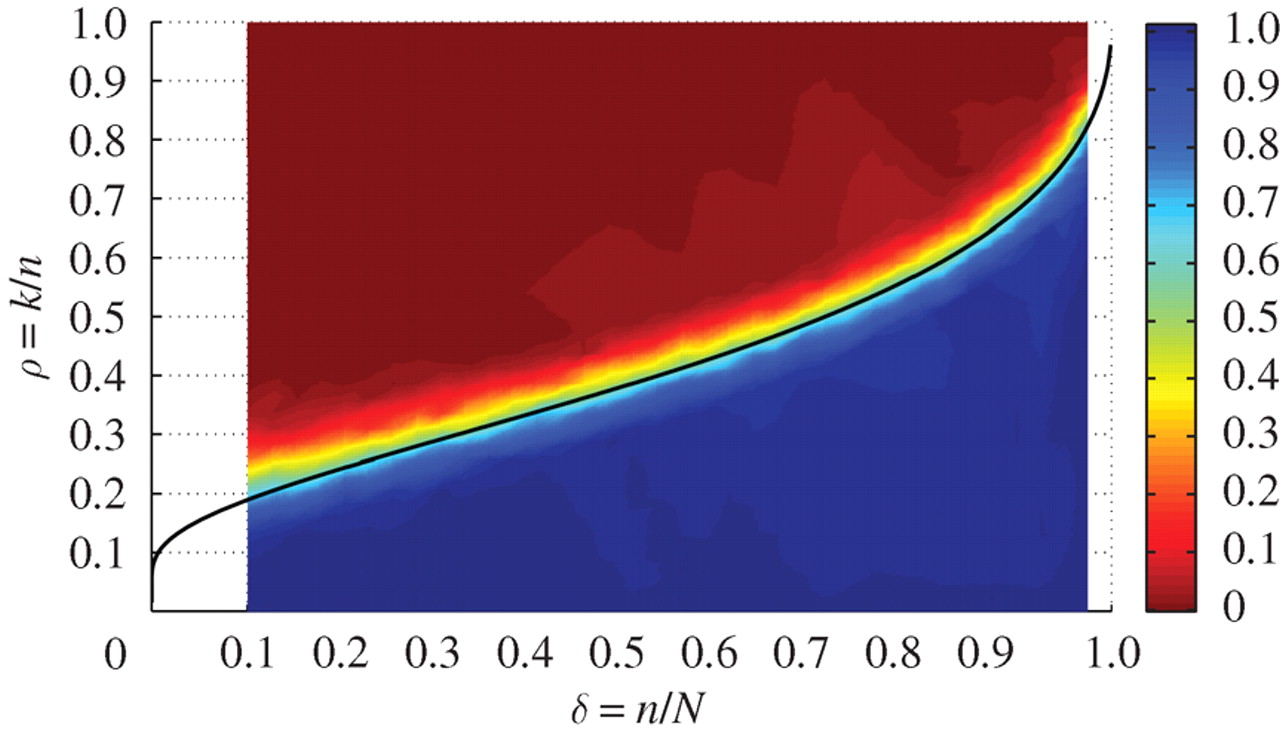
The above figure shows a compressed sensing phase transition diagram from random Fourier measurements. This figure is taken from the paper Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing by Donoho and Tanner. For each point on the diagram, the authors generate 200 random instances of the compressed sensing problem and then calculate the frequency of success as the success rate. From the diagram, we can clearly see the phase transition curve, splitting the diagram into a success region and a failure region. The phase transition curve is theoretically justified, but the details are beyond the scope of the course.
In the following part, we will empirically generate a simple version of the phase transition diagram. Instead of generating $200$ instances and assigning the probability of success, for each point in the diagram, we will assign the normalized mean square error between the recovered signal and the original signal for $8$ compressed sensing problem instances. We will consider a length $128$ signal and a $32 \times 32$ discretized phase transition diagram. For each $\delta$ and $\rho$, we will do the following four steps:
- Randomly generate a sparse vector according to $\rho$
- Take random measurements in the Fourier domain according to $\delta$
- Reconstruct the signal using the iterative reconstruction algorithm
- Compute the normalized error with the original sparse vector.
For convenience, first create a function x_rec = cs_recon( Y, lamb, niter) that takes in the randomly subsampled Fourier measurements Y, the threshold lamb and the number of iterations niter and returns the iteratively reconstructed signal x_i
# Compressed sensing reconstruction function
def cs_recon( Y, lamb, niter ):
# Your code here:
Next, initialize the phase transition matrix as a $32 \times 32$ zero matrix. We will consider a scaled version of $\delta$ and $\rho$ by $N=128$ and loop through $32$ steps from $0$ to $127$. For each $\delta$ and $\rho$, you should generate a randomly signed $k$-sparse vector with $k = \rho \delta / 128$:
# Generate signal and spectrum
k = np.floor(rho * delta / 128)
x_orig = np.append( np.sign(np.random.randn(k)) , np.zeros( (1,128-k) ) )
x_orig = x_orig[ np.random.permutation(128) - 1 ];
X_orig = np.fft.fft(x_orig)
Then generate a randomly undersampled spectrum $Y$ with $\delta$ number of measurements and reconstruct it just as we did in the first part of the exercise. Use $\lambda = 0.05$ and $30$ iterations. After reconstruction, add the normalized mean squared error to each point of the phase transition diagram:
phase_transition[rho / 4, delta / 4] += np.linalg.norm( x_rec - x_orig ) / (np.linalg.norm( x_orig ) + 1e-5)
Do the above steps $8$ times and divide the resulting phase_transition by $8$. Your resulting code should have 3 for loops.
Generate the phase transition matrix and plot it using plt.imshow(). Note that it may take a while to generate the matrix. If you are impatient, you can put a print statement after the first for loop.
# Initialize phase transition matrix
# Initialize lamb and niter
# Your Code Here:
# Loop through iterations
# Loop delta and rho from 1 to 127 in 32 steps
# 1. Generate signal and spectrum
# 2. Random undersample
# 3. Reconstruct
# 4. Compute normalized error
# Your Code Here:
print "done"
# Plot phase transition matrix
plt.figure(figsize=(6, 6))
plt.imshow(phase_transition[1:-1,1:-1], origin='lower', extent = (0.03125, 1-0.03125, 0.03125, 1-0.03125), vmax = 0.4)
plt.colorbar()
plt.title( 'Phase Transition' )
plt.xlabel('Measurements (n) / Signal length (N)')
plt.ylabel('Sparsity (k) / Measurements (n)');
Q) Do you see a phase transition? Is it as precise as the paper figure? Why and why not? Does it match your expectation?
A)
Note that because we are only doing one problem instance at a single point, this is a very coarse version of the phase transition curve. Luckily we have ~50 people in the class. Each person will generate a different random instance, and by averaging, we can get a more accurate phase transition diagram.
Save the phase transition matrix with np.save() and submit it along this python notebook. After collecting all the reports, we will average the matrices from everyone and hopefully get a more precise phase transition diagram!
#np.save('phase_transition',phase_transition)
Medical Image Sparsity¶
Even without noise, medical images are generally not sparse. However, like natural images, medical images have a sparse representation in a transform domain, such as the wavelet domain. Here we will use the PyWavelets package to perform wavelet transforms. You can install the package with the command
pip install PyWaveletimport pywt
plt.rcParams['figure.figsize'] = (16, 16)
The PyWavelet package does not provide nice functions for visualizing the wavelet transforms. To do this, we need to define functions that stack and unstack the approximation and detail coefficients, as well as scale the different levels when displaying an image. We provide you this functionality with the code below
def imshowgray(im, vmin=None, vmax=None):
plt.imshow(im, cmap=plt.get_cmap('gray'), vmin=vmin, vmax=vmax)
def wavMask(dims, scale):
sx, sy = dims
res = np.ones(dims)
NM = np.round(np.log2(dims))
for n in range(int(np.min(NM)-scale+2)//2):
res[:int(np.round(2**(NM[0]-n))), :int(np.round(2**(NM[1]-n)))] = \
res[:int(np.round(2**(NM[0]-n))), :int(np.round(2**(NM[1]-n)))]/2
return res
def imshowWAV(Wim, scale=1):
plt.imshow(np.abs(Wim)*wavMask(Wim.shape, scale), cmap = plt.get_cmap('gray'))
def coeffs2img(LL, coeffs):
LH, HL, HH = coeffs
return np.vstack((np.hstack((LL, LH)), np.hstack((HL, HH))))
def unstack_coeffs(Wim):
L1, L2 = np.hsplit(Wim, 2)
LL, HL = np.vsplit(L1, 2)
LH, HH = np.vsplit(L2, 2)
return LL, [LH, HL, HH]
def img2coeffs(Wim, levels=4):
LL, c = unstack_coeffs(Wim)
coeffs = [c]
for i in range(levels-1):
LL, c = unstack_coeffs(LL)
coeffs.insert(0,c)
coeffs.insert(0, LL)
return coeffs
def dwt2(im):
coeffs = pywt.wavedec2(im, wavelet='db4', mode='per', level=4)
Wim, rest = coeffs[0], coeffs[1:]
for levels in rest:
Wim = coeffs2img(Wim, levels)
return Wim
def idwt2(Wim):
coeffs = img2coeffs(Wim, levels=4)
return pywt.waverec2(coeffs, wavelet='db4', mode='per')
Before we dive into wavelet transforms, we need a nice image to perform the tests. The provided brain.npz file from the webpage has a very pretty brain image (note it is complex-valued!). Run the cell below to load this and other data, explained later.
data = np.load('brain.npz')
im, mask_unif, mask_vardens, pdf_unif, pdf_vardens = \
data['im'], data['mask_unif'], data['mask_vardens'], data['pdf_unif'], data['pdf_vardens'],
Here's an example of how to compute a Daubechies wavelet transform, display it, and reconstruct it again:
Wim = dwt2(im)
im2 = idwt2(Wim)
plt.subplot(1,3,1)
imshowgray(np.abs(im))
plt.title('Original')
plt.subplot(1,3,2)
imshowWAV(Wim)
plt.title('DWT')
plt.subplot(1,3,3)
imshowgray(np.abs(im2))
plt.title('Reconstruction')
print 'Reconstruction error:', np.linalg.norm(im - im2)
We will now evaluate the sparse approximation of the brain image. Wavelet coefficients represent both space and spatial frequency information. Each band of wavelet coefficients represents a scale (frequency band) of the image. The location of the wavelet coefficient within the band represents its location in space. What you see are edges of the image at different resolutions and directions. Threshold the wavelet coefficients retaining only the largest 20% of the coeffi- cients. You can threshold im W for the largest fraction f of the coefficients with
m = np.sort(abs(Wim.ravel()))[::-1]
ndx = int(len(m) * f)
thr = m[ndx]
Wim_thr = Wim * (abs(Wim) > thr)
Plot the masked wavelet coefficients. What has been thresholded?
## Code to threshold and display the wavelet coefficients
Reconstruct the image and display it. Compare it to the original image qualitatively and by computing the difference image. What has been removed? Examine the results when you retain the largest 12.5%, 10%, 5% and 2.5% of the coefficients. What, in your opinion, is the sparsity level of the image? Provide a reconstruction and difference image to support your argument.
## Your code here
Your Explanation:
Compressed Sensing MRI¶
We'll now explore 2D compressed sensing reconstruction from under-sampled data. The brain.npz file contains additional data, which we have already loaded
Non-uniform random sampling¶
An important aspect of random frequency-domain sampling is matching the power spectrum of the image. Since the energy in many images is concentrated in lower spatial frequnecies, more samples should be allocated there. We have provided two 3-fold undersam-pling masks for you. The random masks are in the variables mask_unif and mask_vardens and were drawn from probability density functions (PDF) given by the variables pdf_unif and pdf_vardens, respectively.
Compute the 2D Fourier transform of the image using a centered 2D FFT. Multiply by the uniform mask, divide by the appropriate PDF (called density compensation), and compute the zero-filled Fourier transform:
M = fft2c(im);
Mu = (M * mask_unif) / pdf_unif;
imu = ifft2c(Mu);
Display the image and the difference image compared to original image. Is the aliasing white random noise? Repeat for the variable density mask. What happened now? Both use a similar number of samples, but which gives you a better reconstruction?
def fft2c(x):
return 1 / np.sqrt(np.prod(x.shape)) * np.fft.fftshift(np.fft.fft2(np.fft.ifftshift(x)))
def ifft2c(y):
return np.sqrt(np.prod(y.shape)) * np.fft.ifftshift(np.fft.ifft2(np.fft.fftshift(y)))
## Your code here
Your Explanation:
Reconstruction from Random Sampled k-Space Data¶
Extend your 1D POCS algorithm for 2D images. Add another step of computing the wavelet transform before the soft-thresholding and the inverse wavelet transform after the soft-thresholding. Make sure that your SoftThresh function works for complex-valued data, as was mentioned earlier.
Reconstruct the images from both the uniform and the variable density under-sampled data. First get an idea of reasonable values for $\lambda$ by examining what would be thresholded. You can do this using
Wimu = dwt2(imu)
imshowgray(abs(Wimu) > lambda)
Don't use imshowWAV for this, since it will scale the different wavelet levels differently. You want a significant number of coefficients to be below $\lambda$, but not so many that too much detail will be lost!
Start with the variable density data, and experiment with several values of $\lambda$. You should only need about 20 iterations, but start with fewer while you convince yourself it is working! Compare the result after soft-thresholding to a zero-filled density compensated reconstruction, the original image, and a the original image soft-thresholded. As an initial image to the POCS, use a zero-filled density compensated reconstruction, as it will converge faster. Show the image, and the difference image for the $\lambda$ you find the most effective.
Then try the uniform density data. Run for at least 50-100 iterations, since this converges slowly. If you want to speed up the convergence, start with a relatively large $\lambda$ so that the recon will converge rapidly. Then, decrease $\lambda$ using the previous recon as an initial image. For example, you might divide $\lambda$ by two every 10 or 20 iterations (this is called continuation). Show the image, and the difference image for the $\lambda$ (or the final $\lambda$ if you use a sequence) that you find the most effective. Don’t spend too much time on this, the point should be clear by now.