Homework Assignment 10 Solutions
1) We must first introduce feedback variables around which to organize
the analysis of this asynchronous feedback circuit. Drawn in Figure 1 is
one such choice of feedback variables. The buffers represent delays in
commiting new values for the feedback variables (Pi where i
e {1, 2, 3}) to the feedback variable (Qi
where i e {1, 2, 3}).
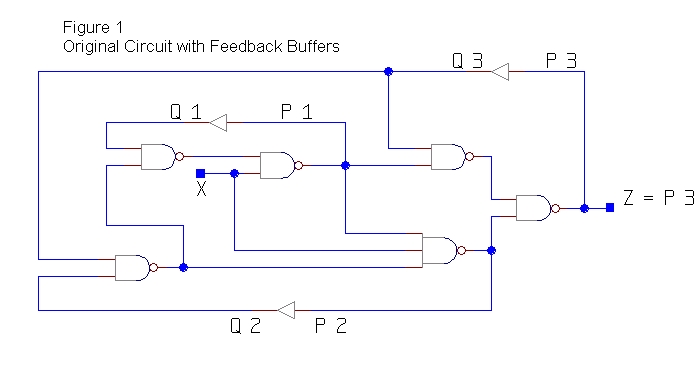
We may now think of the circuit
as a combinational logic taking as inputs the Qi and X
and generating outputs Pi and Z, where the outputs Pi
are fed back into the combinational logic after a delay to the inputs Qi
(much like our picture of a synchronous sequential logic but with delay
buffers in place of flip-flops). The combinational circuit at the core
of the system's behavior may then be drawn as in Figure 2.
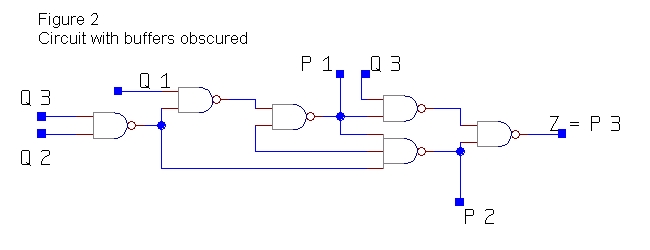
We may now immediately extract from
the above circuit the following minterm equations:
P1 = ((Q2
nand Q3) nand Q1)
nand X = ( (not Q3)*
Q2) + ((not Q2)
* Q1) + (not X))
P2 = not(X * P1
* ( Q3 nand Q2))
=
(not X) + (X*(not Q1)
+ (X*Q2*Q3)
+ (X*(not Q1)*Q3)
+ (X*(not Q1)*Q2)
+ (Q2*Q3)
Z= P3=not(P2*(not
(P1*Q3)))
= ( (not Q2)*Q1*Q3)
+ ( (not X)*Q3) +
(X*Q1*(not Q2)*(not
Q3))
The Karnaugh Maps are then as follows,
where the bold and italicized cells represent stable total states:
Karnaugh map for P1
|
XQ1
Q2Q3
|
00
|
01
|
11
|
10
|
|
00
|
1
|
1
|
1
|
0
|
|
01
|
1
|
1
|
1
|
0
|
|
11
|
1
|
1
|
0
|
0
|
|
10
|
1
|
1
|
1
|
0
|
Karnaugh map for P2
|
XQ1
Q2Q3
|
00
|
01
|
11
|
10
|
|
00
|
1
|
1
|
0
|
1
|
|
01
|
1
|
1
|
0
|
1
|
|
11
|
1
|
1
|
1
|
1
|
|
10
|
1
|
1
|
0
|
1
|
Karnaugh map for P3=Z
|
XQ1
Q2Q3
|
00
|
01
|
11
|
10
|
|
00
|
0
|
0
|
1
|
0
|
|
01
|
1
|
1
|
1
|
0
|
|
11
|
1
|
1
|
0
|
0
|
|
10
|
0
|
0
|
1
|
0 |
This makes the computation of the state
and output sequences corresponding to a given input sequence rather transparent
Flow table starting with the unique stable X=0
and Z=0 total state(bold and italics means stable).
|
Q1Q2Q3
|
X
|
|
0
|
1
|
|
110
|
110;0
|
101;1
|
|
101
|
111;1
|
101;1
|
|
111
|
111;1
|
010;0
|
|
010
|
110;0
|
010;0
|
So, starting with stable X=0 and Z=0
and subsequently <X>=<0, 1, 0, 1, ...> (with transitions in X consistent
with the fundamental mode assumption), we get the following sequence (ignoring
any race conditions) for internal state and output:
<Q1Q2Q3Z>
= < 1100, 1000, 1011, 1111, 0100 ...>
where the ellipsis here means we
henceforth see repetitions of the sequence seen so far repeated.
b) For Q1Q2Q3=111
and X=0, a transition of X to 1 makes, supposedly,
Q1Q2Q3 go from 111 ->
010. This is a two variable transition. Under the fundamental mode assumption,
we will actually first see either
Q1Q2Q3: 111 ->
110 or Q1Q2Q3:
111 -> 011. We
furthermore cannot say which of these transitions will occur, as this
is determined (if it is deterministic) by the technology dependent timing
of the circuit. Looking at the Karnaugh maps, we see that the internal
state will subsequently stabilize at 100 or 010, as X:0->1
causes either
Q1Q2Q3: 111 ->
110 ->100 or
Q1Q2Q3: 111 ->
011 ->010.
This is therefore a critical race, as, we have shown, $
an input sequence such that $
two distinct sequences of resulting
stable states. The behavior of this asynchronous state machine is therefore
left undetermined.
2a) First pass at Compatibility diagram,
where X means the states are ostensibly incompatible (which is to
say the outputs are different) and Y that the states are ostensibly compatible
(which is to say outputs and next states are identical):
|
2
|
6~4 5~3
|
|
3
|
X
|
X
|
|
4
|
X
|
X
|
Y
|
|
5
|
Y
|
6~4 5~3
|
X
|
X
|
|
6
|
Y
|
6~4 5~3
|
X
|
X
|
Y
|
|
7
|
X
|
X
|
6~4 5~3
|
6~4 5~3
|
X
|
X
|
|
8
|
X
|
X
|
5~3
|
5~3
|
X
|
X
|
6~4
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
As there is an "X" in cell (3, 5) and there is an "X" in cell (4, 6),
the next pass completes the reduction:
|
2
|
X
|
|
3
|
X
|
X
|
|
4
|
X
|
X
|
Y
|
|
5
|
Y
|
X
|
X
|
X
|
|
6
|
Y
|
X
|
X
|
X
|
Y
|
|
7
|
X
|
X
|
X
|
X
|
X
|
X
|
|
8
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
So the compatibilities are 1~5~6, 3~4. The reduced table is therefore
|
X1X2
|
Z
|
|
00
|
01
|
11
|
10
|
|
1
|
6
|
5
|
2
|
0
|
|
1
|
4
|
3
|
2
|
0
|
|
8
|
4
|
3
|
7
|
1
|
|
8
|
6
|
5
|
7
|
1
|
|
8
|
4
|
5
|
7
|
1
|
c) This one is pretty straight forward:
Merged Flow Table
|
Q1Q2
|
AB
|
|
00
|
01
|
11
|
10
|
|
00
|
1
|
7
|
8
|
2
|
|
11
|
3
|
5
|
6
|
4
|
|
01
|
3
|
7
|
8
|
2
|
|
10
|
3
|
7
|
6
|
4
|
Glitch-free output assignment
|
AB
|
|
00
|
01
|
11
|
10
|
|
1
|
0
|
-
|
1
|
|
0
|
1
|
-
|
-
|
|
-
|
-
|
1
|
1
|
|
0
|
-
|
0
|
1
|