CS152 Computer Architecture and Engineering

Homework 1 is due at the start of the lab section on Friday, 3/4. Please include your NAME, STUDENT ID and LOGIN on your homework.

Homework Policy:

• No late homeworks will be accepted.

• You may discuss problems with your friends, but all work must be done individually and you must be able to prove that you understand everything that you hand in.

• If we can't read it from 2 feet away, we won't grade it.

Problem 1

Consider a CPU that only executes the R-format ALU instructions in the MIPS-II subset used in Lab 2:

addu, subu, sll, srl, slt

Note that because these are R-format instructions, there is no immediate field to hold a constant value. In this problem, asssume the values of R1-R31 are randomly initialized, and may hold any of the 2^32 integer values, including 0. Ignore the fact that it may be possible to prove that certain values could never appear in certain registers, because the registers serve as stack pointers, frame pointers, etc. R0 holds the value 0 as expected.

We wish to write a program using only these instructions, that upon completion results in R1 holding the constant 1, R2 holding the constant 2, R3 holding the constant 3, and R4 holding the constant 4 (all constants above expressed in decimal).

1. Is it possible to write this program using the 5 instructions listed above?
2. Looking at Appendix A's description of the MIPS II instruction set, choose the smallest set of R-format ALU machine instructions (NOT pseudoinstructions) that are needed to write this program (there may be many equally-small subsets of instructions: any one will do). Which instruction(s) did you choose?
3. Write the main body of this program (no need to write the entry and exit code -- just a straight-line sequence of instruction that computes the values of R1, R2, R3, R4).

Problem 2

In MIPS, instructions are constrained to be word-aligned. An attempt to execute an instruction on a non-aligned boundary must result in an exception that ends the program (to simplify the Labs, we do not require that you support this semantics, but for this problem, we consider it to be a part of the programmers contract).

Assume you are designing a CPU for the instruction subset supported in Lab 3. To simplify the CPU, a team member suggests that the machine be built with a 30-bit Program Counter. He claims that the branch arithmetic datapath surrounding the PC can remain unchanged: each 32-bit datapath element can be converted into a 30-bit datapath element, simply by removing the lower 2 bits of logic.

1. Is his claim correct? If it is not, show a machine code snippet (using only the Lab 3 instructions) whose correct semantics would be impossible to get right with the proposed changed.
2. Is it possible to add a small amount of logic to this 30-bit datapath to solve the problem? Or is the team member's idea unworkable? If it is possible, show a high-level block diagram of the PC-update datapath with the fix.

Problem 3

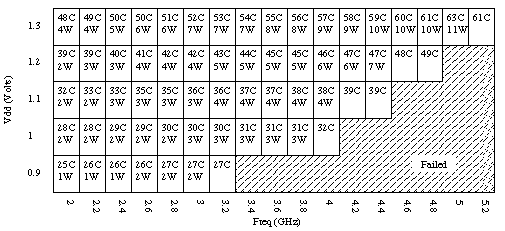
The table below shows the "Schmoo plot" for one Synergistic Processing Unit of the new IBM/Sony/Toshiba cell processor. A Schmoo plot shows, for a given power supply voltage, how fast the processor can be clocked. This Schmoo plot also shows the die temperature and power consumption for each pair.

Assume that for the Cell processor, clock frequency is proportional to performance (thus, a processor clocked at 4 GHz will execute a program twice as fast as one clocked at 2 GHz). Also assume that it is (for example) possible to break up a program running on 1 4 GHz Cell processor to run on 2 2 GHz Cell processors, so that the two-processor system executes the program as quickly as the one-processor system.

Notice that at 1.3 V, a single processor can run at 4.8 GHz, while consuming 10 W.

1. Given the assumptions above, what is the smallest number of Watts attainable by using 2 processors to get 4.8 GHz performance? List the Vdd and clock speed needed for each processor.
2. Part A shows that parallelism is an effective way to reduce power for the same performance, if the voltage is scaled. Give an intuitive explanation of why this power-saving "trick" works.
3. For the 2.2 Ghz frequency, make a "theory vs practice" plot that compares the voltage dependence on power with the theoretical switching-power equation described in the 2/8 lecture. This plot should have 5 data points, one for each Schmoo plot entry for 2.2 GHz. To make this plot, normalize the theory plot so that it has the same power as the data for Vdd = 0.9V (show the normalization math in your answer). Does theory overestimate or underestimate the actual power?

   ---