Description:

Here we describe the Earley parsing algorithm. We will work through two examples and write out pseudocode to help us understand the algorithm. We we finally consider some more advanced issues. All of this will help with the PA5 ssignment, where you have to understand and extend an Earley parser.
To help us understand how Earley works, let us work through some examples. First, let us consider the following grammar.
| E | ::= | T + id | id |
| T | ::= | E |
id + id + id
We will generate the following sequence of steps (with Graphviz doing some strange layouts, but hey, I bet you couldn't do that well in under a second):
First
Prev
Next
Last
Description:

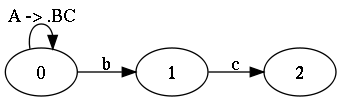
For another example, consider the following grammar.
| A | ::= | BC |
| B | ::= | b |
| C | ::= | c |
bc
We will generate the following sequence of steps.
First
Prev
Next
Last
Description:
How do we know whether we accept the final string? We want to do so if there is some derivation from the start non-terminal that consumes the entire string. This is represented in our graph by an edge from the beginning of the input string to the end that is labeled by a completed production of the start non-terminal. The edge we added at step ten of the first example and the edge we added in the final step of the second example are such edges.
So far our algorithm only accepts or rejects strings. How can we build the parse tree from the result of this algorithm? The answer lies in working backward from the final edge, just as in CYK. In the first example, we added the final edge labeled by "E -> T+id." from the edge "T -> E." that goes to node 3 and the final two "+" and "id" tokens, so those are the node's three children. We then similarly work backwards from this "T -> E." edge. The Earley algorithm adds each edge because of some other edge, so we can go backward to determine the exact parse tree.
In the course of our examples, you may have noticed that some of the edges are different from others. Specifically, consider which edges we might use when working backward to build the parse tree. We only want to add nodes in the parse tree corresponding to edges representing "completing" a production. These edges, which are labeled with a "." at the end of the production, are called completion edges. For other edges we we consume a token of the input and move one terminal forward in the labeling production. These edges, with a dot before a terminal, are called scanning edges. Finally, some edges tell us that we are expecting a non-terminal, so we add edges representing that non-terminal's productions. These edges, with a dot before a non-terminal, are called prediction edges. These are the three different types of edges in the Earley algorithm.
Let us now write some pseudocode for the algorithm to help us better understand it. First, consider how the algorithm works. We initially added one edge for each of the start non-terminal's productions. We then added new edges because of the existing edges (using prediction and completion; see below) and then continued left-to-right across the input until the entire input was processed. So the Earley algorithm maintain a list of edges. In each step, it predicts and completes edges until no more edges can be added; it then scans the input, consuming the next input token. Thus the main part of the Earley algorithm lies in describing how it handles the three types of edges.
First, let us decide how to represent an edge. Each edge has a start location, an end location, and a label. The two locations are integers, and the third we will represent in our pseudocode with the production itself (consider it a string, if you wish). Note that here, as always, capital letters stand for non-terminals and lowercase letters stand for terminals. We will additionally use Greek characters (α, β, γ, and δ) to represent arbitrary parts of a production.
We can now write some pseudocode for the three types of edges. Scanning edges are the simplest.
def scanning(i, j, A -> α.bβ):
if input_str[j] == b:
enqueue(i, j+1, A -> αb.β)
def prediction(i, j, A -> α.Bβ):
for each production of the form B -> γ
enqueue(j, j, B -> .γ)
def completion(i, j, A -> α.):
for each existing edge of the form (k, i, C -> γ.Aδ)
enqueue(k, j, C -> γA.δ)
If you do not completely understand how these three edges work, try looking back through the two examples and work through them with the pseudocode in mind. This pseudocode is very similar to the Earley parser we give you in project two: look at it if you want to see how the whole parser works. Note that as mentioned above, completion edges are the only ones that correspond to building the parse tree at the end of the algorithm. The other two types of edges only help in building up the graph.
Finally, let us consider how Earley handles precedence. Consider the following (familiar) grammar.
| E | ::= | n |
| | | E+E %dprec 2 | |
| | | E*E %dprec 1 |
n+n*n
The following image shows all of the completed edges at the end of the Earley algorithm (as only the completed edges matter for reconstructing the parse tree).
This gives us a rule for precedence. But what about associativity? Consider the following simple grammar.
| %left | - | |
| E | ::= | n |
| | | E-E |
1-2-3
The Earley edges for this grammar and input are very similar to the example just above, so we will not redraw them. This string has two parse trees, and they give two different answers. Which is correct? Subtraction associates to the left, which we noted with a %left directive in the grammar. We thus want as much of the work as possible to be in the left child of the root node. So Earley can choose the edge with the largest left child.Hopefully you understand Earley better now. Isn't it fun?