In Project 1, you studied how to change the page replacement policy of the PostgreSQL buffer manager. In this project you will move to a higher level in the system and add functionality to the PostgreSQL executor. This project will be considerably more complex than Project 1, both in terms of the amount of coding involved and in understanding existing code. The major parts of the project are:
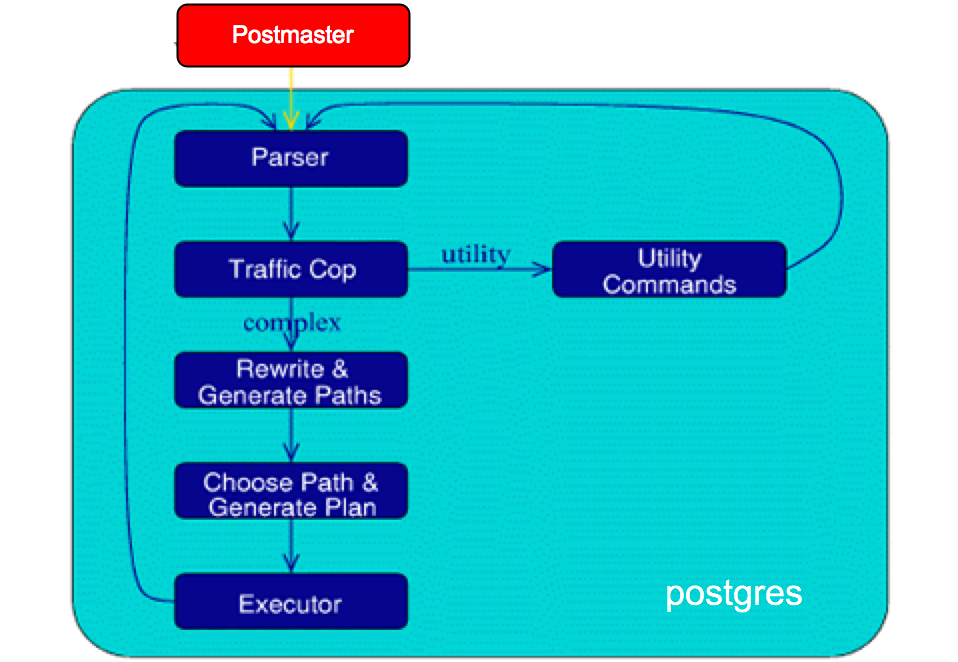
PostgreSQL Backend Flowchart

Before diving into the executor, it is useful to understand the
"life of a query" in PostgreSQL. Recall that every client
application (e.g. psql, pgaccess, or a web-server running a PHP
script) first connects over a network or a local UNIX socket to
the postmaster process, which assigns a postgres
"backend process" to that client. Subsequent interaction is done
between the client and its associated backend process.
When an SQL command string is received by the postgres backend, it is
passed to the parser which identifies
the query type, and loads the proper query-specific data
structure, like CreateStmt or SelectStmt.
The statement is
then identified as complex (SELECT / INSERT / UPDATE / DELETE --
basically the DML sublanguage of SQL) of as simple, e.g various
DDL and utility commands like CREATE USER, ANALYZE, etc. The
utility commands are processed by special-case functions in
backend/commands. Complex statements are more interesting for our
purposes in this assignment, since they eventually have to be
passed down to the executor for processing. For more details on
how a query is processed you can look
at http://www.postgresql.org/developer/ext.backend.html.
By the time a query is passed to the Postgres executor, it has been converted into a data structure consisting of a tree of plan nodes. Each node is a single query processing operator (join, disk scan, sort, etc) that consumes relations and produces relations. As described in class, PostgreSQL uses an "iterator" model to draw tuples upward from the leaves of the tree (disk scans) up to the root. To get a row, a node “pulls” on its child node, which in turns pulls on its child nodes as needed. Note that each node must ``save'' it's state to generate the tuples in an incremental on-demand fashion. To produce a result set, the main code of the executor pulls on the root node of the plan tree.
As a concrete example, consider the following single-table SQL query:
A plan tree for the above query looks like:

Note, the text in red are executor nodes that you can find in src/backend/executor/.
Approximate Query Answering using Samples: An Introduction
Data volumes are growing in modern database and "data warehouse" systems, and query-workloads are growing more complex. For many complex queries it can be almost impossible to support fast, interactive query-response times for users: conventional query-processing engines can take hours or even days in order to compute the exact answer for a very complex SQL query over Terabytes of disk-resident relational data. For several application scenarios, however, exact query answers are not really required, and, in fact, users would be much happier with a fast, approximate answer to their query (along, perhaps, with some error guarantees for the quality of the approximation). For instance, in exploratory data-analysis sessions, a user may pose aggregation queries in order to quickly discover “interesting” regions of the database or validate a hypothesis on the underlying data – clearly, in such cases, the full precision of the exact answer is not needed, and the user would actually prefer a fast, accurate estimate of the first few digits of precision for the aggregate (e.g., the leading few digits of a total in the millions or the nearest percentile of a percentage).
One reasonable way of enabling such fast, approximate query answers is to have the executor fetch a random sample of a table rather than all the tuples in the table; this feature is supported in the DB2 and Oracle database systems. Typically, each of the table’s data units (also known as sampling units) are selected for inclusion in the query processing with some probability p that is specified in the query. The sampling rate, p, specifies the size of the sample to be approximately 1/p times the size of the original table. (As we will see later, our “sampling units” can be either tuples or disk pages, giving rise to tuple-level sampling and page-level sampling schemes.) For instance, sampling at a rate of p=0.01 (or, 1%) would reduce the data volume by a factor of 100 – clearly, running our SQL query using the sample (instead of all tuples in the table) would result in far shorter response times. Several research studies have demonstrated that concise random samples of a table R can be used to accurately estimate several aggregate queries (such as AVG, SUM, and COUNT) over the attributes of R (and, at the same time, provide approximation-error guarantees based on classical statistical-sampling theory -- a detail we will not pursue in this homework).
For this homework, we will be adding support for random-sampling operators to PostgreSQL. Following the SQL 2003 standard, we will indicate sampling within an SQL query using the TABLESAMPLE clause, which can be added to each table specification in the FROM clause of an SQL statement. The TABLESAMPLE clause includes two parameters:
The optional REPEATABLE(seed) clause above is used to fix the (positive INTEGER) seed value for the random-number generator used during the sampling process. Thus, using the same seed value through a REPEATABLE clause allows users to consistently generate the same result sample sets across different runs of the SQL statement. Such repeatable results are often important when testing or debugging an implementation, or in any situation where multiple runs of the same query are desired.
We now turn to the sampling-method specifics:
When estimating aggregates using a TABLESAMPLE clause, note that, while AVG aggregates can be estimated directly over the sample, the results of COUNT and SUM functions will need to be scaled by the sampling rate in order to produce a correct estimate for the whole table. For instance, running a SUM aggregate over a 20% sample (sampling rate p=0.2) will only sum values across about 20% of the tuples; to produce a correct estimate for the full table, the sample SUM must be multiplied by 1/p=5. In general, any COUNT or SUM aggregate estimated over a sample must be divided by the sampling rate to scale the result to the full data set.
The time to execute the following query (similar to the previous one, except that it finds out the committee names as well) is an order of magnitude faster than running it against the entire data set. The following chart illustrates the results (converted to % donations) returned from the query run against the entire database, and then using one percent and ten percent sampling:
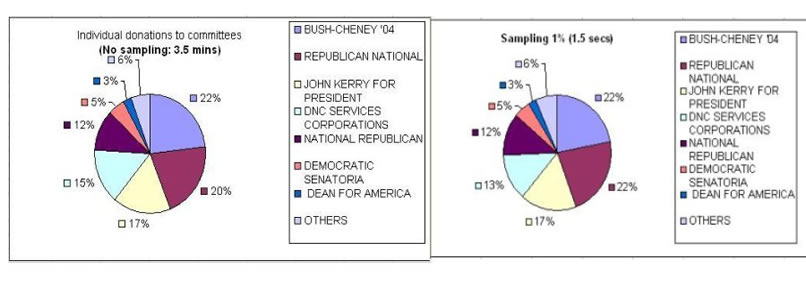 .
.
As an aside, when dealing with SQL statements over multiple tables, it is conceptually easier to use the TABLESAMPLE clause over only one of the tables in the query. Specifying sampling clauses over more than one table introduces subtle and non-trivial statistical-estimation issues (especially, when join operations are involved) that we will not try to address here.
In addition to generating random samples from tables “on-the-fly” during query processing, the TABLESAMPLE clause can also be used to pre-compute and store sample tuples as tables in the database (reflecting a concise summary or demographics of the full data). Such sample tables can be directly used for fast approximate query processing, e.g., allowing data analysts and developers to quickly test their hypotheses or code logic without having to scan large data tables in their entirety. The following SQL statement will populate a sample table with a 5% BERNOULLI sample of the original “TRANSACTIONS” table:
Setup:
Cleanup all data and src from your previous homeworks. You are going to need all the space you can free up. To find how much disk space you are using, type the following on command prompt: "du -hs $HOME". To setup for the subsequent parts, use the following:Project Part 1(a): (20%)
For part 1(a), you have to implement BERNOULLI sampling in postgres. As described earlier, BERNOULLI sampling examines each row and flips a coin (generates a random number) that determines whether the row should be selected or not. To implement BERNOULLI sampling you will modify nodeSeqscan.c in the postgres executor (src/backend/executor). nodeSeqscan implements the sequential scan operator in postgres. We would like to modify it in such a way that it can do BERNOULLI sampling when requested, and a plain sequential scan otherwise.
Postgres executor recap:
As described earlier, the executor processes a tree of "plan nodes". The plan tree is essentially a demand-pull pipeline of tuple processing operations. Each node, when called, will produce the next tuple in its output sequence, or NULL if no more tuples are available. If the node is not a primitive relation-scanning node, it will have child node(s) that it calls in turn to obtain input tuples.
Every primitive relation-scanning executor node implements the following 5 basic functions:
(Note: Italicized Node stands for any node, viz Seqscan, Tidscan, Indexscan et al)
Note that the ExecNodeNext() function call of a node is invoked by its parent, and returns with a single tuple. When that call returns, it must have explicitly stored enough information ("state") in the node's iterator variables such that the next time that ExecNodeNext() call is invoked, it can resume from wherever it left off and supply the correct next tuple.
This is a sketch of the control flow for full query processing:
CreateQueryDesc() [src/backend/tcop/pquery.c]
ExecutorStart() [src/backend/executor/execMain.c] CreateExecutorState() [src/backend/executor/execUtils.c]
ExecInitNode() [src/backend/executor/nodeX.c] ExecInitNode recursively scans plan tree
ExecutorRun() [src/backend/executor/execMain.c]
Loop until no more Tuples: ExecNodeNext() [src/backend/executor/nodeX.c] recursively calls the ExecNodeNext of the child nodes
ExecutorEnd() [src/backend/executor/execMain.c] ExecEndNode() [src/backend/executor/nodeX.c] recursively releases resources FreeExecutorState() frees per-query context and child contexts
FreeQueryDesc() [src/backend/tcop/pquery.c]
Implementing Part 1(a):
We want you to modify the seqscan node to do BERNOULLI sampling as well as regular sequential scan (in absence of any sampling). As described earlier, executor nodes generate tuples on demand and they store their current iterator state to faciliate this. The sequential scan node (nodeSeqscan) uses the SeqScanState data structure to store its state. We have added 2 fields to SeqScanState: bool tablesample and struct SampleInfo. These fields are initialized in ExecInitSeqScan() and you can assume that our code will set them to have valid data (i.e sampletype = SAMPLE_BERNOULLI, if tablesample is true; sampleseed is a positive int; and samplepercent is in [1,100]).
All executor code resides in src/backend/executor/ within the postgres directory. Henceforth any reference to executor source files without explicit paths would mean that it resides in the executor directory. All paths would be relative to the postgresql-8.0.3/ directory.
Your tasks for this part are:
We have provided the GetRandom() logic to ensure uniformity in everyone's implementation of random "coin flipping". If you use any other method to generate the random numbers then you will not get the answers we expect.
Project Part 1(b):(50%)
In this part you will implement a new executor node nodeSeqBlockscan. We have provided you with all the required glue code to ensure that a SYSTEM sample will call the appropriate methods in nodeSeqBlockscan. Your task is to fill in the nodeSeqBlockScan skeleton provided to you.
What does nodeSeqBlockscan do?
As the name suggests, this node scans a relation block-by-block (i.e. page-by-page), skipping some blocks without actually fetching them from the disk. Our goal is to implement SYSTEM sampling which flips a coin for every block (instead of every row). The advantage is that if we decide to not take a block, then we don't have to read it off the disk and this saves us I/O. If we decide to take a block, then we take all its valid tuples. (Postgres sometimes leaves invalid -- e.g. deleted -- tuples on disk pages for some time; these should be ignored.)
How to implement nodeSeqBlockscan?
SeqBlockScanState stores the iterator state for nodeSeqBlockscan. We have added the following to SeqBlockScanState:
bool tablesample and SampleInfo are as described in the previous part. They are initialized for you with valid data in the ExecInitNode(). BlockSampleState is provided to keep track of the current iterator state while scanning the relation block-by-block. We have partly filled it with the following fields:
totalblocks is initialized in ExecInitNode() with the total number of blocks in the relation.
Your task for this part is:
We provide you with a few utility functions that might be helpful to you (these functions bundle the buffer manager functions exposing a relatively simpler interface to you):
Compiling and debugging:
We recommend you to compile your code as follows (we have enabled the following by default, --enable-debug, --enable-cassert, --prefix=/home/tmp/$USER/pgsql):
Testing:
We have provided you some scripts in testdirectory (under postgresql-8.0.3/). Using these scripts you can check the correctness of your code and play around with different kinds of sampling queries (measure time/io-performance). If you are using instructional machines, use the following commands to setup the pgdata directory for this project (since the databases that we will be creating would be much bigger and will exceed your quota if you use your home directory for pgdata):
If you are using the instructional machines, then use DATADIR as /home/tmp/cs186-??/pgdata (where ??=your class account). Do not use your home directory for pgdata as it will run out of disk space.
We provide you the following scripts:
We encourage you to try more and different kinds of TABLESAMPLE queries than what we have provided.
Measuring IO:
You can find the IO incurred by your query using:
Note, this table keeps track of total IO incurred on the tablename since the database was last started.
Measuring Time:
\timing on psql prompt toggles the timing option.
Project part 2: (30%)
While the TABLESAMPLE feature can be very useful for quick analysis, SQL development, and testing, you should remember that these results reflect sampling of values and not the entire table! A bad choice of these random tuples (or blocks, in the case of SYSTEM sampling) might give us very distorted results. In this part of the project your task is to explore a few scenarios where sampling fails and try to investigate the reasons behind it.
You will be examing 3 scenarios, 2(a), (b) and (c). You will be using a trimmed and slightly modified version of the US government's political party donations database from http://www.fec.gov/finance/disclosure/ftpdet.shtml#2003_2004. Our scripts will set up this database for you. Its schema is described below:
How to run the queries:
In this part of the assignment, you will connect to a postmaster that we have installed on the following SOLARIS x86 instructional machines (replace machine name with one of the following):
Part 2(a) "John Kerry for President Inc " vs "Bush-Cheney '04 Inc." (10%)
These are the two big committees that received a substantial amount of donations from individuals. If you observe the above schema carefully then you will see that individuals donate to committees while committees donate to candidates. To avoid forcing you to look at join queries in this homework, we have already looked up the ids of the above committees for you:
For this subpart your task is to run the following 4 queries and fill in the results table below. For the queries involving sampling, we ask you to run them 10 times with 10 different seeds (1 through 10), and note the result you get each time. The table is provided for your reference and you do not have to turn it in.
| Query | Avg(amount) |
|---|---|
| Q1.no_sample | |
| Q2.no_sample |
Query |
Seed (r) -> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Std Devn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Q1 |
||||||||||||
Q2 |
||||||||||||
For the above table, the last column is the sample standard deviation where mean = 'Qi.no_sample' ? [For details on calculating the sample standard deviation, refer to http://mathworld.wolfram.com/StandardDeviation.html]. PostgreSQL provides the STDDEV aggregate function to compute a standard deviation as well, if you would like to load your results into a database table.
You need to turn in answers to the following questions:
Part 2(b) Ever heard of "The Media Fund Inc" Committee? (10%)
Neither did we! But its committee ID is C30000053.
For this part you will run the following queries and build a
table. Finally you will answer the questions that follow.
| Query | Avg(amount) |
|---|---|
| Q3.no_sample |
Query |
Seed (r) -> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Std Devn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Q3.SYS_SAMPLE |
||||||||||||
Q3.BERN_SAMPLE |
||||||||||||
Again, the last column above stands for sample standard deviation where mean = Q3.no_sample.
If any of the above queries returns a blank, then you can assume it to be a 0. NOTE: This should not affect your answers to the following questions:Part 2(c) Number of candidates from California? (10%)
From the candidates table you can find out that the number of candidates contesting from california were the largest. For this part we want you to run the following queries:
| Query | count(*) |
|---|---|
| Q4.no_sample |
Query |
Percent (p) -> | 1 | 5 | 10 | 20 | 25 | 40 | 50 | 75 |
|---|---|---|---|---|---|---|---|---|---|
Q4.SYS_SAMPLE |
|||||||||
Q4.BERN_SAMPLE |
|||||||||
Note, we are varying the sampling percent in the above query and not the random seed.
Now answer the following questions:
How to submit:
Submitting part 1 Due Oct 11, 2005Create a directory, hw2p1:
Copy the following files to this directory:
Create a directory hw2p2
Create answers.txt and put your responses for part 2(a)[1-3], 2(b)[1-2], 2(c)[1-3] in this file. Limit the total file size to 300 words. We will automatically truncate your reponses after 300 words. To know the number of words in your file run: "wc -w filename" on the command prompt. Be terse and to the point. You need not explain in gory details but highlight the main factors affecting sampling in various scenarios.