Project 3: Logic and Classical Planning
Due: Monday 3/15 at 11:59 pm

Introduction
In this project, you will use/write simple Python functions that generate logical sentences describing Pacman physics, aka pacphysics. Then you will use a SAT solver, pycosat, to solve the logical inference tasks associated with planning (generating action sequences to reach goal locations and eat all the dots), localization (finding oneself in a map, given a local sensor model), mapping (building the map from scratch), and SLAM (simultaneous localization and mapping).
As in previous programming assignments, this assignment includes an autograder for you to grade your answers on your machine. This can be run with the command:
python autograder.py
See the autograder tutorial in Project 0 for more information about using the autograder.
The code for this project consists of several Python files, some of which you will need to read and understand in order to complete the assignment, and some of which you can ignore. You can download all the code and supporting files as a zip archive.
Files you will edit
logicPlan.py |
Where you will put your code for the various logical agents. |
Files you might want to look at
logic.py |
Propsitional logic code originally from https://code.google.com/p/aima-python/ with modifications for our project. There are several useful utility functions for working with logic in here. |
logicAgents.py |
The file that defines in logical planning form the two specific problems that Pacman will encounter in this project. |
pycosat_test.py |
Quick test main function that checks that the pycosat module is installed correctly. |
game.py |
The internal simulator code for the Pacman world. The only thing you might want to look at in here is the Grid class. |
test_cases/ |
Directory containing the test cases for each question |
Files you will not edit
pacman.py |
The main file that runs Pacman games. |
logic_util.py |
Utility functions for logic.py |
util.py |
Utility functions primarily for other projects. |
logic_planTestClasses.py |
Project specific autograding test classes |
graphicsDisplay.py |
Graphics for Pacman |
graphicsUtils.py |
Support for Pacman graphics |
textDisplay.py |
ASCII graphics for Pacman |
ghostAgents.py |
Agents to control ghosts |
keyboardAgents.py |
Keyboard interfaces to control Pacman |
layout.py |
Code for reading layout files and storing their contents |
autograder.py |
Project autograder |
testParser.py |
Parses autograder test and solution files |
testClasses.py |
General autograding test classes |
Files to Edit and Submit: You will fill in portions of logicPlan.py during the assignment. You should submit these files with your code and comments. Please do not change the other files in this distribution or submit any of our original files other than these files.
Evaluation: Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation -- not the autograder's judgements -- will be the final judge of your score. If necessary, we will review and grade assignments individually to ensure that you receive due credit for your work.
Academic Dishonesty: We will be checking your code against other submissions in the class for logical redundancy. If you copy someone else's code and submit it with minor changes, we will know. These cheat detectors are quite hard to fool, so please don't try. We trust you all to submit your own work only; please don't let us down. If you do, we will pursue the strongest consequences available to us.
Getting Help: You are not alone! If you find yourself stuck on something, contact the course staff for help. Office hours, section, and the discussion forum are there for your support; please use them. If you can't make our office hours, let us know and we will schedule more. We want these projects to be rewarding and instructional, not frustrating and demoralizing. But, we don't know when or how to help unless you ask.
Discussion: Please be careful not to post spoilers.
The Expr Class
In the first part of this project, you will be working with the Expr class defined in logic.py to build propositional logic sentences. An Expr object is implemented as a tree with logical operators (∧, ∨, ¬, →, ↔) at each node and with literals (A, B, C) at the leaves. The sentence
(A ∧ B) ↔ (¬ C ∨ D)
would be represented as the tree
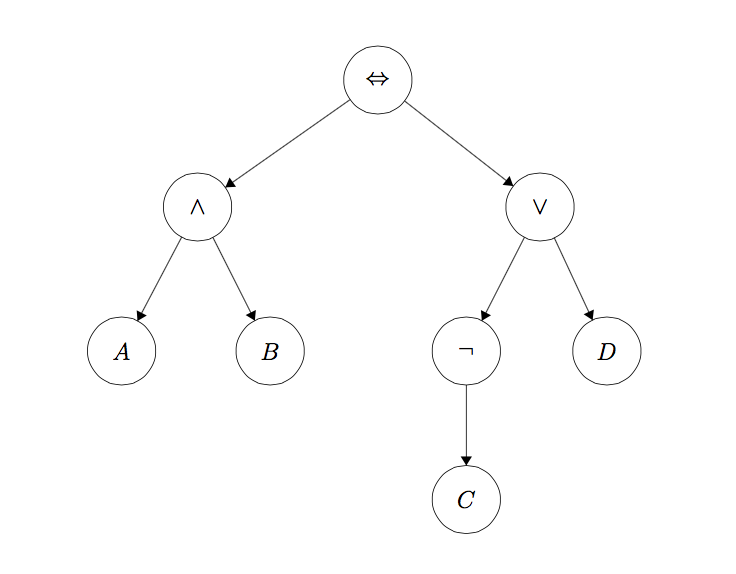
To instantiate a symbol named 'A', call the constructor like this:
A = Expr('A')
The Expr class allows you to use Python
operators to build up these expressions. The following are the available
Python operators and their meanings:
~A: ¬ AA & B: A ∧ BA | B: A ∨ BA >> B: A → BA % B: A ↔ B
So to build the expression A ∧ B, you would type this:
A = Expr('A')
B = Expr('B')
a_and_b = A & B
(Note that A to the left of the assignment operator in that example is just a Python variable name, i.e. symbol1 = Expr('A') would have worked just as well.)
One last important thing to note is that typing in A & B & C will give the expression ((A & B) & C). If instead you want (A & B & C), as you will for these problems, use conjoin, which takes a list of expressions as input and returns one expression that is the conjunction of all the inputs. Even though both expressions are logically equivalent, it is generally neater to use conjoin everywhere you can, because it is easier to read your knowledge base for debugging when your expression tree is more flat and does not have many layers of nested parentheses. The & operator in Python is a binary operator and builds an unbalanced binary tree if you chain it several times, whereas conjoin builds a tree that is one level deep with all the inputs extending directly from the & operator at the root. disjoin is similarly defined for |. The autograder for Question 1 will require that you use conjoin and disjoin wherever possible, instead of chaining several & operators or several |
operators. If you keep with this convention for later problems, it will
help with debugging because you will get more readable expressions.
There is additional, more detailed documentation for the Expr class in logic.py.
Tips
- When creating a symbol with
Expr, it must start with an upper case character. You will get non-obvious errors later if you don't follow this convention. - Be careful creating and combining
Exprinstances. For example, if you intend to create the expressionx = Expr('A') & Expr('B'), you don't want to accidentally typex = Expr('A & B'). The former will be a logical expression of the symbol 'A' and the symbol 'B', while the latter will be a single symbol (Expr) named 'A & B'.
SAT Solver Setup
A SAT (satisfiability) solver takes a logic expression which encodes the rules of the world and returns a model (true and false assignments to logic symbols) that satisfies that expression if such a model exists. To efficiently find a possible model from an expression, we take advantage of the pycosat module, which is a Python wrapper around the picoSAT library.
Unfortunately, this requires installing this module/library on each machine.
To install this software on your conda env, please follow these steps:
- Activate your conda env:
conda activate cs188(if your env is calledcs188) - Install pycosat: On command line run:
pip install pycosat. (Note: you may need to run:sudo pip3 install pycosat.) If you get errors, try insteadconda install -c anaconda pycosat.
Testing pycosat installation:
After unzipping the project code and changing to the project code directory, run:
python pycosat_test.py
This should output:
[1, -2, -3, -4, 5].
Please let us know if you have issues with this setup. This is critical to completing the project, and we don't want you to spend your time fighting with this installation process.
Question 1 (2 points): Logic Warm-up
This question will give you practice working with the Expr data type used in the project to represent propositional logic sentences. You will implement the following functions in logicPlan.py:
sentence1(): Create oneExprinstance that represents that the following three sentences are true. Do not do any logical simplification, just put them in a list in this order, and return the list conjoined. Each element of your list should correspond to each of the three sentences.sentence2(): Create oneExprinstance that represents that the following four sentences are true. Again, do not do any logical simplification, just put them in a list in this order, and return the list conjoined.sentence3(): Using thePropSymbolExprconstructor, create symbolsPacmanAlive[0],PacmanAlive[1],PacmanBorn[0], andPacmanKilled[0](see below for an examplePropSymbolExprinstantiation), and create oneExprinstance which encodes the following three English sentences as propositional logic in this order without any simplification:- Pacman is alive at time 1 if and only if he was alive at time 0 and he was not killed at time 0 or he was not alive at time 0 and he was born at time 0.
- At time 0, Pacman cannot both be alive and be born.
- Pacman is born at time 0.
findModel(sentence): Useto_cnfto convert the input sentence into Conjunctive Normal Form (the form required by the SAT solver). Then pass it to the SAT solver usingpycoSATto find a satisfying assignment to the symbols insentence, i.e., a model. A model is a dictionary of the symbols in your expression and a corresponding assignment of True or False. You can test your code onsentence1(),sentence2(), andsentence3()by opening an interactive session in Python and runningfindModel(sentence1())and similar queries for the other two. Do they match what you thought?
A ∨ B
¬ A ↔ (¬ B ∨ C)
¬ A ∨ ¬ B ∨ C
C ↔ (B ∨ D)
A → (¬ B ∧ ¬ D)
¬ (B ∧ ¬ C) → A
¬ D → C
For the later problems in the project, we will have symbols with names like P[3, 4, 2], which represents Pacman being at position (3, 4) at time 2, and we will use them in logic expressions like the above in place of A, B, C, D. The PropSymbolExpr constructor is a useful tool for creating symbols like P[3, 4, 2] that have numerical information encoded in their name. For example, to obtain the symbol P[3,4,2], you would type PropSymbolExpr('P', 3, 4, 2).
Are sentence1(), sentence2(), and sentence3() satisfiable? If so, try to find a satisfying assignment. (This is not graded, but is a good self-check to make sure you understand what's happening here.)
Before you continue, try instantiating a small sentence, e.g. A ∧ B → C, and call to_cnf on it. Inspect the output and make sure you understand it (refer to AIMA section 7.5.2 for details on the algorithm to_cnf implements).
To test and debug your code run:
python autograder.py -q q1Question 2 (2 points): Logic Workout
Implement the following three logic expressions in logicPlan.py:
atLeastOne(literals): Return a single expression (Expr) in CNF that is true only if at least one expression in the input list is true. Each input expression will be a literal.atMostOne(literals): Return a single expression (Expr) in CNF that is true only if at most one expression in the input list is true. Each input expression will be a literal. HINT: Useitertools.combinations. If you have `n` literals, and at most one is true, your resulting CNF expression should be a conjunction of $n \choose 2$ clauses.exactlyOne(literals): Return a single expression (Expr) in CNF that is true only if exactly one expression in the input list is true. Each input expression will be a literal. If you decide to call your previously implementedatLeastOneandatMostOne, callatLeastOnefirst to pass our autograder for q3.
Each of these methods takes a list of Expr literals and returns a single Expr
expression that represents the appropriate logical relationship between
the expressions in the input list. An additional requirement is that
the returned Expr must be in CNF (conjunctive normal form). You may NOT use the to_cnf function in your method implementations (or any of the helper functions logic.eliminate_implications, logic.move_not_inwards, and logic.distribute_and_over_or).
When implementing your planning agents in the later
questions, you will not have to worry about CNF until right before
sending your expression to the SAT solver (at which point you can use findModelfrom question 1). to_cnf
implements the algorithm from section 7.5 in AIMA. However, on certain
worst-case inputs, the direct implementation of this algorithm can
result in an exponentially sized sentences. In fact, a certain non-CNF
implementation of atMostOne is one such worst case.
So if you find yourself needing the functionality of atLeastOne, atMostOne, or exactlyOne
for a later question, make sure to use the functions you've already
implemented here to avoid accidentally coming up with that non-CNF
alternative and passing it to to_cnf. If you do this, your code will be so slow that you can't even solve a 3x3 maze with no walls.
You may utilize the logic.pl_true function to test the output of your expressions. pl_true takes an expression and a model and returns True if and only if the expression is true given the model.
To test and debug your code run:
python autograder.py -q q2
Question 3 (3 points): Pacphysics and Satisfiability
In this question, you will implement the basic pacphysics logical expressions, as well as learn how to prove where pacman is and isn’t by building an appropriate knowledge base (KB) of logical expressions.
Implement the following functions in logicPlan.py:
pacphysics_axioms: Here, you will add the following axioms topacphysics_sentences. For a given timestep t:- For all (x, y) in
all_coords, add the following implication (if-then form): if a wall is at (x, y), then Pacman is not at (x, y, t) - Pacman is at exactly one of the
non_outer_wall_coordsat timestep t. - Pacman takes exactly one of the four actions in
DIRECTIONSat timestep t. - Add each of the sentences above to
pacphysics_sentences. check_location_satisfiability: Given a transition (x0_y0, action0, x1_y1, action1) and aproblem, you will write a function that will return a tuple of two models(model1, model2).model1will attempt to prove that givenx0_y0, action0, action1, Pacman is at (x1, y1) at time t = 1.model2will attempt to prove that givenx0_y0, action0, action1, Pacman is NOT at (x1, y1) at time t = 1.- To implement this problem, you will need to add the following expressions to your KB in order:
- At t = 0:
- Add to KB: Pacman’s current location (x0, y0)
- Add to KB:
pacphysics_axioms(...) - Add to KB: Pacman takes
action0 - Add to KB:
allLegalSuccessorAxioms(t+1, ...) - At t = 1:
- Add to KB:
pacphysics_axioms(...) - Add to KB: Pacman takes
action1
If you are stuck on check_location_satisfiability, think back to WHW2 about how to prove a knowledge base entails some query q: we prove that KB ∧ ¬ q is unsatisfiable. Likewise, to prove some query q is false given a knowledge base, we prove KB ∧ q is unsatisfiable. Thus, your two models should both call findModel, but one on KB ∧ (Pacman at (x1, y1)), and the other on KB ∧ ¬ (Pacman at (x1, y1)).
Prop Symbol Names (Important!): For the rest of the project, please use the following variable naming conventions:
PropSymbolExpr(pacman_str, x, y, t): whether or not Pacman is at (x, y) at time tPropSymbolExpr(wall_str, x, y): whether or not a wall is at (x, y)PropSymbolExpr(action, t): whether or not pacman takes actionactionat time t, whereactionis an element ofDIRECTIONS
PropSymbolExpr(pacman_str, x, y, t). For the variable that encodes whether or not a wall is at (x, y), write the code PropSymbolExpr(wall_str, x, y).
Transition Models: In this project, we will use two different transition models:
allLegalSuccessorAxioms: This transition model assumes that all actions taken are valid (no action brings pacman onto a square with walls). We will use this function to generate our successor axioms for most of the project, because it is lightweight and improves runtime.SLAMSuccessorAxioms: This transition model does not assume all actions taken are valid, which adds a lot of computational overhead. We will use this function to generate successor axioms only for the SLAM problem.
Something to keep in mind for the rest of the project: in the localization and mapping problems later in the project, we will use a 4-bit sensor (which indicates whether there is or isn’t a wall in the NSEW directions of Pacman) with allLegalSuccessorAxioms. However for SLAM, we will use a weaker sensor (that only tells us the number of walls adjacent to Pacman) with SLAMSuccessorAxioms.
To test and debug your code run:
python autograder.py -q q3
Question 4 (4 points): Path Planning with Logic
Pacman is trying to find the end of the maze (the goal position). Implement the following method using propositional logic to plan Pacman's sequence of actions leading him to the goal:
positionLogicPlan(problem): Given an instance oflogicPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.
You will not be implementing a search algorithm, but creating expressions that represent pacphysics for all possible positions at each time step. This means that at each time step, you should be adding general rules for all possible locations on the grid, where the rules do not assume anything about Pacman's current position.
You will need to code up the following sentences for your knowledge base, in the following pseudocode form:
- Add to KB: Initial knowledge: Pacman's initial location at timestep 0
- for t in range(50) [Autograder will not test on layouts requiring `ge` 50 timesteps]
- Add to KB: Initial knowledge: Pacman can only be at
exactlyOneof the locations innon_wall_coordsat timestep t. - Is there a satisfying assignment for the variables given the knowledge base so far? Use
findModeland pass in the Goal Assertion andKB. - If there is, return a sequence of actions from start to goal using
extractActionSequence. - Here, Goal Assertion is the expression asserting that Pacman is at the goal at timestep t.
- Add to KB: Pacman takes exactly one action per timestep.
- Add to KB: Transition Model sentences: call
pacmanSuccessorStateAxioms(...)for all possible pacman positions innon_wall_coords.
Test your code on smaller mazes using:
python pacman.py -l maze2x2 -p LogicAgent -a fn=plp
python pacman.py -l tinyMaze -p LogicAgent -a fn=plp
To test and debug your code run:
python autograder.py -q q4
Note that with the way we have Pacman's grid laid out, the leftmost, bottommost space occupiable by Pacman (assuming there isn't a wall there) is (1, 1), as shown below (not (0, 0)).
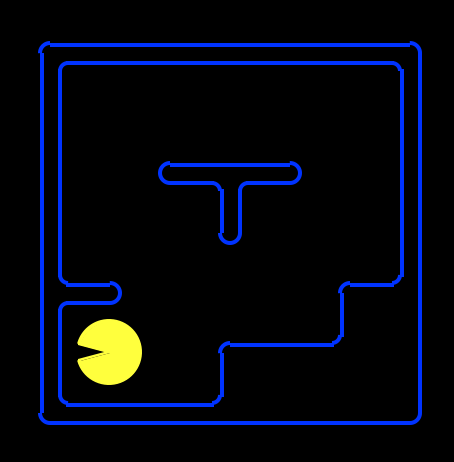
Hint: If you are stuck, try re-reading AIMA chapter 7.7, "Agents Based on Propositional Logic." The pacphysics are also laid out in Lecture 11.
Debugging hints:
- If you're finding a length-0 or a length-1 solution: is it enough to simply have axioms for where Pacman is at a given time? What's to prevent him from also being in other places?
- Coming up with some of these plans can take a long time. It's useful to have a print statement in your main loop so you can monitor your progress while it's computing.
- If your solution is taking more than a couple minutes to finish running, you may want to revisit implementation of
exactlyOneandatMostOne(if you rely on those), and ensure that you're using as few clauses as possible.
Question 5 (3 points): Eating All the Food
Pacman is trying to eat all of the food on the board. Implement the following method using propositional logic to plan Pacman's sequence of actions leading him to the goal.
foodLogicPlan(problem): Given an instance oflogicPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.
This question has the same general format as question 4. The notes and hints from question 4 apply to this question as well. You are responsible for implementing whichever successor state axioms are necessary that were not implemented in previous questions.
What you will change from the previous question:
- Initialize Food[x,y,t] variables with the code
PropSymbolExpr(food_str, x, y, t), where each variable is true iff there is a food at (x, y) at time t. - Change the goal assertion: Your goal assertion sentence must be true iff all of the food have been eaten. This happens when all Food[x,y,t] are false at time t.
- Add a food successor axiom: What is the relation between Food[x,y,t+1] and Food[x,y,t] and Pacman[x,y,t]? The food successor axiom should only involve these three variables, for any given (x, y, t). Think about what the transition model for the food variables looks like, and add these sentences to your knowledge base at each timestep.
Test your code using:
python pacman.py -l testSearch -p LogicAgent -a fn=flp,prob=FoodPlanningProblem
We will not test your code on any layouts that require more than 50 time steps.
To test and debug your code run:
python autograder.py -q q5
Helper Functions for the rest of the Project
For the remaining questions, we will rely on the following helper functions, which will be referenced by the pseudocode for localization, mapping, and SLAM.
Add pacphysics, action, sensor, and percept information to KB
- Add to KB:
pacphysics_axioms(...), which you wrote in q3. - Add to KB: Pacman takes action prescribed by
agent.actions[t] - Add to KB: either
sensorAxioms(...)for localization and mapping, orSLAMSensorAxioms(...)for SLAM. - Get the percepts by calling
agent.getPercepts()and pass the percepts tofour_bit_percept_rules(...)for localization and mapping, ornum_adj_walls_percept_rules(...)for SLAM. Add the resulting percept_rules toKB.
Find possible pacman locations with updated KB
possible_locations_t = []- Iterate over
non_outer_wall_coords. - Can we prove whether Pacman is at (x, y)? Can we prove whether Pacman is not at (x, y)? Use
findModeland theKB. Think about how you did this in question 3. - If there exists a satisfying assignment where Pacman is at (x, y) at time t, add (x, y) to
possible_locations_t. - Add to KB: (x, y) locations where Pacman is provably at, at time t.
- Add to KB: (x, y) locations where Pacman is provably not at, at time t.
- Append
possible_locations_ttopossible_locs_by_timestep.
Find provable wall locations with updated KB
- Iterate over
non_outer_wall_coords. - Can we prove whether a wall is at (x, y)? Can we prove whether a wall is not at (x, y)? Use
findModeland theKB. Think about how you did this in question 3. - Add to KB and update
known_map: (x, y) locations where there is provably a wall. - Add to KB and update
known_map: (x, y) locations where there is provably not a wall. - Append
copy.deepcopy(known_map)toknown_map_by_timestep.
Question 6 (4 points): Localization
Pacman starts with a known map, but unknown starting location. It has a 4-bit sensor that returns whether there is a wall in its NSEW directions. (For example, 1001 means there is a wall to pacman's North and West directions, and these 4-bits are represented using a list with 4 booleans.) By keeping track of these sensor readings and the action it took at each timestep, Pacman is able to pinpoint its location. You will code up the sentences that help Pacman determine the possible locations it can be at each timestep by implementing:
localization(problem, agent): Given an instance oflogicPlan.LocalizationProblemand an instance oflogicAgents.LocalizationLogicAgent, returns a list of lists: [[(x_0_0, y_0_0), (x_1_0, y_1_0), ...], [...], ...], where [(x_i_t, y_i_t), ...] is a list of possible pacman locations (x_i, y_i) at time t.
For Pacman to make use of sensor information during localization, you will use two methods already implemented for you: sensorAxioms, which are the axioms listed won slide 4 of lecture 10, and four_bit_percept_rules, which translate the percepts at time t into logic sentences.
To pass the autograder, please implement the function according to our pseudocode:
- Add to
KB: where the walls are (walls_list) and aren't (not inwalls_list). - for t in
range(agent.num_timesteps): - Add pacphysics, action, sensor, and percept information to KB.
- Find possible pacman locations with updated KB.
- Call
agent.moveToNextState(...)on the current agent action at timestep t. - Add to
KB:allLegalSuccessorAxioms(...). - return
possible_locs_by_timestep
Note (i): We take this step because adding unit literals to the KB help speed up future inferences.
If you are stuck on the "Find possible pacman locations with updated KB" step, think about what you did in the satisfiability function in question 3.
To test and debug your code run:
python autograder.py -q q6
Question 7 (3 points): Mapping
Pacman now knows his starting location, but does not know where the walls are (other than the fact that the border of outer coordinates are walls). Similar to localization, it has a 4-bit sensor that returns whether there is a wall in its NSEW directions. You will code up the sentences that help Pacman determine the location of the walls by implementing:
mapping(problem, agent): Given an instance oflogicPlan.MappingProblemand an instance oflogicAgents.MappingLogicAgent, returnsknown_maps_by_timestep, a list ofknown_maps of format [known_map_0, known_map_1, ...], where:- known_map_t is a 2D-array (list of lists) of size (problem.getWidth()+2, problem.getHeight()+2)
- Each entry of known_map_t is 1 if (x, y) is guaranteed to be a wall at timestep t, 0 if (x, y) is guaranteed to not be a wall, and -1 if (x, y) is still ambiguous at timestep t
- Ambiguity results when one cannot prove that (x, y) is a wall and one cannot prove that (x, y) is not a wall.
To pass the autograder, please implement the function according to our pseudocode:
- Get initial location
(pac_x_0, pac_y_0)of Pacman, and add this toKB. - for t in
range(agent.num_timesteps): - Add pacphysics, action, sensor, and percept information to KB.
- Find provable wall locations with updated KB
- Call
agent.moveToNextState(...)on the current agent action at timestep t. - Add to
KB:allLegalSuccessorAxioms(...). - return
known_map_by_timestep
To test and debug your code run:
python autograder.py -q q7
Question 8 (4 points): SLAM
Sometimes Pacman is just really lost and in the dark at the same time. In SLAM (Simultaneous Localization and Mapping), Pacman knows his initial coordinates, but does not know where the walls are. In SLAM, Pacman may inadvertently take illegal actions (for example, going North when there is a wall blocking that action), which will add to the uncertainty of Pacman's location over time. Additionally, in our setup of SLAM, Pacman no longer has a 4 bit sensor that tells us whether there is a wall in the four directions, but only has a 3-bit sensor that reveals the number of walls he is adjacent to. (This is sort of like wifi signal-strength bars; 000 = not adjacent to any wall; 100 = adjacent to exactly 1 wall; 110 = adjacent to exactly 2 walls; 111 = adjacent to exactly 3 walls. These 3 bits are represented by a list of 3 booleans.) Thus, instead of using sensorAxioms and four_bit_percept_rules, you will use SLAMSensorAxioms and num_adj_walls_percept_rules. You will code up the sentences that help Pacman determine (1) his possible locations at each timestep, and (2) the location of the walls, by implementing:
slam(problem, agent): Given an instance oflogicPlan.SLAMProblemandlogicAgents.SLAMLogicAgent, returns a tuple of two items:- list of known_maps per timestep (of the same format as in question 6 (mapping))
- list of possible pacman locations per timestep (of the same format as in question 5 (localization))
To pass the autograder, please implement the function according to our pseudocode:
- Get initial location
(pac_x_0, pac_y_0)of Pacman, and add this toKB. - for t in
range(agent.num_timesteps): - Add pacphysics, action, sensor, and percept information to KB.
- Find provable wall locations with updated KB
- Find possible pacman locations with updated KB.
- Call
agent.moveToNextState(...)on the current agent action at timestep t. - Add to
KB:SLAMSuccessorAxioms(...). - return
known_map_by_timestep, possible_locs_by_timestep
To test and debug your code run:
python autograder.py -q q8
Submission
In order to submit your project, run python submission_autograder.py and submit the generated token file logic.token to the Project 3 assignment on Gradescope.