Proj 4: Facial Morphing

Technical Implementation

For this project, we consider faces as a linear subspace. This means that we can interpolate and extrapolate between faces when they are given as image matrices. To do so, we first define keypoints on each face. These keypoints are averaged to create midway keypoints, which are tesselated into a Delaunay triangulation. We choose a Delaunay triangulation, because it minimizes the maximum angle in each triangle.


From the midway Delaunay triangulation, we have a base set of triangles that we want both faces to morph to. Morphing from a source face to the average face is as simple as multiplying the source face on the left by a transformation matrix. Because we are working with triangles, which means three points to transform, our transformation is an affine one.

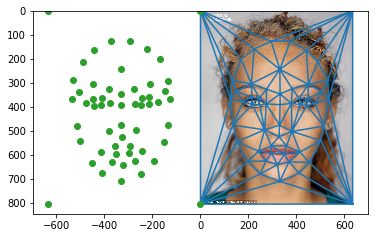This the average triangulation juxtaposed/overlaid with one source image.

However, because we are dealing with images, we only have (x,y) coordinates initially. With only two points, we are not able to capture a degree of freedom that represents translation. Therefore, we loft these (x,y) coordinates into 3D, so that each (x,y) becomes (x,y,1). Now, we can solve any transform + translation of triangle A to triangle B.

Intuitively, we would want to calculate the transformation T that goes from source A to average B (T(A) = B), and apply T to every pixel bounded by the triangle in A. This would give us a (x',y') coordinate in B that would take on (x,y)'s value. However, because T is solved for and can contain floats, T(A) is a matrix of floats as well--which means that these new (x',y') coordinates could land in between pixels. This is a problem known as splatting.

To resolve this, we use an inverse warp, which solves for the inverse of T. By solving for the inverse of T and applying this inverse affine transform to every coordinate in B (the destination image/average face), our resulting image can avoid splatting. Even when the pixel lands in between some coordinate in the source face, we simply interpolate within that source neighborhood.

By iterating through every pair of triangles, and calculating for each pixel in the destination/average image, we are able to produce a midway face--the third image in the image row above.

Creating the morph sequence thereafter is simple. We just linearly interpolate between two factors--the warp fraction and the dissolve fraction. The steps prior, which revolved around the midway face, used a Delaunay triangulation that relied on the average of the two source faces. The warp fraction changes the average to a weighted average. The dissolve fraction changes the averaging of the colors into a weighted average as well.

Thus by concatenating the linearly interpolated frames, we are able to create facial morphing. All these steps above summarize the two steps of creating an average object: warp images to an average shape and then cross dissolve the colors.
So here is the final result again.

Average of a subpopulation

The population and dataset that I chose to use was the males from the Danes facial database. From the 33 images, I was able to create this average Danish male computer scientist.
To do so, I warped each Danish male to average shape calculated from the average of all their facial keypoints. Here are a few examples of how some of the males looked post-warping.

Caricature

We are not limited to interpolating between two faces. We can treat faces as vectors add and subtract to them as we like since we are in a subspace. If we treat the difference between a face and the average as a vector subtraction (Face X - subpopulation average), we have a quantitative correlate for the uniqueness of the face. If we add this difference back into the averaged keypoints at different weights, we can create various levels of caricaturization.


(I've seen so many warped faces now that I feel like even normal faces are warped.)

Bells and Whistles

I decided to morph on two themes: 1) movie posters 2) art.

Silence of the Lambs

Titanic

I found an old picture of my aunt, who used to be a model. She was modeling hats in this old photograph, and I thought the angle quite like Kate Winslet's here, so I morphed them together.

Moroccan Art

I also thought it would be interesting to explore other subspaces, such as Islamic geometric art. These are some Moroccan tile patterns, morphed to their neighbors in a kaleidoscope fashion.

Animating Keyframes

I wondered what it would be like to try animating keyframes--to see how far I could push the correspondences. Unfortunately, as you can see from this failure case below...you can't really work with images that aren't contained in a subspace.

Art Nouveau

And lastly, because I was recently introduced to Alphonse Mucha's stylized art Nouveau / art deco work, I wanted to morph some of his work. But it was only mildly successful.