Project 4: Face Morphing

In this project, I experiment with some more facial manipulations!

To start off... EVERYONE thinks I look like Mark Zuckerberg. I'm going to prove them wrong with triangles.

Part 0: Correspondences

Since I will eventually be focusing on calculating a "mean face" from the population, I figured why not go ahead and download some data for that. The key here is to use "points of correspondence". That is, one facial image will have a set of human-picked points of importance A, and another facial image will have a set B whose points correspond to those in A. For example, the first four points in A might correspond to the lips. B's first four points must also then correspond to the lips.

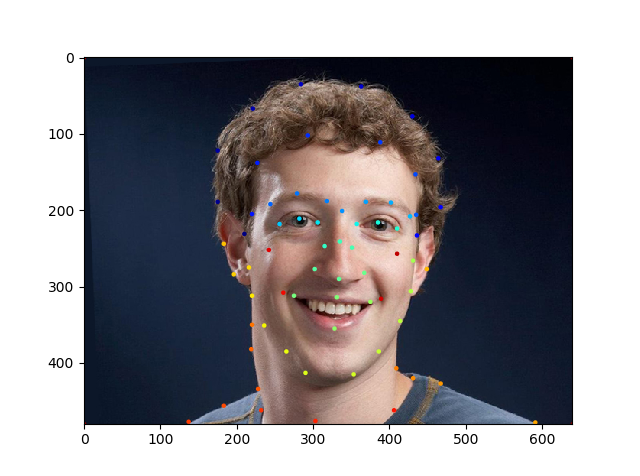
I chose to use data from a professor at DTU (The Technical University of Denmark) that has some pre-defined points of correspondence, as well as a special file that defines these points called ASF files. My main goal was to make a parser for these files and then test the points. Here is the result on the first image in the dataset...

REF: M. B. Stegmann, B. K. Ersbøll, and R. Larsen. FAME – a flexible appearance modelling environment. IEEE Trans. on Medical Imaging, 22(10):1319–1331, 2003

Note that I colored these points in a rainbow to indicate their position in their correspondence set. That is, blue == early and red == late.

Now with an ASF parser, I defined some custom points on my face and on Mark Zuckerberg's face. These points are saved and will be quite important later.

Now, I take the midpoints of all the points of correspondence between Gibbes and Zuck and construct a Delaunay triangulation over them. Currently, I am using the scipy.spatial.Delaunay to construct the triangles from this set of points. The gist of these triangles is that they are the most "regular" -- skinny triangles will result in weird transformations.

Part 1: Computing the "Mid-Way Face"

Using the simplices (vertices of the triangle defined by indices of points) defined by the Delaunay points, I'm going to try to warp the triangles from my face towards Zuckerberg's face. This is my approach to implementation:

1. Iterate through the triangles. Note that each triangle in Gibbes has a corresponding triangle in Zuckerberg.
2. Compute the affine transform from the triangle in the Gibbes image to the triangle in the Zuckerberg image.
3. For each point in the target image, use the affine transformation to find the corresponding point in the source image. (This takes care of triangles having different sizes.)

The result of applying these transformations to the mid-way point is shown below on each of the images.

The result of taking the average of the previous two images is a true treat to the eye.

Part 2: The Morph Sequence

I don't really have much to say about this part except that I wrote an outer "encapsulator" function for drawing frames that interpolates between 0 to 1, drawing intermediate triangles that get used in my previous warp function. Really, not much different here from computing the midway face.

The final result is even more a treat to the eye. That graceful emotional transform, too...

Actually, this seems to have only reinforced the belief that I look like him...

Part 3: The "Mean Face" of the Danes

Using 38 faces from the Danes population, I managed to create an "average" face. This average was computed by...

1. Averaging all points into an average set of points by summing and dividing by 38, then triangulating over the average.
2. Warping each image towards the average, then accumulating it into an image by a factor of 1/38.

The result...

Note that this particular data set leans towards masculine faces, so the result will inevitably be more masculine.

Using this average face and its set of average points, we can now mess around with individual facial data. The results seen below are taken from the Danish set, and they might seem a bit extreme, as each point set was warped 100% towards the other point set.

Using the computed average face from the Danish set worked interestingly on non-Danish participants (me and my friend, Mumu):

Part 4: Caricature

Not much more to say here, except that if you use warp the faces in the "backwards" direction (i.e. instead of warping towards the average, warp away from the average), you get some interesting results. Here is the effect on me and Mumu, using the same data from the previous part. Most of the background is removed because I didn't want to include points on the edge due to the possibility that the triangles go out of the image.

Very flattering. Mumu even drew her own version of the picture outputted by the caricature algorithm:

Part 5: Bells and Whistles

Really just a spot where I'm going to mess around with the triangulation algorithm described above.

Anime Morph

As an experiment, I tried mixing a real face with an anime face. The result is actually quite interesting, as the mid-way face almost appears cel shaded -- that is, the type of shading in animation and video games where edge boundaries have thick lines.

Mass Morphing

Additionally, a team of 24 students got together to make a long morph transition across our faces. The result: