
The goals of this project are to produce a "morph" animation of mt own face into someone else's face, compute the mean of a population of faces and extrapolate from a population mean to create a caricature of myself. A morph consists of a simultaneous warp of shape and a cross-dissolve of image color. A cross-dissolve is simply a weighted average of pixel intensities. However, a warp of shape is more involved; we must correspondences between images.
A correspondence is a pair of corresponding points in two images. These points points provide a way to represent the shape of an image. For the morph, the goal is to gradually change from the shape of our source image to the shape of our target image. A global warp is not sufficient for this purpose. Instead, we can compute a Delauny triangulation using the correspondences, and apply local warps to pixels depending on a triangulation. Below is an example triangulation using the shape of my own face:

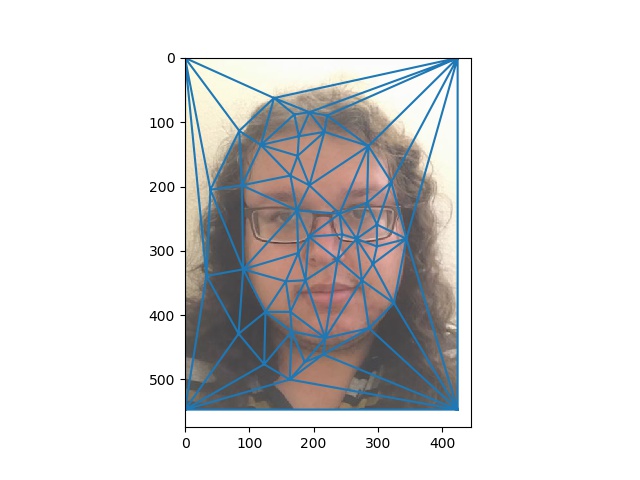
For any sort of face morphing, it makes more sense to compute a triangulation on an intermidate shape rather than one of the original images.
Before computing a completely fluid warp from my face to another, it is simply to consider the Mid-Face. To do this, I implement an inverse warping algorithm. This works by:



To create a morph sequence, I just run the same inverse warping algorithm that produced the mean face, but taking care to adjust the warping fraction t and the crossdissolve fraction tf to vary (45 values evenly space from [0, 1]). I then took each of the resulting 45 frames and made a gif with them. Below are the results:



Creating the mean face of a population is similiar to the previous two parts. It only required keeping track of more images and more affine transformations. For this part, I took the average of all the points in the Danes image database as the average shape, and the average pixel intensites for my crossdissolve. Below is my calculated mean face:

I also decided to warp the 1st and the 20th image in the database back into the population mean face:




And finally, I project my own face onto the average geometery of the mean Danes face and show the resulting midface, effectively changing my ethnicity:


Using the mean face computing from the previous part, I can also create caricatures by extrapolating using values for the warp fraction out of the range(0, 1). Below are the results of my algorithm:






The results do not look as good as I had hoped. As I extrapolate further from initial bounds of the morph, certain things such as a lighting, the angle of my eyes, as well as the roundess of my face become more apparaent, as these are features that were present in the Danes Database. Perhaps if I had choosen a different picture or a more similiar population, things might have been better. However, I am still satisfied with the results.
In part 3, I previously performed an inverse warp and cross-dissolve to the Danes Image DataBase (both males and females), which effectively changed my ethnicity:

However, I did not look at the results of apply an inverse warp and cross-dissolve individually. Below I display the only results from the inverse warp, which gives me the average shape, and the cross-dissolve, which gives me the average apperance:


Funnily enough, the cross-dissolve ended up looking better than the combination of the inverse warp and cross dissolve (despite not being the average object). This really just goes to show the allignment of the images really does effect results.