Part 1: Introduction

The goal of this project was to perform transformations between faces, using morphing as well as using population means. Each method requires defining correspondences manually on an input face, and using affine transformations to transform one shape derived from the corresponding points to another shape. The resulting image would then take weighed averages between the pixels in the original image and pixels in a reference image.

Part 2: Defining Correspondences

Correspondences were defined manually by picking points on two images such that they corresponded to equivalent features. Input images, and the points defined are as shown

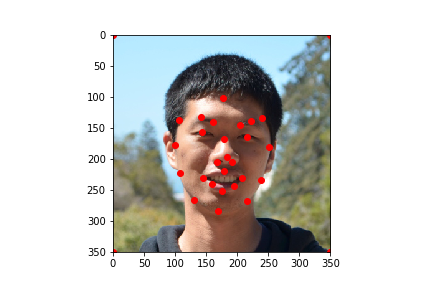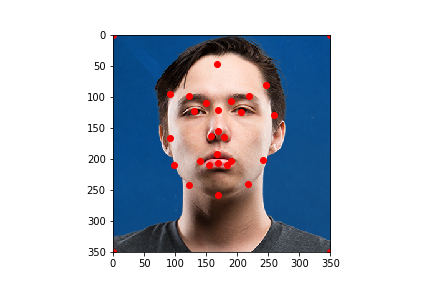Computing the midway face

From the 2 correspoding points, a "midway" shape was defined by simply averaging the 2 corresponding points from the same locations. A delaunay triangulation was defined on the midway shape, and both faces were morphed into that shape. Finally, the pixel values from the 2 morphed images were averaged to compute the midway face.

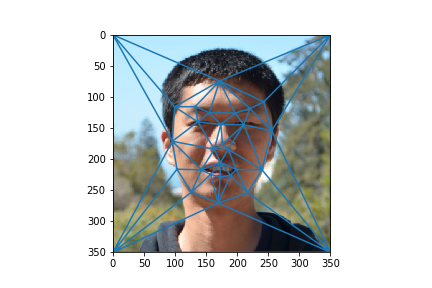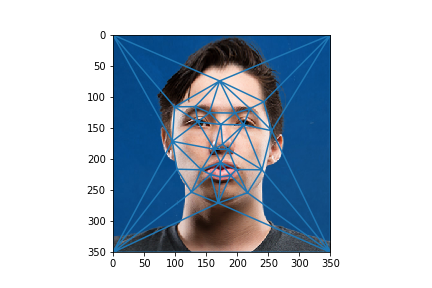Part 3: Morph Sequence

The morph sequence was generated in a similar manner to the midway face. For each frame 0-45, a warp and dissolve fraction was defined to be proportional to the frame number. For this case, the two are equivalent. Then, instead of taking an equal ratio of both images for both the shape and the pixel values, a weighed average of the shape and pixels were taken corresponding to the warp and dissolve fractions respectively. When each frame is put together, we get a nice morph sequence

The "Mean Face" of a population

To generate the "mean face" of a population, we first received a collection of face images, each annotated with corresponding points. Source: M. B. Stegmann, B. K. Ersbøll, and R. Larsen. FAME – a flexible appearance modelling environment. IEEE Trans. on Medical Imaging, 22(10):1319–1331, 2003

An average face of the subpopulation consisting of faces with neutral expressions was computed by first averaging the shapes of each face, and morphing each face into that shape. Then, each morphed face is average together.

In addition to computing the average face, I decided to annotate my own face corresponding to the face dataset, and morphed my face to the average face, and the average face to my face. The results don't look as good because of manual error in my own annotations.

Caricatures: Extrapolating from the mean

A caricature of my face was generated by extrapolating my face's shape from the population mean. My face was then morphed into the extrapolated shape. The results look wacky due to the difficulty in accurately annotating the points. However, we can see a couple of caricatured elements, including larger lips, larger teeth, and larger nose

Bells and Whistles, Unsmiling a face

To unsmile myself, I took subpopulation means of smiling people and not smiling people, and added the difference between unsmiling and smiling people to my face in different ways. I first added just the difference in shape, then the difference in pixel colors, then added both the difference in shape and color.