Ajay Ramesh, October 18, 2018
Face Morphing
Overview
In this project we learned how to warp one face to another. Instead of merely cross fading, this method actually changes the facial structure.
We used Delaunay triangulation, estimation of affine transforms, and 2D interpolation to achieve the effects presented.
Defining Correspondences
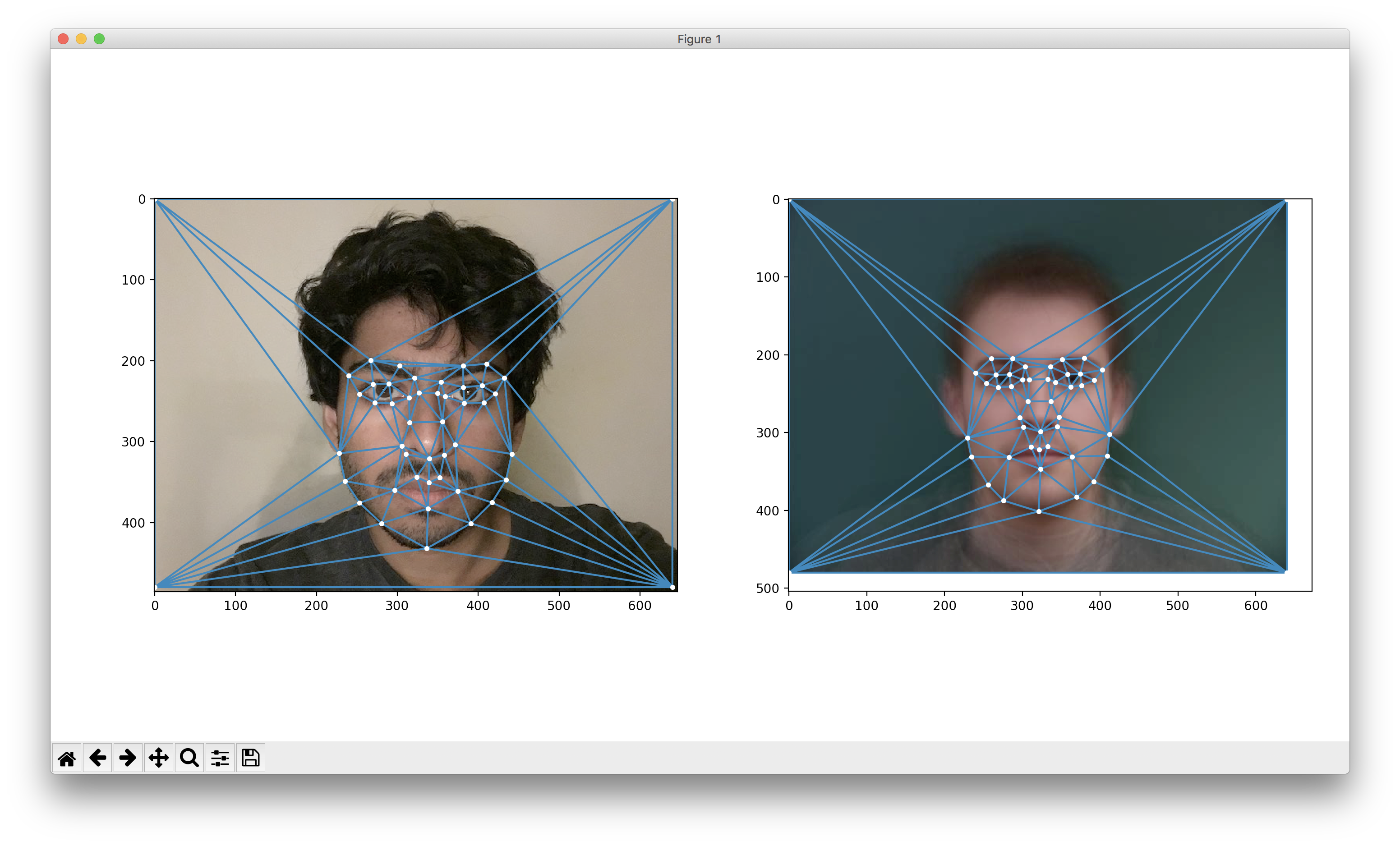
We require corresponding features on the face we are warping from, and the face we are warping to. These correspondences are
used to compute Delaunay triangulations of the faces. These triangulations are used to compute affine transforms of pixels from one
face to another. For the images I labeled myself, I used cpselect in MATLAB.

Computing the Midway Face
In order to compute the midway face, we find the "average face" by finding the average x positions and average y positions of the corresponding
features on each of the source images. Then, we warp both images to the same average face, and finally average the color intensities.
Source A
 Source B
Source B
 Midway Face
Midway Face

Morph Sequence
We used face data from MIT CSAIL to generate these morphs. The morphs are generated by varying
the weight of each of the source image feature locations, as well as the color intensities. This can be expressed as (1-t)A + tB where t is the
parameter we are varying and A and B can either be matrices of feature points, or images themselves.
This particular data set only labels the face, and omits hair and other background objects. To observe the morph, focus on facial features like the mouth, eyes, and eyebrows.
Mean Face of a Population
We used the Danes data set to estimate the mean face of all forward facing males
in the data set. Computing the mean facial structure of the population reduces to averaging all the x and y coordinates of of every face in the population
we are measuring. To produce the image, we warp the image of each person in the data set, to the average face, and simply average the pixel intensities.
Faces warped to mean face



Mean of 37 Faces

Ajay warped to Mean Face

Mean warped to Ajay

Caricatures
In order to create a caricature, we can extrapolate from the mean by weighting one of the facial structures with a weight greater than 1, and weighting the
other facial structure with a weight less than 0. This is equivalent to finding the difference vector between two vectors, and adding a positive weight of the
difference vector to one of the original vectors. A caricature is an exaggeration of features with respect to some mean.
Towards Average Dane (+1.7 Dane)

Towards Ajay (-2 Dane)

Morphing to Average Female Dane
Ajay
 Average Danish Female
Average Danish Female
 Cross Dissolve Only
Cross Dissolve Only
 Warp Only
Warp Only
 Warp and Cross Dissolve
Warp and Cross Dissolve



 Source B
Source B
 Midway Face
Midway Face









 Cross Dissolve Only
Cross Dissolve Only
 Warp Only
Warp Only
 Warp and Cross Dissolve
Warp and Cross Dissolve
