Overview

In this project, we computed a morph sequence of faces by first defining a set of points on two faces, then calculating the warp between both those faces and a median face, and finally warping at different proportions of each image and cross-dissolving between the result images for the sequence. We extrapolated this concept (the notion of faces as a vector of points), to calculate the mean face of a population, swap the gender of a face, and calculate caricatures by increasing the component of the face that is most different from the average image of a face.

Section I: Process of the Morph Sequence

Part 1: Defining Correspondences

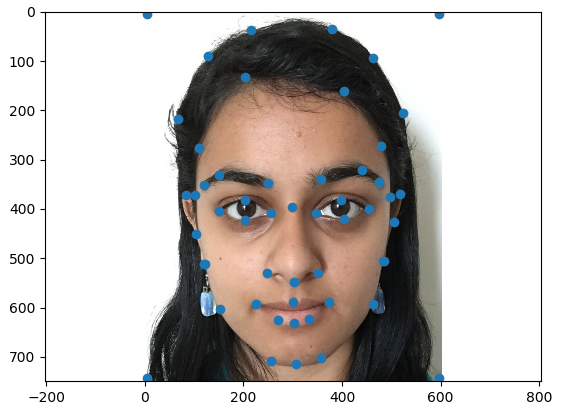
The first step to generating a morph is to define a correspondence between faces. I did this by manually selecting points according to a predescribed set of rules, as shown below. The inclusion of the four corners allowed me to think of the background as a set of triangles and therefore allow the algorithm to take care of transferring the background as well.

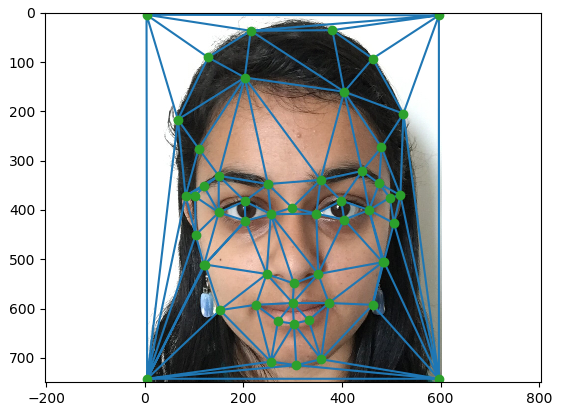
After this, we calculated a Delaunay triangulation between the points in this correspondence, as shown in the image on the right. This finds the triangles between the points that best represent the image, and returns them as a list of point numbers. It is important to keep the same triangulation between images, as these tirangles will be transformed into the corresponding triangles in the other image.

Part 2: Computing the Mid-Way Face

In order to compute the mid face between two images, I first found an average shape for the two images in points. Then I warped both source images A and B to follow the points of the average image and then finally use half of each image in the final. The two source images, those images warped to the midpoint, and the merged image, are shown below.

In order to make my algorithm run faster, I iterated through all the triangles in the image, found the masks corresponding to each triangle, warped each mask back to the position it would be in the source image, multiplied to find the corresponding pixels of the source image, and used those source points to fill in the triangle location in the mid-way face. I also kept track of the masks in order to make sure that if a point in the midway face is computed more than once, the value is divided by the appropriate number.

As a result of my vectorization, I can run an image in less than a second, and a sequence of 45 images (as described in the morph sequence below) takes about 30 seconds to compute. This made it very easy for me to run multiple sequences, and the main stopping point was choosing all the correspondence points on each image.

Part 3: The Morph Sequence

To implement the morph sequence, I simply ran the same algorithm as mid-way face, but with a different alpha constant for each step in the sequence. Varying the fraction of warp and dissolve uniformly between 0 and 1 made for a good sequence (in the midway face, these constants are both 1/2). Here are a few examples

(Note: this can be really trippy to look at, watch out) (Note: You may have to wait for some of these gifs to load).

Section II: Average Faces and Not-So-Average Faces

Part 4: The Mean Face

I calculated the mean face by first finding the average points of all the images in the category, then warping each image to the average, and finally averaging the pixels of all the images. The results are displayed below.

I also warped my face to the points of the average face and vice versa. The results were very interesting, as my face is markedly different from the average older Danish woman. I have learned from this project that my eyes are uncomfortably large when compared to average Danish women.

Part 5: Caricatures

I computed a caricature by subtracting my face's points from the average face, multiplying that difference by a caricature fraction (about 0.5), and then adding the points back in to the original image points and warping my face to fit those points. I have discovered from this that my observations above are correct, and that I do have very large eyes.

Section III: Bells and Whistles

Part 6: Gender Swap

As an extra idea, I experimented with modifying my perceived gender by subtracting the difference between the points on an average boy and and an average girl, and then multiplying that difference by a factor (about 0.3) and adding it in to my face's original points. The results can be seen below.

I also tried changing my race by warping my face to the standard coordinates of an average asian face. The results are shown below, and the warp factor I used was (0.5).

Part 7: PCA Basis

I calculated a PCA basis for this system by flattening every set of points in the image set into a 1 dimensional vector, stacking them, and calculating the PCA transformation. I tried one set keeping 30 components (since I only had 36 images, I couldn't get too much more precise), and another set using 10 components.

I then computed an average in the PCA basis and found that the returned points were remarkably similar. This is because I'm using the PCA basis on an image that is comprised entirely of information that the PCA basis has "seen before".

I also separated out one image (the first image) from the set, calculated the pca basis without it, and then caricatured that image. The results are shown below. You can start to see the difference in 1* warp. In the 2* warp, it's clear that with only 10 components, there wasn't enough variation maintained in the top left corner to morph his head inwards in the caricature, as is present in the 30 component image. We can see some information has been lost.

The results are not necessarily better than the original, but they do take less time to compute as you're computing in a lower dimensional space. Since my algorithm already runs pretty fast, (about 30 seconds for a 45 image warp sequence) this was not that noticeable.

Part 8: In-class Morph Chain!

We made a morph chain! In case the video embedding below doesn't work, here's the link:

https://www.youtube.com/watch?v=h-Oow96qhck&=&feature=youtu.be