Face Morphing
CS194-26 Fall 2018
Bernie Wang
Overview
In this project, we explore the concepts of image warping and data-driven methods on faces. The goal is to compute a "mid-way" image of two faces, create a gif of one face morphing into another face, demonstrate data-driven methods using a dataset of faces to extrapolate from the mean.
Defining Correspondences
In order to morph from one face to another, we need to annotate correspondence points for both images. We then compute the Delaunay triangulation on the correspondence points so that each part of the source face maps to the correct part of the target face. Here, I use my face as the source image and will morph it to Elon's face as the target image.

My face

Elon's face
Computing the "Mid-way Face"
To compute the mid-way face, we take the average between the correspondence points of the source image and target image to find the shape of the mid-way image. Then for each triangle in the Delaunay triangulation, we find the mapping from the mid-way to the source image, then find the pixels from the source image and transfer then onto the mid-way image given the affine transformation. This can be accomplished by calling morph(im1, im2, im1_pts, im2_pts, tri, warp_frac=.5, dissolve_fra=.5).

Bernie

Elon

Mid-way image
Morph Sequence
To get a morph sequence, we compute intermediate morped images by sweeping through the warp fraction and dissolve fraction from 0 to 1. Here, we computed 43 intermediate images along with the source image and target image to create a 30fps gif.

Bernie morphing into Elon
The "Mean face" of a population
In this section, we compute the mean face of a population from a subset of images from the IMM Face Database. In our case, we compute the mean face of images of Danish mean who are facing forwards. This is achieved by compute the average of the corresponding points, morphing each image to the mean shape, and cross-dissolving.

Mean face of Danish men facing forward
Morphing Faces to the Mean
Once we computed the mean face, we morphed each face in the subset into the mean shape

Image 01-2m, original

Image 32-1m, original

Image 40-2m, original

Image 01-2m, morphed

Image 32-1m, morphed

Image 40-2m, morphed
Morphing Mean Face to My Geometry
Here, we annotate the mean face and my own face to get their respective corresponding points, then morph the mean face into my geometry, and vice versa.

Mean face of Male Danes

Danes morphed into Bernie
Morphing My Face to Danes' Geometry

Bernie

Bernie morphed into Danes
Caricatures: Extrapolating from the Mean
Next, we compute caricatures of ourselves by adding a certain amount of our features to the mean face of a population. The result is a face with exaggerated personal features. We can also subtract our features from the mean, resulting in a face that is closer to the mean. To do this, we set a delta to be the difference between our own corresponding points and the corresponding points of the mean face. Then we multiply it by a scaling factor, which we can varying, and add it to the corresponding points of the mean face. Lastly, we morph our face to that shape characterized by the corresponding points of our caricature.
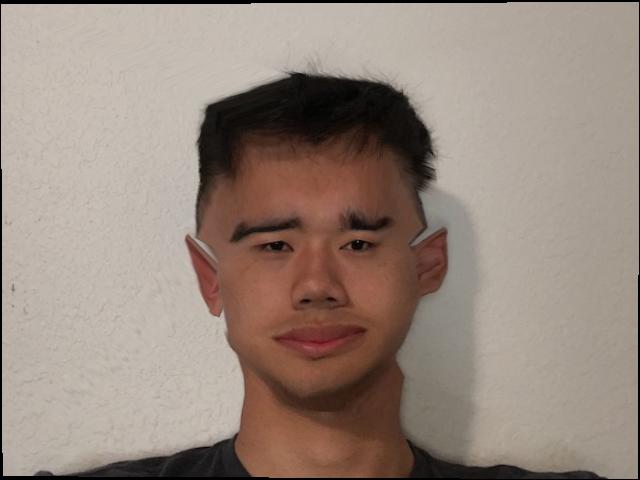
Scaling factor=-0.5
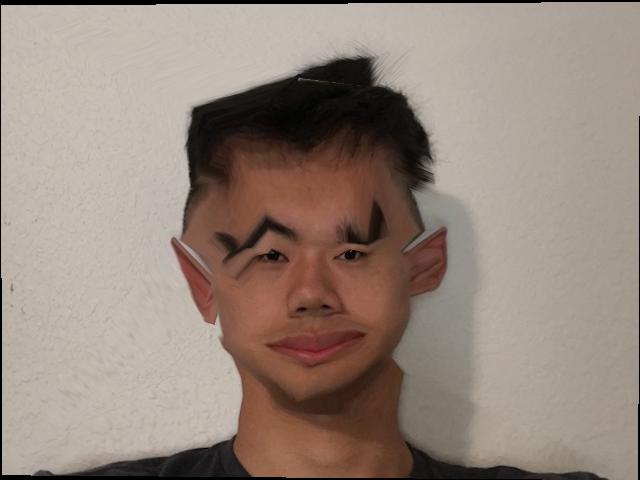
Scaling factor=-1

Scaling factor=1.5
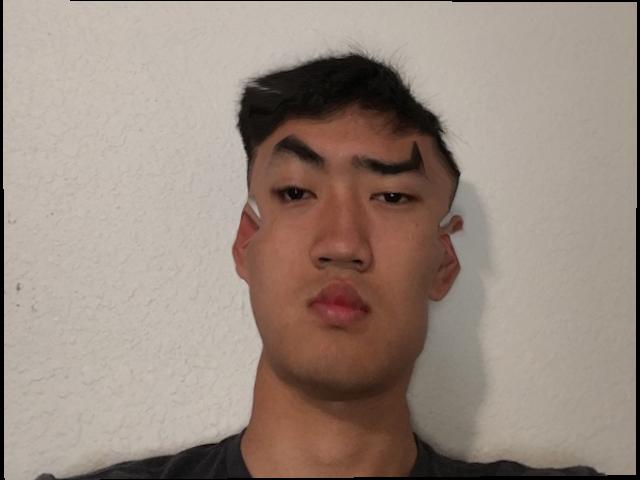
Scaling factor=2.0
Bells & Whistles: Changing my Ethnicity
We can change our ethnicity by computing an intermediate morph between our own image and a mean face of a specific ethnic group. In our case, we chose the mean of African-American males. Here's what it looks like when we morph my face to the mean's shape, compute the cross-dissolve of my face and the mean, and compute the mid-way image between my face and the mean face.

Average African-American male
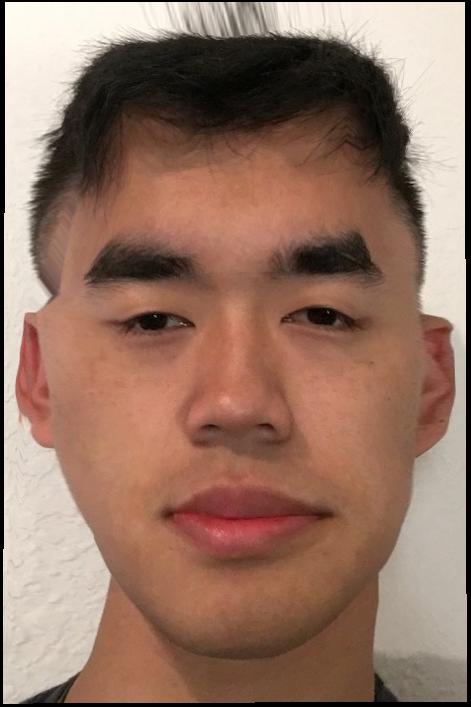
Bernie morphed to average African-American male

Bernie cross-dissolved with average African-American male

Mid-way image of Bernie and average African-American male