CS194-26 Project 6a

Warping

Given two images taken with the same center point but rotated, we can use homography matrices to implement a perspective transformation. Here is the algorithm for warping im1 to im2.

1. Define correspondence points for im1 and im2.
2. p' = H * p, such that p' are the correspondence points for im2 and p are those for im1. Define H using the following linear system of equations:
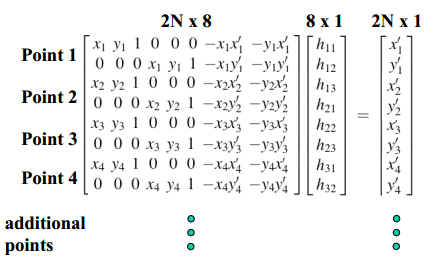
3. Compute the size of the warped image result by left multiplying the four corners of im1 with H. You might get negative coordinates, which means the warped image is translated beyond the size of the original image. To offset this translation, define a translation matrix T using the minimum x- and y-coordinates of the computed corners.
4. For each coordinate p in the warped image shape, retrieve the source point via inverse warping, with p' = inverse(T * H) * p. Sample the pixel value using interp2d for each color channel.

Results

Mosaics

After implementing the warping algorithm, we can produce a mosaic by warping one image im2 to reference image im1, keeping im1 unwarped. When we warped the four corners of im2 to calculate the output size, we also calculated the translation offset of this image relative to the reference image. By doing this, so we can simply stack the two images on top of each other to produce a mosaic.

Results