Overview
In this project, we aim to utilize image warping to implement image mosaicing. By calculating the homographies, we are able to combine images taken with overlapping fields of views views from the same point, but with the camera rotated to point at different angles, and stitch them into a single image utilizing projective morphing.Shoot the Pictrues
Recover Homographies
The homography transform follows the following equation where H is a 3x3 matrix, where i = 1 and thus has 8 degrees of freedom. x and y are the original point, whereas x' and y' are the point following the transformation. Thus, we recover the homography by attempting to find H in the following equation.
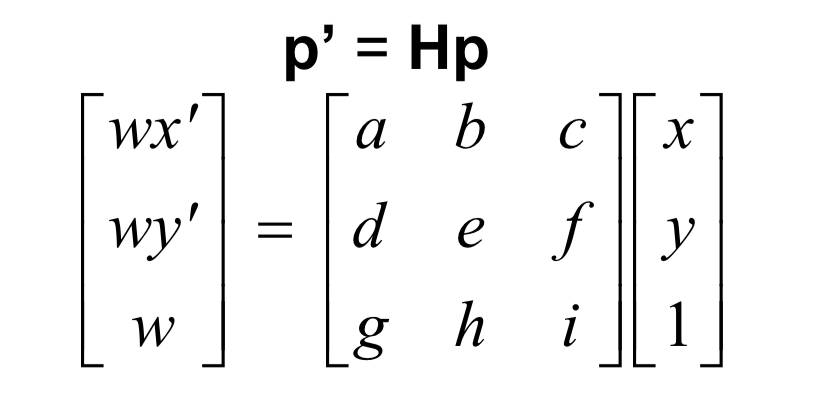

Image Rectification
Using the recovered homographies, we can warp the images to rectify the images. Warping the image is achieved by mapping the four corners of the original image through the homography transform to obtain the four corners of the result image and calculate the size. Then, for each pixel in the resulting image, we can calculate the pixel's value by using the inverse of the homography matrix to identify where we should sample the original image. Using interp2d, we are able to avoid aliasing the image and retrieve the pixel value for the position. To rectify planar images, I selected points with a known shape (i.e. windows and doors are rectangular) to generate the points the image should be warped to when generating the homography matrix H.
Doe
Wheeler
Doe Rectified
Wheeler Rectified
Blend into Mosaics
To blend two images together into a Mosaic, I computed a homography matrix to transform the points selected from the left image (im1) to the corresponding point coordinates selected from the right image (im2). We can then use the inverse homography transform similar to our image rectification to compute a warped version of image 1. To combine the two images together, using element-wise maximum over the pixels from each image for overlapping regions produced a fairly seamless blend without introducing unnecessary blurring that can result from alpha-blending.
Doe 1
Doe 2
Doe Merged
Wheeler 1
Wheeler 2
Wheeler Merged
Steps 1
Steps 2
Steps Merged
Summary
From this project, I learned the importance of linear algebra and how relatively simple systems of linear equations can yield powerful transformations that can alter images and perception.