Shooting The Pictures, Recovering Homographies
As the project mentions, it's best to take photos that have a lot of overlap. It's also to important to take images that simply rotate the center of projection, so that outer images aren't heavily warped.
I used ginput for users to define common points. Attached below is the user interface that users can define the points needed. Users would click a point in the left image, then click the corresponding point in the right image.
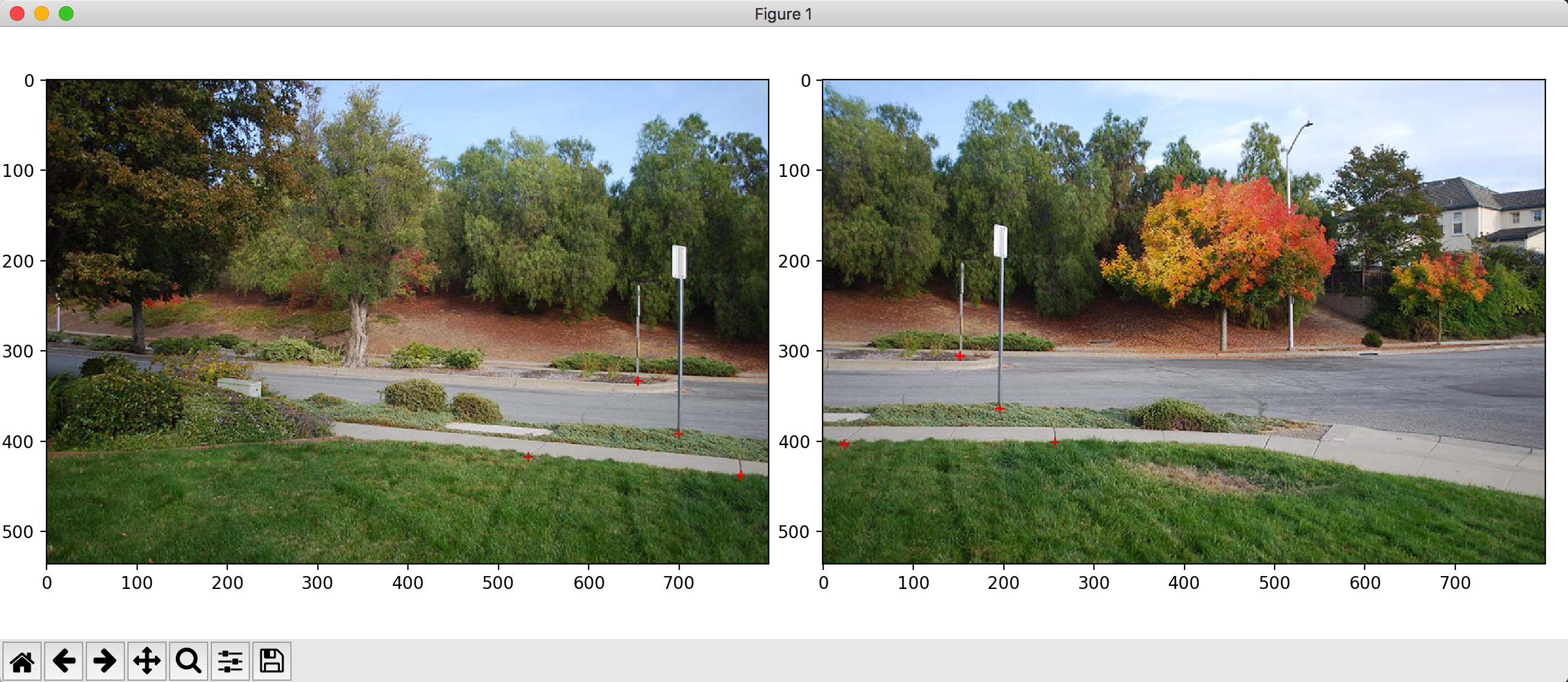
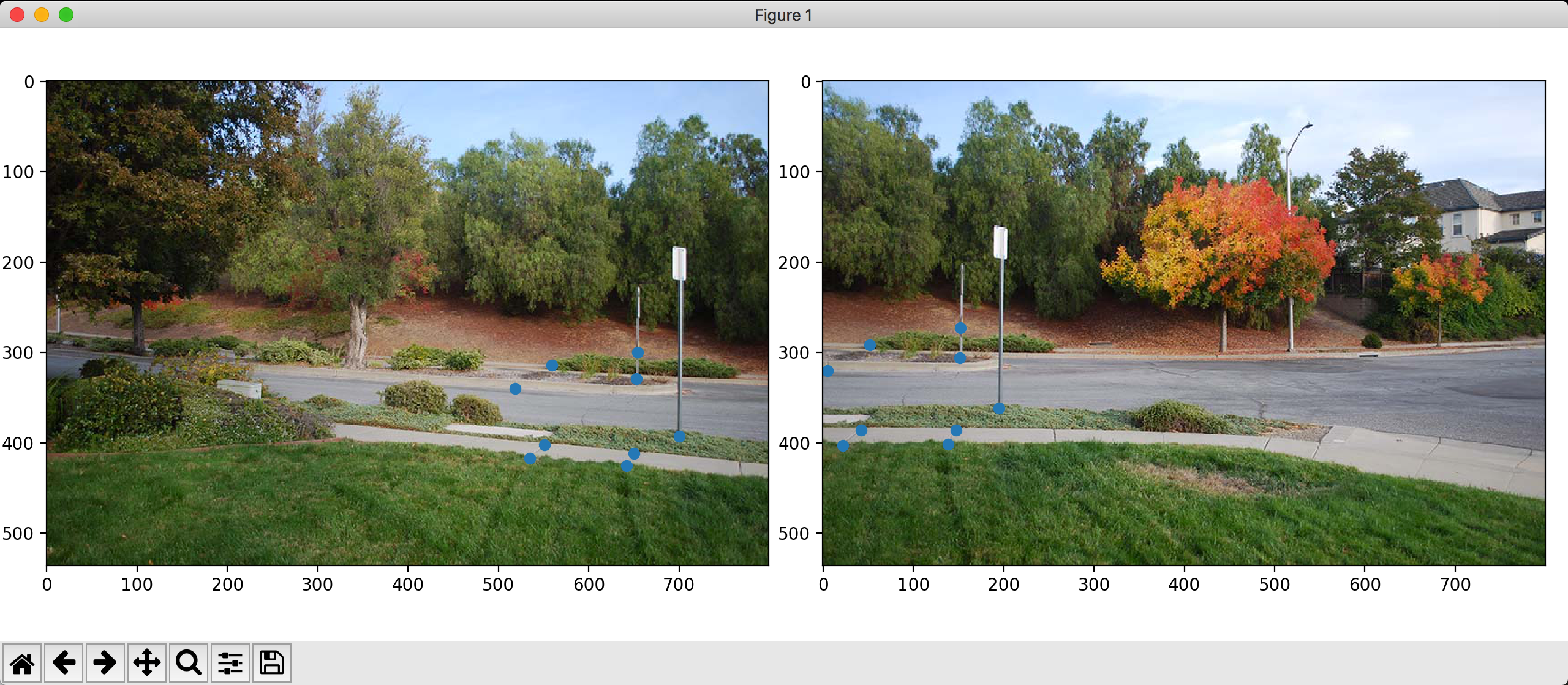
Below are the points for the example warps. Notice how the points are at corners, and line up between the images.

Warping Images (and Rectifying them)
Using the points defined above, we can use least squares to compute a good matrix to compute a projective transformation of the points.
To do this, I set up a matrix to determine what the 8 unknown value of the H matrix were–we use least squares so that we can use the data from more than 4 correspondences, and so that we're resistant to error.
Below are two examples of warped images for panoramas


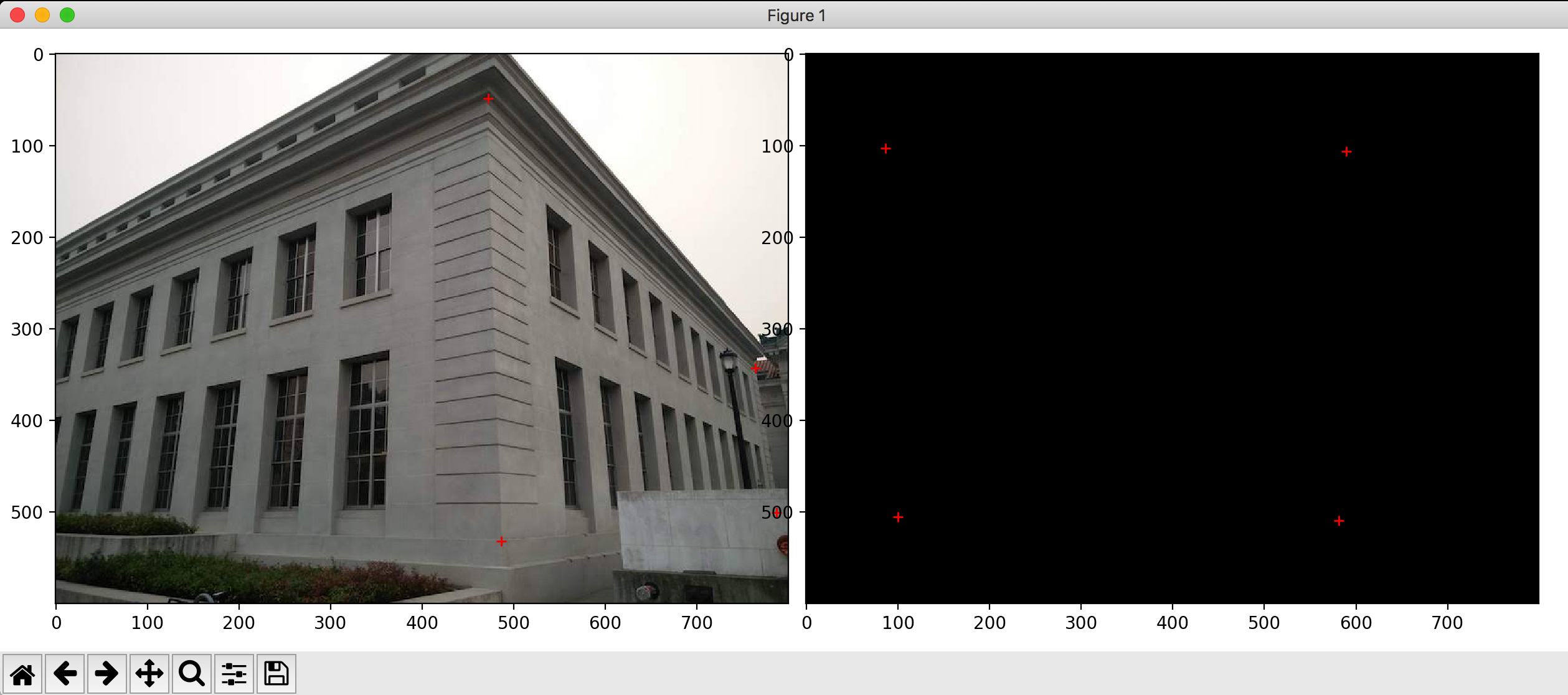
We can also use this method to "rectify" images. This includes transforming images of the sides of buildings to make it look like the photo was taken edge-on.
Below you can see some examples of the images as well as the GUI built for the warping. Note: the recified images are cropped portions of the full image.




Stitching and Blending Panoramas
Bringing everything together
Time to stitch the images together! I took the approach to add the images together, blend the overlap, and then warp the combined image to the third image's points. I did linear alpha blending to blend.
Overall strategy: image -> warp -> add next image and blend -> warp -> add next image and blend
For blending, I calculated where the overlap between the two images started to happen, then I progressively increased alpha for the new image, and decreased alpha to 0 for the warped image.
Below you can see the original images, and the final panorama.














