Image Warping and Mosaicing
CS194-26 Fall 2018
Andrew Campbell, cs194-26-adf

Introduction
A panorama is a wide-angle view of a space. The most common method for producing panoramic images is to take a series of pictures with slightly overlapping fields of view and stitch them together. To avoid parallax, the camera should be rotated about the center of its lens.
There are three main projection modes used in stiching images: spherical, cylindrical, and perspective. Spherical projection tries to align and transform the photos as if they were all plastered onto the inside of a sphere; it works well for 360 panoramas. Cylindrical projection projects the panorama as if it were placed on the inside of a cylinder; it works well for very wide panoramas and is used by most smartphone apps. Lastly, perspective projection projects the panorama as though it were mapped on a flat surface. In this mode, straight lines are kept straight, but excessive distortion may occur at the edges for wide panoramas. In this project, we will focus on perspective projections.
Specifically, we will take as input three photos with the same point of view but with rotated viewing directions and with overlapping fields of view. Then we will use point correspondences to recover homographies from the left and center images and center and right images. We then perform a projective warp on the left and right images. Finally, we blend them together to create a panorama.
Recovering Homographies
Any two images of the same planar surface in space are related by a homography. The 3 x 3 homography matrix has the following form:
It has eight degrees of freedom (as the last entry is fixed to be 1) and thus in principle only requires four point correspondence pairs to be recovered. However, this approach is prone to noise and in practice we find least square regression on many pairs of points works better. Given pairs of points for the first image and second image , we wish to find such that
is minimized. It can be shown through some algebra that the relevant matrix equation is
We can solve for using least squares to recover .
To obtain point correspondences, we manually record coordinates of the same features in both images. This is a tedious task; we will automate the process in the next part. I found that using 20 point correspondences was sufficient.
Image Rectification
We can now perform (inverse) image warping: for every coordinate value in the output result, multiply by the (inverse) homography matrix, taking care to normalize to be , to recover the “lookup” coordinates in the original image. We perform interpolation to avoid aliasing.
One application of a homography is image rectification: given an image containing a planar surface, warp it so that it is frontal-parallel. We simply select 4 points representing the corners of the plane in the original image and choose the correponding points in the output to be the corners of a rectangle. Below we illustrate some examples.




Mosaics
Given three images with the same point of view but with rotated viewing angles and overlapping fields of view, we can create a mosaic. We can recover the homography transformation as detailed above, and warp the left and right images appropriately. Note that in order to capture all of the warped result, we first create a large blank canvas and place the image in the center.
In order to blend the resulting warps, we can simply use alpha blending by multiplying the image by a feathered mask. Some example masks for the left, center, and right images, respectively, are shown below.
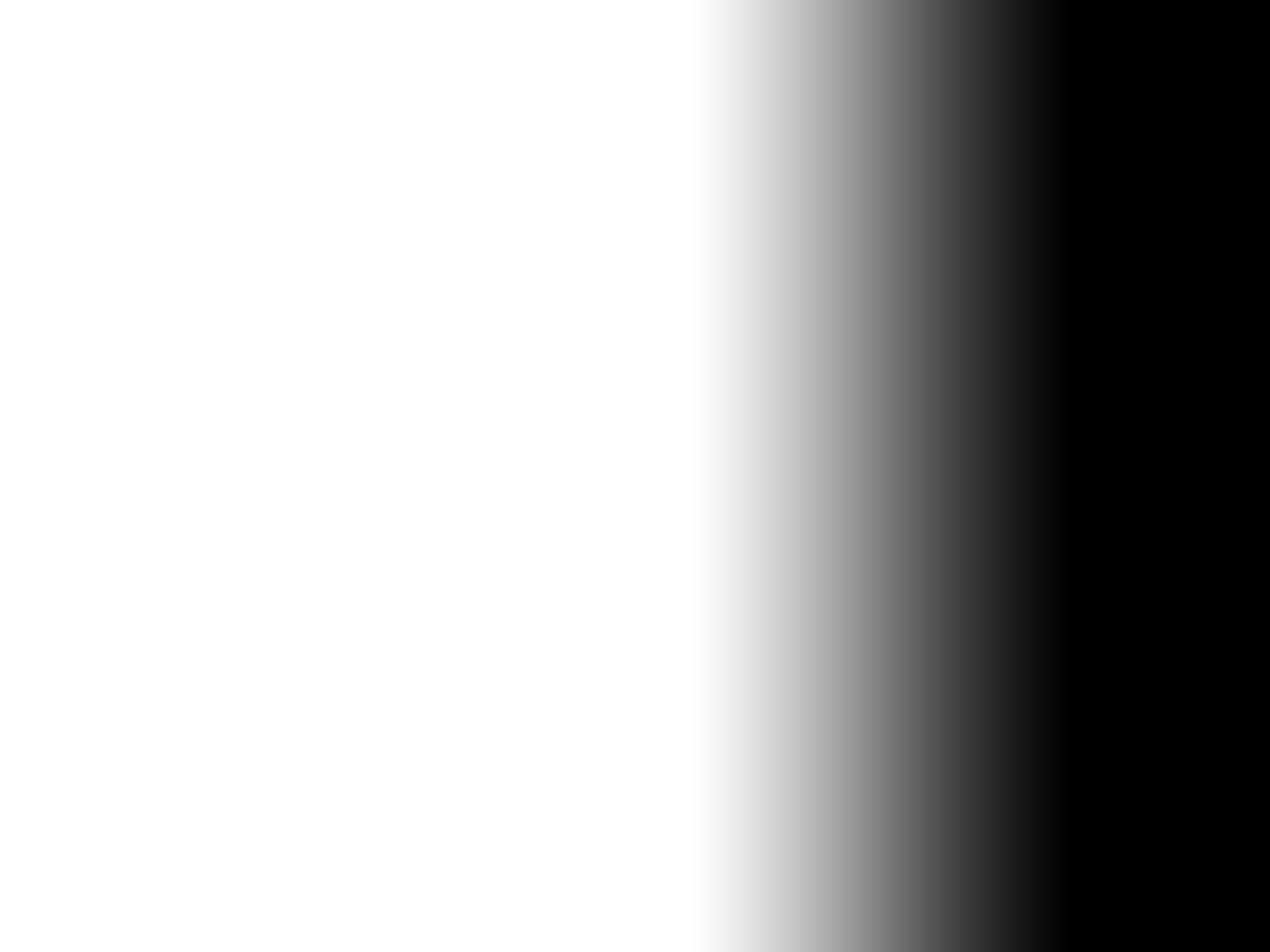


Results




























What I learned
Linear algebra is powerful; manual correspondence picking is tedious; and panoramas are cool.