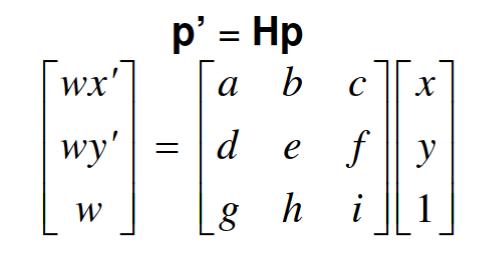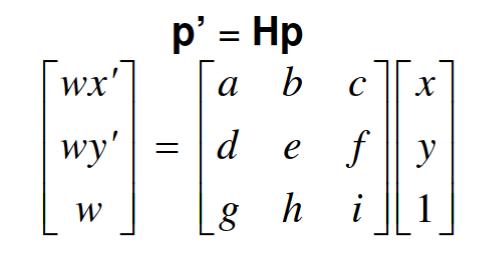CS 194-26: Image Manipulation and Computational Photography

Project 6-1: Image Warping and Mosaicing

Tony Pan, CS194-26-adn

Overview

This project focused on image warping and mosaicing. This involves defining point correspondences on one or more images, calculating the homographies between these points, and warping (and or blending) to achieve a result image.

Part I: Recovering Homographies

This part involved calculating the homography H that allows us to map between different projections. In this case, using the equation below, we are able to create a series of equations that can be then solved using least-squares (provided more than 4 correspondences are given). The solution to the least-squares problem are the values a through h of the homography, with i being 1.

Part II: Image Warping & Rectification

Given the homography, it becomes relatively simple to warp or rectify an image. The process involves resampling the image using an inverse warp, such that values in the warped image are interpolated from the original. This process allows for some pretty interesting effects, such as warping such that a certain plane is front-parallel. The images on the left are before the warp is applied, and the right set of images shows the effects of rectification. As can be seen, both images have some planar surface that has been warped to be front-parallel.

Part III: Image Mosaicing

Image mosaicing operates similarly to image warping, only in this case two images are warped to some central correspondence and joined. Defining matching correspondences was pretty hard using ginput, but I ended up getting some good results without having to pixel-match too hard.

In the above mosaic, I had some trouble getting everything to match up, and there are still some artifacts visibile after laplacian blending. For instance the gray sedan in front of the house has some noticeable artifacts near its bumper area. Though it may be possible to achieve a better blend with better correspondences, this was the best result I got on that set of images. All in all, I think that this method of creating mosaics works quite well, so long as you are able to define correspondences that match each other closely.