Part 1.1 - Finite Difference Operator
To compute the gradient magnitude image, I calculate the square of the images convolved with Dx and Dy, sum them up and take the square root of it. The threshold for edge image is 0.19. All pixels with value larger than the threshold is converted to 1, whereas others converted to 0.

Convolved with Dx

Convolved with Dy

Gradient Image

Edge Image
Part 1.2 - Derivative of Gaussian (DoG) Filter
Method 1: Blur the image using Gaussian Filter, before applying Dx, Dy operators.
Threshold for edge binarization: 0.05
Gaussian kernel parameters: ksize = 9, sigma = 2
Compared with the results I got in part 1.1, the edges here are amplified. It's clearer to see the edges as shown in the finalized edge image.

Gaussian Blurred Image

then convolved with Dx

convolved with Dy

Gradient Image

Finalized Edge Image
Method 2: Convolve the gaussian Filter with Dx and Dy, then apply the convolved filters to the image.

A. Gaussian convolved with Dx/p>

B. Gaussian convolved with Dy

C. Image convolved with A

D. Image convolved with B

E. Gradient Image of C and D

F. Finalized Edge Image
As illustrated from the images above, method 1 and method 2 yield the same results.
Part 1.3 - Image Straightening
The Gaussian filter used in this case has a size of 9 and a sigma of 2.

Straightened "facade.jpg"
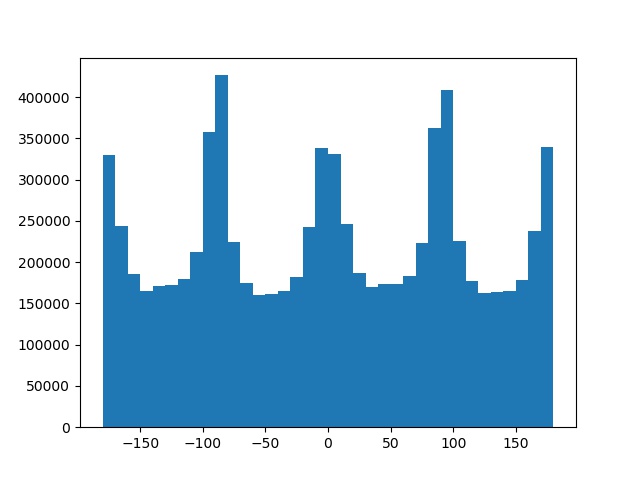
Histogram of Gradient Angles
- More Examples -
Below are the results of the algorithm run on other examples.

"window.jpg"

Straightened
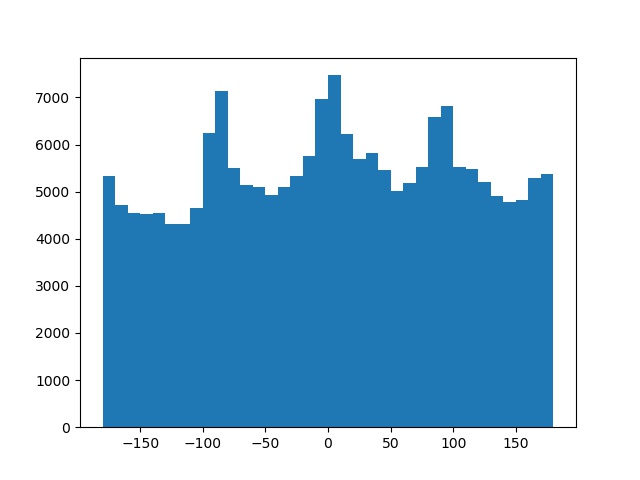
Angles

"vine.jpg"

Straightened
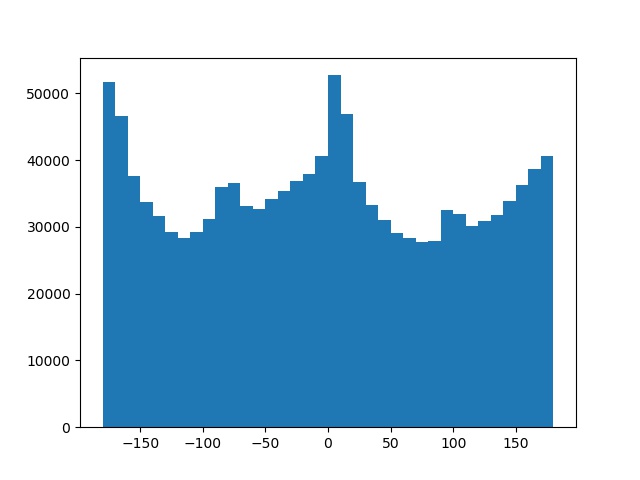
Angles
- Failure Case -
I have also included a failure case of this algorithm. It not only failed at straightening the face, but further tilted it towards the wrong direction. My speculation of the reason behind this is that human face has no straight lines or perpendicular angles, therefore there is nothing for the algorithm to work with in the image.

"face.jpg"

Straightened
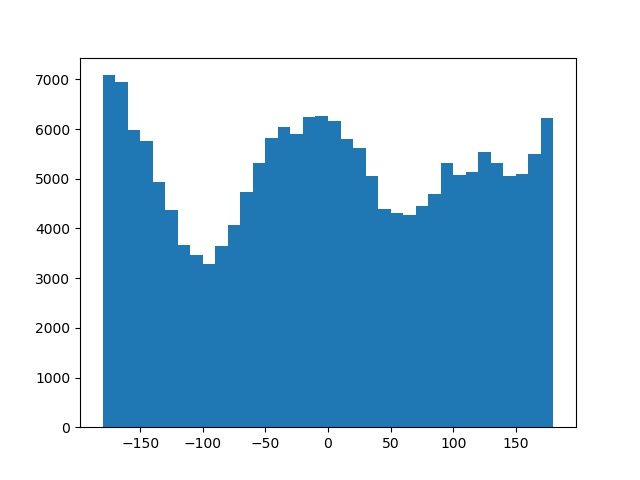
Angles
Part 2.1 - Image "Sharpening"
- Step by Step -
My first attempt at sharpening the image is a step by step approach. I used Gaussian Filter to blur the image, subtract it from the original image to get the high frequency portion. Then I added the high frequency portion (amplified by alpha) to the original image, getting a sharpened version. In summary: Sharpened Image = Original Image + alpha * (Original Image - Blurred Image).
"taj.jpg", Gaussian Filter (ksize = 9, sigma = 1), alpha = 3

Original Image

Gaussian Blurred Image

High Frequency

Sharpened Image
"helsinki.jpg", Gaussian Filter (ksize = 9, sigma = 5), alpha = 4

Original Image

Gaussian Blurred Image

High Frequency

Sharpened Image
- Unsharp Filter -
The above process is equivalent as constructing an unsharp filter and applying it to the image. Unsharp Filter = (1+alpha) * Unit Impulse Filter - alpha * Low Pass Filter

"taj.jpg"

Sharpened using Unsharp Filter

"helsinki.jpg"

Sharpened using Unsharp Filter
Other examples.

"london.jpg"

Sharpened

"tokyo.jpg"

Sharpened
For experiment, I blurred an image and tried to sharpen it again. However, the high frequencies are lost in the process, and the resharpened image is not the same as the original image.

"paris.jpg"

Blurred "paris.jpg"

Resharpened "paris.jpg"
Part 2.2 - Hybrid Images
Below are a few examples of the hybrid image results I generated using the described method.

"DerekPicture.jpg"

"nutmeg.jpg"

Hybrid

"dog.jpg"

"kitten.jpg"

Hybrid

"hulk.jpg"

"cat.jpg"

Hybrid
There are also failure cases. For example, the image below is a terrible hybrid because the figures in original images have completely different postures that are barely overlapping when images are aligned. The combined result is not optimal.

"dog.jpg"

"kitten.jpg"

Hybrid
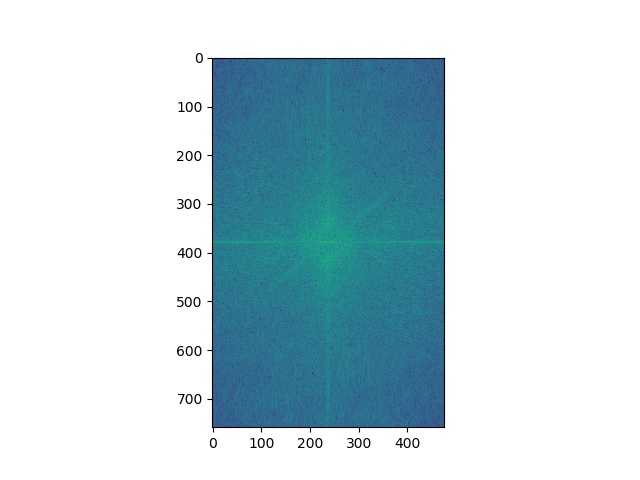
Example 3 and the corresponding log magnitude of the Fourier transform are shown below. At first, the high frequency portion is too dim that even at a small distance, I can hardly see its shape. I intended to blur the low frequency portion harder and amplify the high frequency portion. After a few experiments, I am satisfied with the results I get at sigma(low-freq) = 13, sigma(high-freq) = 15 with a Gaussian filter size(ksize) of 15.




"madhatter.jpg"
"harley.jpg"
Low-Freq Portion
High-Freq Portion
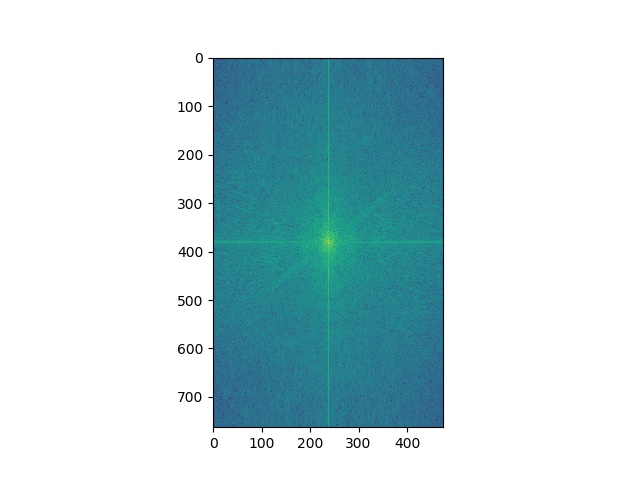
Hybrid
Part 2.3 - Gaussian and Laplacian Stacks
Gaussian Stack, N = 5

level = 0

level = 1

level = 2

level = 3

level = 4
Laplacian Stack, N = 5

level = 0

level = 1

level = 2

level = 3

level = 4
Generate Gaussian and Laplacian stacks of the hybrid image "Hulk.jpg" + "cat.jpg", using N = 5 and a Gaussian Kernel of size 9 and sigma 5.
Laplacian Stack, N = 5

level = 0

level = 1

level = 2

level = 3

level = 4
Laplacian Stack, N = 5

level = 0

level = 1

level = 2

level = 3

level = 4
Part 2.4 - Multiresolution Blending
To create a blend of image A and B, I first built a mask (of only 0s and 1s), and computed the mask's Gaussian Stack. Then I constructed the laplacian stacks of images A and B. The blend of images is created by combining the results of their respective laplacian stacks according to weights given by the Gaussian stacks of the mask.
The oraple is constructed using a horizontal regular mask, with 1s on the left and 0s on the right.
N = 20, Gaussian stack: ksize = 10, sigma = 30, Laplacian stack: ksize = 30, sigma = 30.

"apple.jpeg"

"orange.jpeg"

Regular Mask

oraple!
The starry night blend is created using a vertical regular mask, with 1s on the bottom and 0s on the top. Of course, before the blending process, I had resized the two images to the same size.
N = 20, Gaussian stack: ksize = 10, sigma = 30, Laplacian stack: ksize = 30, sigma = 30.

"night.jpg"

"sky.jpg"

Regular Mask

A Starry Night
To blend the eye and the nebula image, I created an irregular mask of the shape of a circle. In preparation, I wrote some extra image-align helper functions that helped me aligned both the mask and the nebula image to the eye image, so that all three of them 1. have the same image size 2. the area to be blended are at the same location of each image.
N = 20, Gaussian stack: ksize = 10, sigma = 30, Laplacian stack: ksize = 30, sigma = 30.

"eye.jpg"

"nebula.jpg"

Irregular Mask (circle)
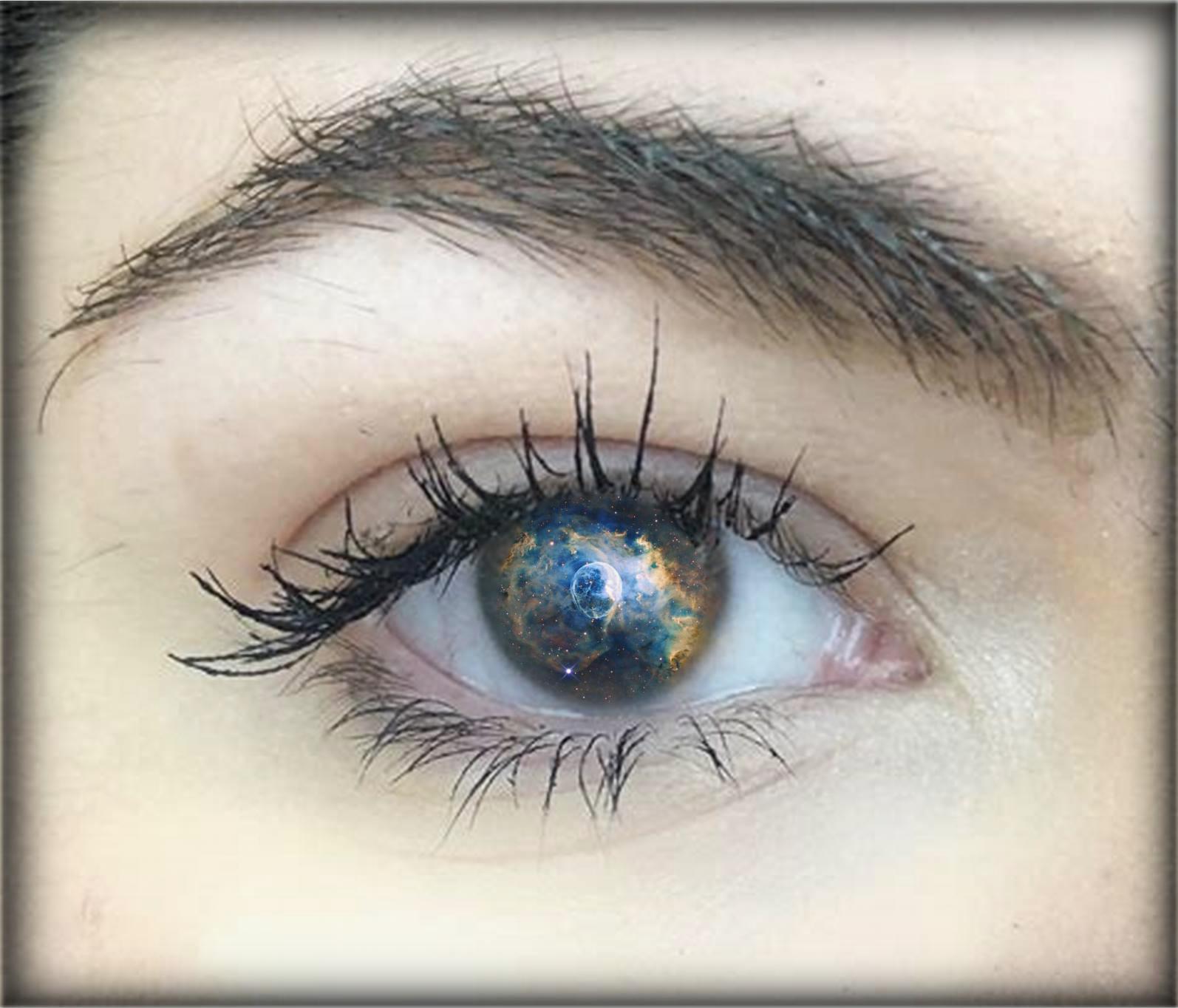
Nebula in the Eye
The full laplacian stack of blending the two images according to gaussian pyramids: "night.jpg" + "sky.jpg"



















