In this project the objective is to morph the face of person A into person B. Note that this is not a simple alignment + cross-dissolve but rather a careful and gradual transformation of the shape and color of person A's face into the shape and color of person B's face.
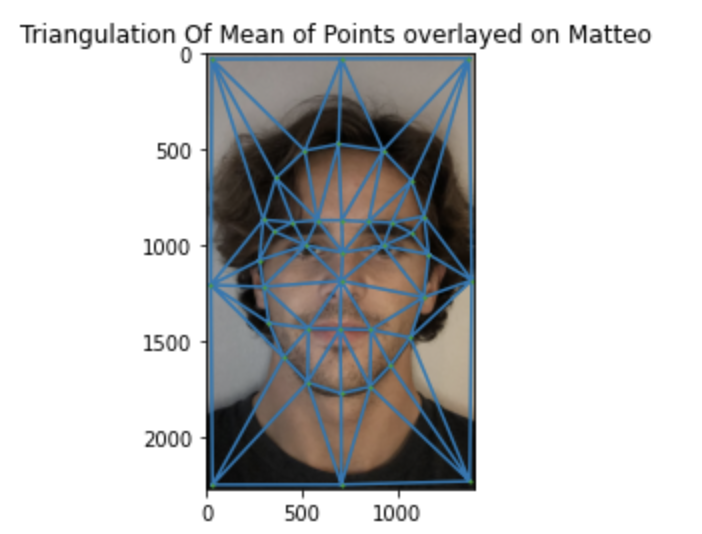
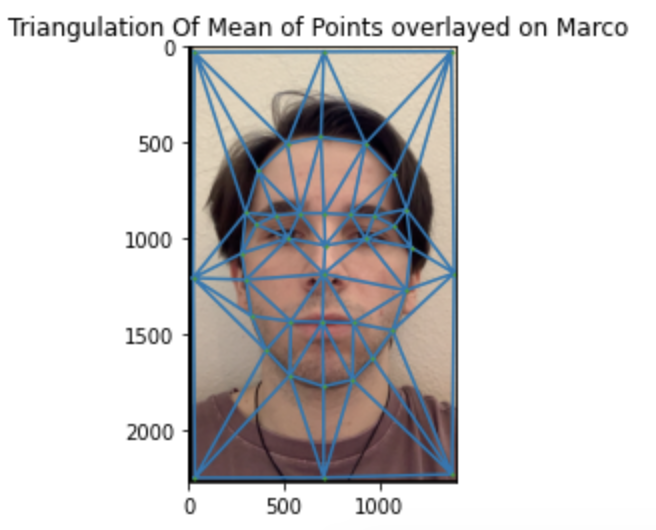
This is perhaphs the most important part of our morphing algorithm. In order to correctly change shapes we need to define a set of corresponding points in both images. To do this I manually went through both images and annotated a set of points that I believed captured relevant features and shapes of a person's face. I believe that for the morphing of my face into my brother's face I used 40 points.
Once the points have been established I used a Delaunay triangulation to create triangles from the computed correspondence points. This is important because the triangles determine the shapes of the faces. As a consequence, at each step of the morphing for a given warp fraction I compute a weighted combination of the two sets of points and then compute the traungulation of those sets of points. For example, for the midway face the weighted combination is simply the average. Here is the average triangulation overlayed on mine and my brother's face:

For simplicity, here are the original pictures I used for this project:


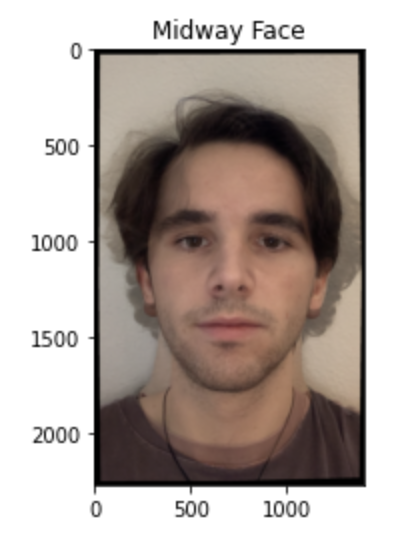
In this section the goal is to compute the midway face, i.e. the face that has average shape between my brother and me and is "averagely" cross-dissolved. The big question however is how do we go from the average shape (computed in the previous part) to the midway face?
Well, from the previous parts we basically have a goal shape, the average triangles can be thought of our target shape for this part of the project. Therefore, what we want to do is map the triangles in both images to the triangles in the average shape annd then fill in those pixels with the values from the original images. Since the forward map can leave holes (eg. imagine pixel with coordinate (2,2) in my image maps to pixel (2.3, 2.8) in the midway face image, where would you place the value from pixels @ (2,2)?) we actually compute the transformation matrix that takes us from the midway shape triangles to our own triangles! This way every pixel in the midway shape has its value taken from somewhere in the original images, thus leaving no holes. Now, you may be wondering, the same "anomaly" can occur. Some pixel with integer coordinates could map to a pixel in teh original images with decimal coordinates, what do we do then? Simple! We can think of the original image as a function, f: R^2 -> R, and then interpolate to obtain a continuous surface from which we sample at a given pair (x,y) to obtain the pixel value. This turned out to work pretty well, and is relatively fast. Another alternative is to simply round the decimal coordinates, which amounts to a nearest neighbor interpolation, this also worked well but I noticed that sometimes it would not be as smooth as the bilinear interpolation and it was also slower since the interpolation is simply computed once and then we have a function we can simply call to give us the pixel value.
The last question that remains un-answered is, how do we find this map that takes us from the average shape coordinates to our original coordinates? Well, this turns out to be a very basic linear algebra problem in which we want to perform a change of basis. In our home space the vertices of a triangle have a specific set of coordinates, which we can imagine all being at the same "height" of 1. We can arrange these in a matrix, let's call it A, in which the first row contains the x coordinates, the second row contains the y coordinates, and the third row contains the z. Our goal is to then find a matrix T such that TA = B, where B is the same matrix as A except the rows are now the coordinates of the same vertices in the average shape space. Since we actually want the inverse matrix, to handle the holes explained earlier, T^{-1} = (BA^{-1})^{-1} = AB^{-1}. We can then obtain all the points inside the triangle, using polygon for example, and apply this transformation in parallel to all the points by stacking them in a matrix.
In synthesis, the process is: Given a coefficient, compute the weighted combiantion of the points to obtain the target geometry, then for each triangle; compute the transformation matrix and apply it to all the points in the interior of it, fill these points in the new image with the points that you obtained in the previous step from the two images (obviously weighting the pixel values accordingly by the coefficient).
Here is the midway face, as well as my face with the midway face geometry, and my brother's face with the midway face geometry.


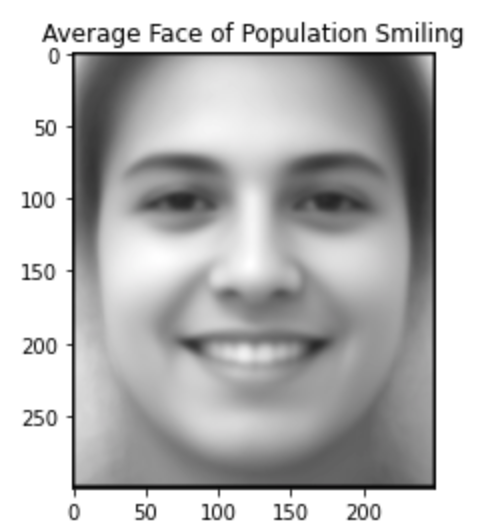
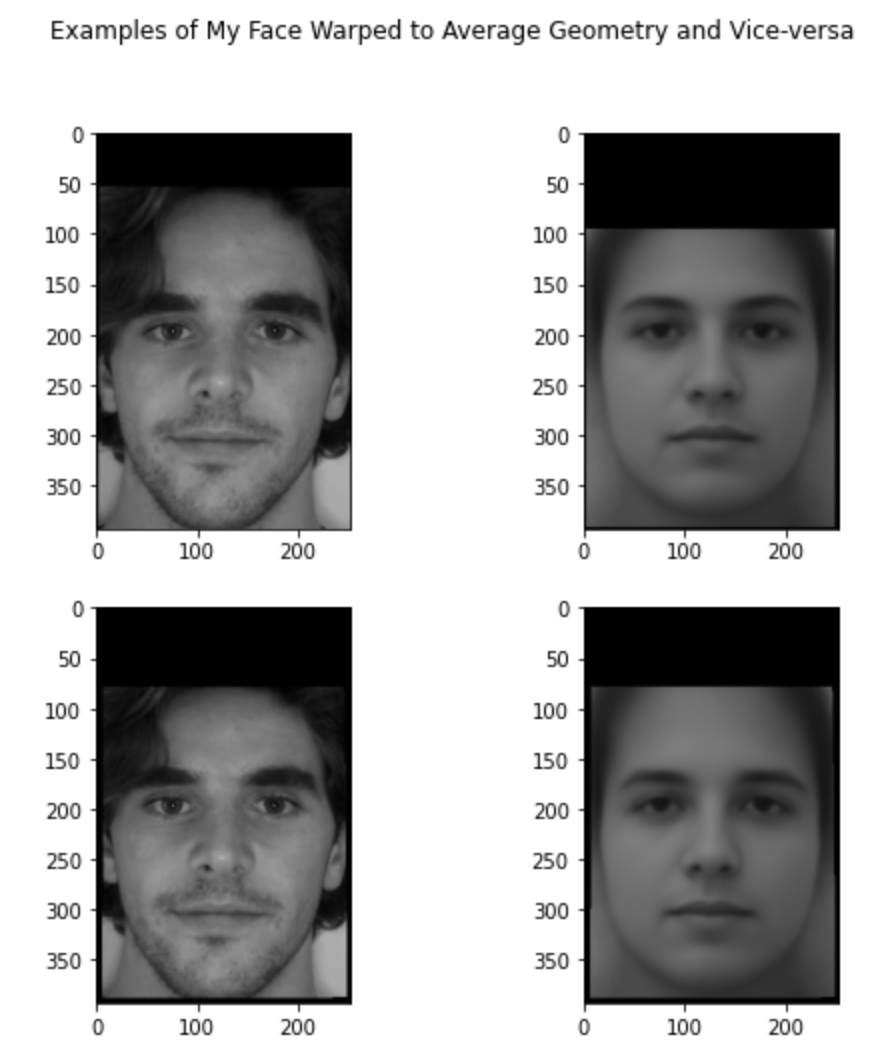
For this part I picked one of the freely available datasets of faces that have been manually annotated with the key feature points. The goal is to consider the average set of points from this database to come up with the average geometry of the population. Once we have the average points we can computer the average geometry by simply using a delaunay triangulation on these sets of points. To obtain the actual image I then morph all the images to the mean geometry and add them up. This is very similar to the midway face except it is the midway face between all the the faces in the dataset. Here are my results:

I then proceeded to morph all the faces in the dataset to the average shape. Here are a couple of examples I thought were funny, the top row is the original image and the bottom row is the image warped to the average geometry.

Finally, I also mrophed myself to the average face, i.e. what would I look like if my face was the average shape, and I also morphed the average face to myself. You can notice that the mean face morphed to my shape looks more masculine, morphing myself to the mean face resulted in subtle changes but I think you can notice my forehead changed and my eyes and eyebrows changed.
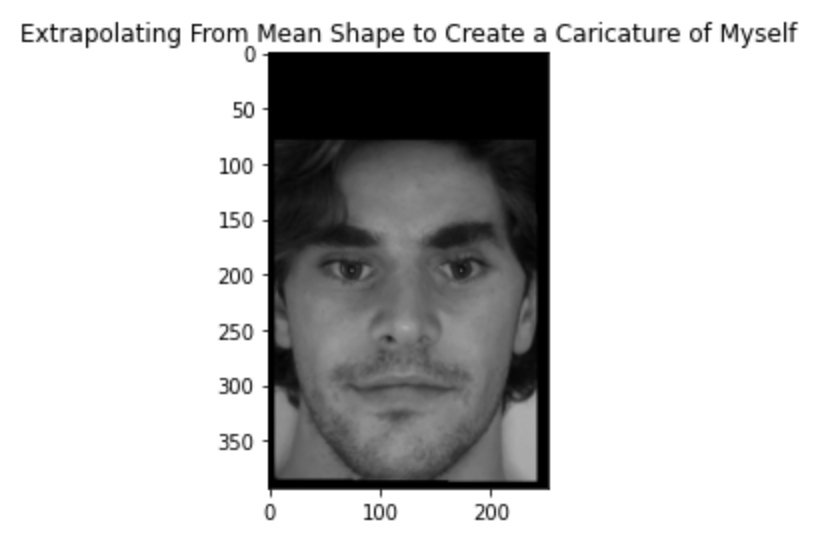
To produce a caricature of myself I used the average points and then extrapolated from those by computing a new set of points, caricature points. Mathematically caricature points = (1 + c)*averge_points - c*my points. This gave a pretty cool result, here is an example using c = 0.5 and 2, respectively:

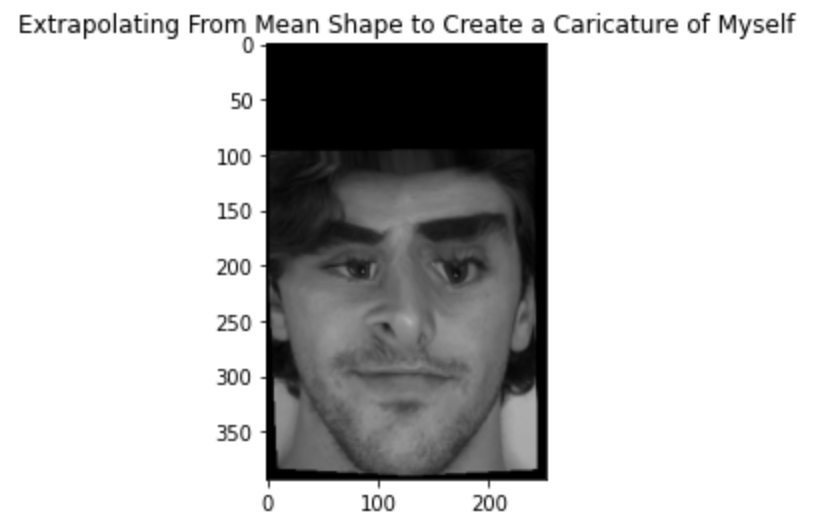
I also decided to try a different method which gave cool/funny results so I will include it here. I computed the standard deviation of the x and y coordinates of the average points. I then proceeded to add a fraction of the standard deviation to each coordinate, however the fraction was computed by sampling independntly from a gaussian distribution with mean 0 and variance 0.1. The result was really funny:
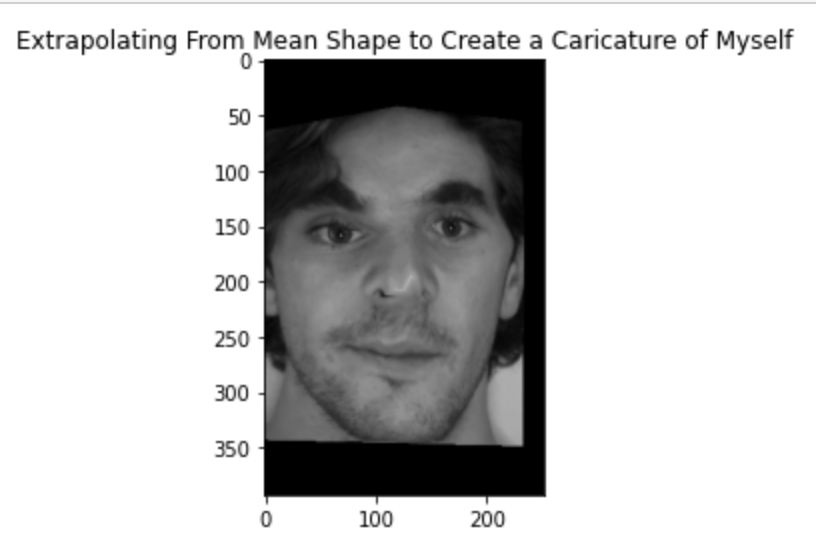
I then tried sampling from different gaussian based on x and y coordinate, the fraction of the standard deviation that was added to each point for the x coordinate was sampled from N(-0.1, 0.08) and for the y it was sampled from N(-0.5, 0.06). Keep in mind the standard deviation of the original points was huge since poitns are spread all over the image, therefore a small fraction still results in a noticeable change because the std was relatively large. Here is the result:
At this point the reader should be familiar with the star of my project, my girlfriend's dog Bane. Bane is a 1 year old shepherd husky mix and for the bells and whistles portion I decided to create a morphing video showing how Bane grew in the past year. The video, with a little music added to it, can be found here. I found it hard to select the right points because Bane's face actually changed a lot over the course of the year and her ears went from floppy to up right. I tried mapping the tip of the floppy ear to the tip of the straight ear but I saw that it resulted in a less smooth transition than if I mapped the mid of the floppy ear to the mid of the straight ear. Here is the video.