Project 3¶
Yiwen Chen
1.1 Defining Correspondences¶
In this section, I defined 43 pairs of correspondences manually using ginput. Then I computed Delaunay triangulation with the average of each pair.
Original images:


Annotated images:
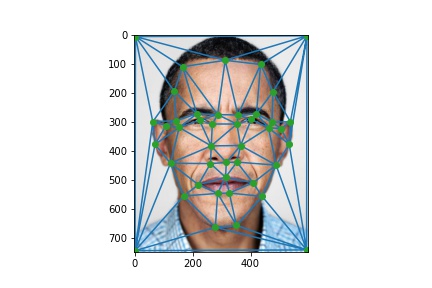
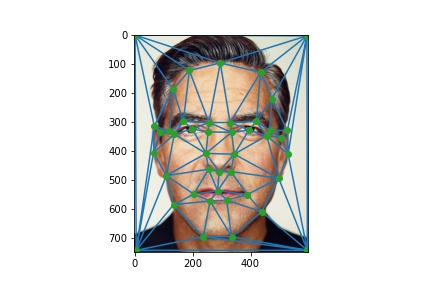
1.2 Computing the "Mid-way Face"¶
The following mid-way face is computed by
- Computing the average geometry by taking average of each corresponding pairs
- Computing affine transformation for each triangle from one of the original image to the mid way image. Use the inverse transformation to colorize points in the mid-way image.

1.3 The Morph Sequence¶
Similar to how the mid way image is constructed, for each a = 0.1, 0.2, 0.3, .. 0.9 a frame is constructed using a as both warp fraction (shape) and dissolve fraction (color).

2.1 The "Mean face" of a population¶
I used 6 ”happy” expression female faces from the Danes dataset. The original images are as follows:



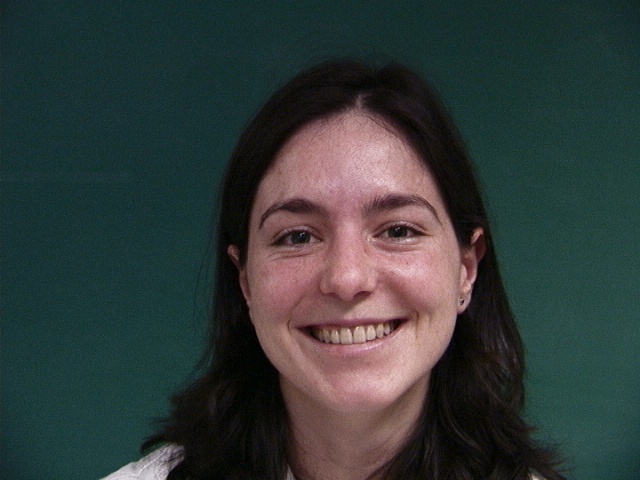


To compute the mean face,
- Compute the average face shape by taking average of all corresponging points given to us
- Morph each of the faces in the dataset into the average shape.
- Take average of all morphed face
Here is an example of step2
original:

morphed image:

The average face of ”happy” expression female faces:

2.1 From portrait to average and the other way around¶
Here is my original portrait:

The result of my face warped into the average geometry:

The result of the average face warped into your geometry:

2.2 Caricatures: Extrapolating from the mean¶
A caricature of my face is calculated by weighing my face with 1.5 and weighing the averge face with -0.5 for both shape and color:
