Report

Part 1: Defining Correspondences

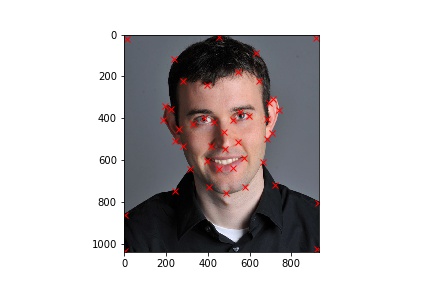
For this part, we use ginput in order to manually select points. Here, we need to match up the points on each image to ensure the triangulation is correct and not off.

Part 2: Finding the Mid-way face

To find the midway face, we take a few steps. We first get the correspondences for each image, and compute the average correspondences between the set. We then compute the Delaunay triangulation for this average shape. For every triangle in this triangulation, we compute a triangular mask which contains the coordinates of all points within the triangle. We then also compute the affine transformation matrix for the input's triangle and the average's triangle, and apply an inverse warp on the triangular mask using this matrix. We use RectBivariate to interpolate the missing points. We repeat this for every triangle and fill in a resulting image. We also do this for both images, and then cross-dissolve the two.

Part 3: Morphing

To create a gif of a morphing image, we use the same algorithm to compute the mid-way morph, but generalize it to use different alphas. In the example below, we use 40 frames.

Part 4: The "Mean face" of a population

To compute the mean face in a large population set, we first retrieve images with their corresponding correspondence points. Using these points, we calculate the average correspondences and then compute the Delaunay triangulation from this. We then warp every image to match this shape using a similar method as morphing, but without the cross dissolving. After all the images are warped, we add the images together and divide by the number of images to take an average.

Part 5: Extrapolating the Mean

To extrapolate the mean and create caricatures, we essentually use the same morph algorithm but instead use an alpha value greater than 1. We use a self portrait and use the average face we computed in the previous part, as well as an alpha of 1.5. We are essentially taking the difference between the average image and the self portrait and emphasizing those differences in our self portrait. The result is below.

Bells and Whistles

For the bells and whistles, I created an animated face morph gif featuring 5 different faces. The characters are from the animated series Jojo's Bizarre Adventure, showcasing each protagonist of the first 5 parts!