Honestly, I'm not sure what to put for this write-up. There's just a lot of maths. What I did was I rewrote the system of equations such that I was minimizing the residual error. This becomes a least squares optimization problem that we can solve for a flattened H vector. This way, we are minimizing the L2-norm of Ah, so h of course has to be the eigenvector corresponding to the lowest eigenvalue of ATA.
Upon finding that H, I use inverse warping with the inverse of H to interpolate around what colour values I should reference.
Maybe it will make more sense to look at some examples! There are some pictures I took at IKEA one day when looking at some cute rooms.








Linear algebra is really cool. I honestly spent more time just writing out the set of equations and making the maths work more than anything else this assignment, which is great! One thing I want to note here is that when merging images, I used a one-shot method where I'd warp one image into another, bitwise and the images to find a region of overlap where we average the images and otherwise just use the regular images so there are no dark sections from halving their values.
For rectification, I used the points I took before from a bookshelf and thought about the viewpoint I'd want. Notice the slant in the image with the shelf. What if I could make the front part of the shelf square like instead of slanted? I hand defined my points to look more square like and made the homography accordingly.

I used the harris corners python script as given, then implemented ANMS. The function of ANMS is to space out the points we found previously. By eventually decrementing the radius we can fill up more and more points. Here is a side comparison of 1000 points, 750 points, and 500 points.

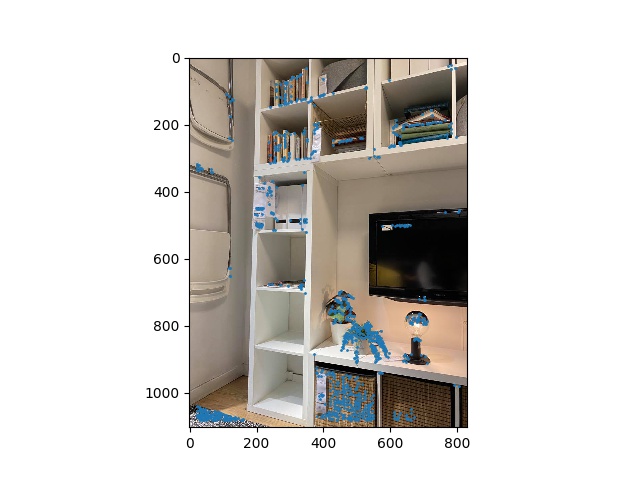
After this, I got a 40x40 patch for each point, used a gaussian blur (kernel 5x5), then downsampled to 8x8. I compare patches that have close enough SSD, then find the best match from that relatively good set. Now we have a bunch of corresponding sets of points! The problem is, these aren't perfectly matched. If we make a homography from this, it won't end well because of some mismatched points! We use RANSAC here to take out the bad points and eventually find a good match that can hit a bunch of inliers. Here are the side by side comparisons.





