For every line that is marked with a "# ?" symbol, try to determine what Python would print in the interactive interpreter. Then check to see if you got the answer right.
def square(x):
return x*x
def neg(f, x):
return -f(x)
# Q1
neg(square, 4)
_______________
# Q2
def first(x):
x += 8
def second(y):
print('second')
return x + y
print('first')
return second
f = first(15)
_______________
# Q3
f(16)
_______________
# Q4
def foo(x):
def bar(y):
return x + y
return bar
boom = foo(23)
boom(42)
_______________
# Q5
foo(6)(7)
_______________
# Q6
func = boom
func is boom
_______________
# Q7
func = foo(23)
func is boom
_______________
# Q8
def Troy():
abed = 0
while abed < 10:
britta = lambda: abed
abed += 1
annie = abed
annie += 1
abed = 20
return britta
jeff = Troy()
shirley = lambda : jeff
pierce = shirley()
pierce()
_______________
Define a function make_derivative that
returns a function: the derivative of a function f. Assuming that f is a
single-variable mathematical function, its derivative will also be a
single-variable function. When called with an int a, the derivative will compute the
slope of f at the point a.
The formula for finding the derivative of f at point a is
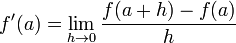
where h approaches 0. We will approximate the derivative
by setting h to a very small number: 0.00001.
The closer you make h to 0, the more accurate
the derivative approximation will be.
def make_derivative(f, h=1e-5):
"""Returns a function that is the derivative of f.
>>> square = lambda x: x*x
>>> derivative = make_derivative(square)
>>> result = derivative(3)
>>> round(result, 3)
6.0
"""
"*** YOUR CODE HERE ***"
Note: make_derivative itself is not the derivative; the function it returns is.
Now, we will visit the idea of helper functions. Sometimes, a function must perform a lot of computations -- so many computations, in fact, that it can get messy for the programmer to write. We can instead define a helper function within the parent function that will take care of some of the computations. The parent function then calls the helper function as needed.
Recall that a quadratic function is a function of the form:
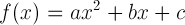
The quadratic equation is a classic algebraic formula used for finding the roots of quadratic functions. Part of the quadratic equation involves finding the discriminant (the part under the square root).
The quadratic equation is
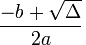
where the discriminant, represented by the delta, is
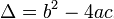
Define a function find_root that,
given the coefficients a, b, and
c of a quadratic function, will compute
a root of the function (normally, the quadratic equation has a
"+" or "-" sign -- we will focus on the "+" for now).
Your implementation should use a helper function called
discriminant, which also takes in the three
coefficients a, b, c, and computes their discriminant. Remember,
find_root is not returning
the function discriminant; rather,
find_root will call
discriminant to help with some calculations.
from math import sqrt
def find_root(a, b, c):
"""Returns one of two roots of a quadratic function.
Since there are two roots to quadratics, return the the larger
root. In other words, the + or - part of the quadratic equation
should just be replaced with a +
>>> find_root(1, 2, 1)
-1.0
>>> find_root(1, -7, 12)
4.0
"""
def discriminant(a, b, c):
"*** YOUR CODE HERE ***"
"*** YOUR CODE HERE ALSO ***"
Many procedures require a certain type of argument. For example, many arithmetic procedures only work if given numeric arguments. If given a non-number, an error results. For instance, pow('hello', 2) will result in the following error:
TypeError: unsupported operand type(s) for ** or pow(): 'str' and 'int'
Suppose we want to write safe versions of procedures, that can check if the argument is okay, and either call the underlying procedure or return False for a bad argument instead of giving an error. (We'll restrict our attention to procedures that take a single argument.)
>>> sqrt('hello')
Traceback (most recent call last):
File "", line 1, in
TypeError: a float is required
>>> type_check(sqrt, isnumber, 'hello')
False
>>> type_check(sqrt, isnumber, 4)
2.0
1.) Write type_check. Its arguments are a
function, a type-checking predicate that returns True
if and only if the datum is a legal argument to the function, and the
datum.
For testing, you'll want the isnumber
procedure: use the one here (you don't have to understand how it works):
def isnumber(thing):
try:
int(thing)
except:
return False
return True
2.) We really don’t want to have to use type_check explicitly every time. Instead, we’d like to be able to use a safe_sqrt procedure:
>>> safe_sqrt(’hello’) False >>> safe_sqrt(4) 2.0Don’t write safe_sqrt! Instead, write a procedure make_safe that you can use this way:
>>> safe_sqrt = make_safe(sqrt, isnumber)
It should take two arguments, a function (you can assume it takes exactly one argument) and a type-checking predicate, and return a new function that returns False if its argument doesn’t satisfy the predicate.Define a function cycle which takes in three functions as arguments: f1, f2, f3. cycle will then return another function. The returned fuction should take in an integer argument n and do the following:
Hint: most of the work goes inside the most nested function.
def cycle(f1, f2, f3):
""" Returns a function that is itself a higher order function
>>> add1 = lambda x: x+1
>>> times2 = lambda x: 2*x
>>> add3 = lambda x: x+3
>>> my_cycle = cycle(add1, times2, add3)
>>> identity = my_cycle(0)
>>> identity(5)
5
>>> add_one_then_double = my_cycle(2)
>>> add_one_then_double(1) # semanitcally the same as times2(add1(1))
4
>>> do_all_functions = my_cycle(3)
>>> do_all_functions(2) # semantically the same as add3(times2(add1(2)))
9
>>> do_more_than_a_cycle = my_cycle(4)
>>> do_more_than_a_cycle(2) # semantically the same as add1(add3(times2(add1(2))))
10
>>> do_two_cycles = my_cycle(6) # semantically the same as add3(times2(add1(add3(times2(add1(1))))))
>>> do_two_cycles(1)
19
"""
" *** YOUR CODE HERE *** "
Fin.