which just calls eval again!
When does it all end?

Eval calls apply,
which just calls eval again!
When does it all end?
In this project, you will develop an interpreter for a subset of the Scheme language. As you proceed, think about the issues that arise in the design of a programming language; many quirks of languages are the byproduct of implementation decisions in interpreters and compilers.
You will also implement some small programs in Scheme. Scheme is a simple but powerful functional language. You should find that much of what you have learned about Python transfers cleanly to Scheme as well as to other programming languages. To learn more about Scheme, you can read the original Structure and Interpretation of Computer Programs online for free. Examples from chapters 1 and 2 are included as test cases for this project. Language features from Chapters 3, 4, and 5 are not part of this project, but of course you are welcome to extend your interpreter to implement more of the language. Since we only include a subset of the language, your interpreter will not match exactly the behavior of other interpreters such as STk.
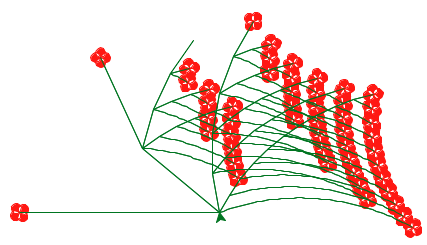
The project concludes with an open-ended graphics contest that challenges you to produce recursive images in only a few lines of Scheme. As an example of what you might create, the picture above abstractly depicts all the ways of making change for $0.50 using U.S. currency. All flowers appear at the end of a branch with length 50. Small angles in a branch indicate an additional coin, while large angles indicate a new currency denomination. In the contest, you too will have the chance to unleash your inner recursive artist.
This project includes several files, but all of your changes will be made
to the first four: scheme.py, scheme_reader.py,
questions.scm, and
tests.scm. You can download all of the
project code as a zip archive.
scheme.py |
The Scheme evaluator |
scheme_reader.py |
The Scheme syntactic analyzer |
questions.scm |
A collection of test cases written in Scheme |
tests.scm |
A collection of test cases written in Scheme |
scheme_tokens.py |
A tokenizer for scheme |
scheme_primitives.py |
Primitive Scheme procedures |
scheme_test.py |
A testing framework for Scheme |
scheme_grader.py |
A suite of tests for the project |
ucb.py |
Utility functions for 61A |
autograder.py |
Utility functions for grading |
This is a two-part, two-person project. All questions are labeled sequentially, but some are designated for certain people by a prefix of their letter (A or B). Both partners should understand the solutions to all questions.
In the first part, you will develop the interpreter in stages:
In the second part, you will implement Scheme procedures that are similar to some exercises that you previously completed in Python.
There are 27 possible correctness points and 3 composition points. The composition score in this project will evaluate the clarity of your code and your ability to write tests that verify the behavior of your interpreter.
Submit the project using submit proj4. The only files you are
required to submit are scheme.py, scheme_reader.py,
questions.scm,
and tests.scm.
Before you begin working on the project, review what you have learned in lecture about the Scheme language in Section 3.2 of Composing Programs.
Read-Eval-Print. The interpreter reads Scheme expressions, evaluates them, and prints the results.
scm> 2
2
scm> (((lambda (f) (lambda (x) (f f x)))
(lambda (f k) (if (zero? k) 1 (* k (f f (- k 1)))))) 5)
120
The starter code for your Scheme interpreter in scheme.py can
successfully evaluate the first expression above, since it consists of a
single number. The second (a computation of 5 factorial) will not work just
yet.
Load. Our load procedure differs from standard Scheme
in that we use a symbol for the file name. For example, to load
tests.scm, evaluate the following call
expression.
scm> (load 'tests)
Symbols. Unlike some implementations of Scheme, in this project numbers and boolean values cannot be used as symbols. Also, symbols are always lowercased.
scm> (define 2 3)
Traceback (most recent call last):
0 (#define 2 3)
Error: bad argument to define
scm> 'Hello
hello
Turtle Graphics. In addition to standard Scheme procedures, we
include procedure calls to the Python turtle package. You can
read the
turtle module documentation online.
Note: The turtle Python module may not
be installed by default on your personal computer. However, the
turtle module is installed on the instructional machines.
So, if you wish to create turtle graphics for this project (i.e. for
the contest), then you'll either need to setup turtle on
your personal computer or use university computers.
The tests.scm file contains a long
list of example Scheme expressions and their expected values.
(+ 1 2)
; expect 3
(/ 1 0)
; expect Error
You can compare the output of your interpreter to the expected output by
running scheme_test.py.
python3 scheme_test.py
For the example above, scheme_test.py will evaluate (+
1 2) using your code in scheme.py, then output a test
failure if 3 is not returned as the value. The second example
tests for an error (but not the specific error message).
Only a small subset of tests are designated to run by default because
tests.scm contains an (exit)
call near the beginning, which halts testing. As you complete more of the
project, you should move or remove this call. Note that your interpreter
doesn't know how to exit until Problems 3 and 4 are completed; all tests will
run until then.
Important: As you proceed in the project, add new tests to the top
of tests.scm to verify the behavior of
your implementation. Your composition score for this project will depend on
whether or not you have tested your implementation in ways that are different
from the autograder.
As always, you can run the doctests for the project.
python3 -m doctest scheme.py scheme_reader.py
You can also run the autograder tests.
python3 scheme_grader.py
python3 scheme_grader.py -q 1
Debugging. Try using the trace decorator from the
ucb module to follow the path of execution in your
interpreter.
Exceptions. As you develop your Scheme interpreter, you may find that Python raises
various uncaught exceptions when evaluating Scheme expressions. As a result,
your Scheme interpreter will halt. Some of these may be the results of bugs in
your program, and some may be useful indications of errors in user programs.
The former should be fixed (of course!) and the latter should be handled,
usually by raising a SchemeError. All SchemeError
exceptions are handled and printed as error messages by the
read_eval_print_loop function in scheme.py. Ideally,
there should never be unhandled Python exceptions for any input to your
interpreter.
To run your Scheme interpreter in an interactive mode, type:
python3 scheme.py
You can use your Scheme interpreter to evaluate the expressions in an input
file by passing the file name as a command-line argument to
scheme.py:
python3 scheme.py tests.scm
Currently, your Scheme interpreter can handle a few simple expressions, such
as:
scm> 1
1
scm> 42
42
scm> #t
True
To exit the Scheme interpreter, issue either Ctrl-c or
Ctrl-d or evaluate the exit procedure:
scm> (exit)
The function scheme_read in scheme_reader.py
parses a Buffer (buffer.py) instance that returns
valid Scheme tokens on invocations of current and
pop methods. This function returns the next full Scheme
expression in the src buffer, using this representation:
| Scheme Data Type | Our Internal Representation |
|---|---|
| Numbers | Python's built-in int and float data types.
|
| Symbols | Python's built-in string data type. |
Booleans (#t, #f) |
Python's built-in True, False
values. |
| Pairs | The Pair class, defined in
scheme_reader.py. |
| nil | The nil object, defined in
scheme_reader.py. |
Problem 1 (1 pt). Complete the scheme_read function in
scheme_reader.py by adding support for quotation. This function
dispatches on the type of the next token:
src is the string "nil",
return the nil object. (provided)
'bagel), then return a quote special form (such as
(quote bagel)).
"(", return the
result of read_tail. (provided)
Problem 2 (2 pt). Complete the read_tail function in
scheme_reader.py by adding support for dotted lists. A dotted
list in Scheme is not necessarily a well-formed list, but instead has an
arbitrary second attribute that may be any Scheme value.
The read_tail function expects to read the rest of a list or
dotted list, assuming the open parenthesis of that list has already been
popped by scheme_read.
Consider the case of calling scheme_read on input "(1 2
. 3)". The read_tail function will be called on the
suffix "1 2 . 3)", which is
1 and the value of
the tail "2 . 3)", which is
2 and the
Scheme value 3.read_tail would return Pair(1, Pair(2, 3)).
Hint: In order to verify that only one element follows a dot, after
encountering a '.', read one additional expression and then
check to see that a closing parenthesis follows.
To verify that your solutions to Problem 1 and 2 work correctly, run the
doctests for scheme_reader.py and test your parser interactively
by running,
# python3 scheme_reader.py
read> 42
42
read> '(1 2 3)
(quote (1 2 3))
read> nil
()
read> '()
(quote ())
read> (1 (2 3) (4 (5)))
(1 (2 3) (4 (5)))
read> (1 (9 8) . 7)
(1 (9 8) . 7)
read> (hi there . (cs . (student)))
(hi there cs student)
All further changes to the interpreter will be made in
scheme.py. For each question, add a few tests to the top of
tests.scm to verify the behavior of
your implementation.
In the implementation given to you, the scheme_eval function is
complete, but few of the functions or methods it uses are implemented. In
fact, the evaluator can only evaluate self-evaluating expressions: numbers,
booleans, and nil.
Problem 3 (2 pt). Implement apply_primitive, which is
called by scheme_apply. Primitive procedures are applied by
calling a corresponding Python function that implements the procedure.
Scheme primitive procedures are represented as instances of the
PrimitiveProcedure class, defined in
scheme_primitives.py. A PrimitiveProcedure has two
instance attributes:
fn is the use_env is a boolean flag that indicates whether or
not this primitive procedure will expect the current environment to be
passed in as the last argument. The environment is required, for instance,
to implement the primitive eval procedure.To see a list of all Scheme primitive procedures used in the project, look
in the scheme_primitives.py file. Any function decorated with
@primitive will be added to the globally-defined
_PRIMITIVES list.
The apply_primitive function takes a
PrimitiveProcedure instance, a Scheme list of argument values,
and the current environment. Your implementation should:
procedure.use_env is True, then
add the current environment env as the last argument.
procedure.fn on those arguments (hint: use *
notation).
TypeError exception
being thrown, then raise a SchemeError instead.The doctest for apply_primitive should now pass. However,
your Scheme interpreter will still not be able to apply primitive
procedures, because your Scheme interpreter still doesn't know
how to look up the values for the primitive procedure symbols (such as
+, *, and car).
Problem 4 (2 pt) Implement the lookup method of the
Frame class. It takes a symbol (Python string) and returns the
value bound to that name in the first frame of the environment in which it is
found. A Frame represents an environment via two instance
attributes:
bindings is a dictionary that maps Scheme symbol keys
(represented as Python strings) to Scheme values.
parent is the parent Frame
instance. The parent of the Global Frame is None.
lookup implementation should,
self.bindings if it exists.
lookup that symbol in the parent if it exists.
SchemeError. (provided)
After you complete this problem, you should be able to evaluate primitive procedure calls, giving you the functionality of the Calculator language and more.
scm> +
#[primitive]
scm> (+ 1 2)
3
scm> (* 3 4 (- 5 2) 1)
36
scm> (odd? 31)
True
Problem A5 (1 pt). There are two missing parts in the
do_define_form function, which handles the
(define ...) special forms. Implement just the first part,
which binds names to values but does not create new procedures.
do_define_form should return the name after performing the
binding.
scm> (define tau (* 2 3.1415926))
tau
You should now be able to give names to values and evaluate symbols to those values.
scm> (define x 15)
x
scm> (define y (* 2 x))
y
scm> y
30
scm> (+ y (* y 2) 1)
91
scm> (define x 20)
x
scm> x
20
Problem B6 (1 pt). Implement the do_quote_form
function, which evaluates the quote special form. Once you have
done so, you can evaluate quoted expressions.
scm> 'hello
hello
scm> '(1 . 2)
(1 . 2)
scm> '(1 (2 three . (4 . 5)))
(1 (2 three 4 . 5))
scm> (car '(a b))
a
scm> (eval (cons 'car '('(1 2))))
1
At this point in the project, your Scheme interpreter should be be able to support the following features:
quote special form,(+ (- 4 2) 5) User-defined procedures are represented as instances of the
LambdaProcedure class, defined in scheme.py. A
LambdaProcedure instance has three instance attributes:
formals is a Scheme list of the formal
parameters (symbols) that name the arguments of the procedure.
body is a single Scheme expression; the body of the
procedure.
env is the environment in which the procedure was
defined. Problem 7 (2 pt). First, implement the begin special
form, which includes a list of one or more sub-expressions that are each
evaluated in order. The value of the final sub-expression is the value of the
begin expression.
scm> (begin (+ 2 3) (+ 5 6))
11
scm> (begin (display 3) (newline) (+ 2 3))
3
5
scm> (begin (print 3) '(+ 2 3))
3
(+ 2 3)
Hint: When scheme_eval evaluates one of the
LOGICAL_FORMS in scheme.py, it calls
scheme_eval on the returned value. Take care that your
Scheme interpreter doesn't inadvertently call scheme_eval on the
same value twice, or else you might have the following incorrect behavior:
scm> (begin 30 'hello)
Error: unknown identifier: hello
Problem 8 (2 pt). Implement the do_lambda_form method,
which creates LambdaProcedure instances by evaluating
lambda expressions. While you cannot call a user-defined
procedure yet, you can verify that you have read the procedure correctly by
evaluating a lambda expression.
scm> (lambda (x y) (+ x y))
(lambda (x y) (+ x y))
In Scheme, it is legal to have function bodies with more than one expression.
In order to implement this feature, your do_lambda_form should
detect when the body of a lambda expression contains multiple expressions. If
so, then do_lambda_form should place those expressions inside of
a (begin ...) form, and use that begin expression as
the body:
scm> (lambda (y) (print y) (* y 2))
(lambda (y) (begin (print y) (* y 2)))
Problem A9 (1 pt). Currently, your Scheme interpreter is able to define user-defined procedures in the following manner:
scm> (define f (lambda (x) (* x 2)))
f
However, we'd like to be able to use the shorthand form of defining
procedures:
scm> (define (f x) (* x 2))
f
Modify the do_define_form function so that it correctly
handles the shorthand procedure definition form above. Make sure that it can
handle multi-expression bodies. Hint: construct a lambda
expression and evaluate it with do_lambda_form.
Once you have completed this problem, you should find that defined procedures evaluate to lambda procedures.
scm> (define (square x) (* x x))
square
scm> square
(lambda (x) (* x x))
Problem 10 (2 pt). Implement the make_call_frame method of
the Frame class, which:
Frame instance, the parent of which is self. (provided) SchemeError if make_call_frame receives
a different number of formal parameters and arguments.
Problem B11 (1 pt). Implement the check_formals
function to raise an error whenever the Scheme list of formal parameters
passed to it is invalid. Raise a SchemeError if the list of
formals is not a well-formed list of symbols or if any symbol is
repeated. (Hint: The symbol? procedure in
scheme_primitives.py returns whether a value is a Scheme symbol.)
Problem 12 (2 pt). Implement scheme_apply to correctly
apply user-defined LambdaProcedure instances. (The case of
MuProcedures is handled later in the project). It should:
Frame, with all formal parameters
bound to their argument values.
procedure in the environment
represented by this new frame.
procedure.
After you complete scheme_apply, user-defined functions (and
lambda functions) should work in your Scheme interpreter. Now is an excellent
time to revisit the tests in tests.scm
and ensure that you pass the ones that involve definition (Sections 1.1.2 and
1.1.4). You should also add additional tests of your own at the top of
tests.scm to verify that your interpreter is behaving as you
expect.
Logical special forms include if, and,
or, and cond. These expressions are special because
not all of their sub-expressions may be evaluated.
In Scheme, only #f (also known as false or
False) is a false value. All other values are true values. You
can test whether a value is a true value or a false value using the provided
Python functions scheme_true and scheme_false,
defined in scheme_primitives.py.
Problem A13 (1 pt). Implement do_if_form so that
if expressions are evaluated correctly. This function should
return either the second (consequent) or third (alternative) expression of
the if expression, depending on the value of the first
(predicate) expression.
scm> (if (= 4 2) true false)
False
scm> (if (= 4 4) (* 1 2) (+ 3 4))
2
It is legal to pass in just two expressions to the if special
form. In this case, you should return the second expression if the first
expression evaluates to a true value. Otherwise, return the special
okay value, which represents an undefined value.
scm> (if (= 4 2) true)
okay
Problem B14 (2 pt). Implement do_and_form and
do_or_form so that and and or
expressions are evaluated correctly.
The logical forms and and or are
short-circuiting. For and, your interpreter should
evaluate each sub-expression from left to right, and if any of these
evaluates to False, then False is returned. If
all but the last sub-expressions evaluate to true values, return the last
sub-expression from do_and_form.
For or, evaluate each sub-expression from left to right. If
any evaluates to a true value, then quote that value and return
it. These return values must be quoted because they are evaluated in
scheme_eval. If all but the last sub-expression evaluate to
false, return the last sub-expression from do_or_form without
quoting it.
scm> (and)
True
scm> (or)
False
scm> (and 4 5 6)
6 ; all operands are true values
scm> (or 5 2 1)
5 ; 5 is a true value
scm> (and #t #f 42 (/ 1 0))
False ; short-circuiting behavior of and
scm> (or 4 #t (/ 1 0))
4 ; short-circuiting behavior of or
Problem A15 (1 pt). Implement do_cond_form so that it
returns the first result sub-expression corresponding to a true predicate (or
else). Your implementation should match the following examples and the
additional tests in tests.scm.
scm> (cond ((= 4 3) 'nope)
((= 4 4) 'hi)
(else 'wait))
hi
scm> (cond ((= 4 3) 'wat)
((= 4 4))
(else 'hm))
True
scm> (cond ((= 4 4) 'here 42)
(else 'wat 0))
42
For the last example, where the body of a cond case has multiple
expressions, you might find it helpful to replace
cond-bodies with multiple expression bodies into a
single begin expression, i.e., the following two expressions are
equivalent.
(cond ((= 4 4) 'here 42))
(cond ((= 4 4) (begin 'here 42)))
If the body of a cond case is empty,
then do_cond_form should quote the value of the predicate and
return it, if the predicate evaluates to a true value.
scm> (cond (12))
12
scm> (cond ((= 4 3))
('hi))
hi
The value of a cond is undefined if there are no true
predicates and no else. In such a case, do_cond_form
should return okay.
Problem A16 (2 pt). The let special form introduces local
variables, giving them their initial values. For example,
scm> (define x 'hi)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
(y (* 5 10)))
(list x y))
(42 50)
scm> (list x y)
(hi bye)
Implement the do_let_form method to have this effect and test it,
by adding test cases to the top of tests.scm. Make sure your let
correctly handles multi-expression bodies:
scm> (let ((x 42)) x 1 2)
2
The let special form is equivalent to creating and then calling a lambda procedure. That is, the following two expressions are equivalent:
(let ((x 42) (y 16)) (+ x y))
((lambda (x y) (+ x y)) 42 16)
Thus, a let form creates a new Frame (containing the
let bindings) which extends the current environment and evaluates
the body of the let with respect to this new Frame.
In your project code, you don't have to actually create a
LambdaProcedure and call it. Instead, you can create a new
Frame, add the necessary bindings, and evaluate the expressions
of the let body in this new environment.
Problem B17 (2 pt). Implement do_mu_form to evaluate
the mu special form, a non-standard Scheme expression type. A
mu expression is similar to a lambda expression,
but evaluates to a MuProcedure instance that is dynamically
scoped. The MuProcedure class has been provided for you.
Additionally, complete scheme_apply to call
MuProcedure procedures using dynamic scoping. Calling a
LambdaProcedure uses lexical scoping: the parent of the new call
frame is the environment in which the procedure was defined. Calling a
MuProcedure created by a mu expression uses dynamic
scoping: the parent of the new call frame is the environment in which the
call expression was evaluated. As a result, a MuProcedure does
not need to store an environment as an instance attribute. It can refer to
names in the environment from which it was called.
scm> (define f (mu (x) (+ x y)))
f
scm> (define g (lambda (x y) (f (+ x x))))
g
scm> (g 3 7)
13
Your Scheme interpreter implementation is now complete. You should have
been adding tests to the top of tests.scm
as you did each problem. These tests will be evaluated as part of your
composition score for the project.
Not only is your Scheme interpreter itself a tree-recursive program, but it is
flexible enough to evaluate other recursive programs. Implement the following
procedures in Scheme in questions.scm.
Problem 18 (2 pt). Implement the merge procedure, which
takes in a comparator and two sorted list arguments and combines them into one
sorted list. A
scm> (merge < '(1 4 6) '(2 5 8))
(1 2 4 5 6 8)
scm> (merge > '(6 4 1) '(8 5 2))
(8 6 5 4 2 1)
Problem 19 (2 pt). Implement the list-partitions procedure,
which lists all of the ways to partition a positive integer total into at
most max-pieces pieces that are all less than or equal to a positive
integer max-value. Hint: Define a helper function to construct
partitions.
The number 5 has 4 partitions using pieces up to a
max-value of 3 and a max-pieces of
4:
3, 2 (two pieces)
3, 1, 1 (three pieces)
2, 2, 1 (three pieces)
2, 1, 1, 1 (four pieces)
Problem 20 (2 pt). You have been given the definition to an abstract
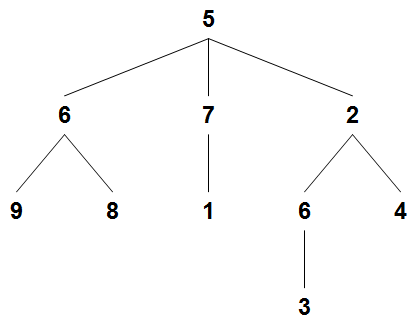
implementation of trees. Use it to implement tree-sums, which
is a function that returns a list of all possible sums of nodes, when
traversing from root to leaf. For example, the following tree when passed
through tree-sums will return
(20 19 13 16 11):
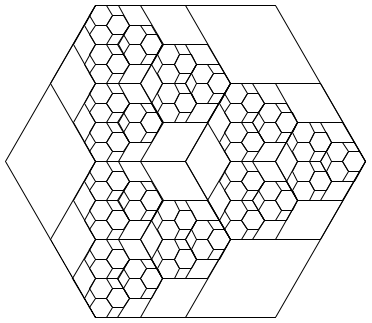
Problem 21 (0 pt). Implement the hax procedure that
draws the following recursive illustration when passed two arguments, a side
length d and recursive depth k. The example below
is drawn from (hax 200 4).
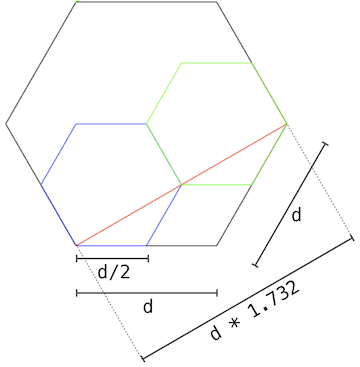
To see how this illustration is constructed, consider this annotated version that gives the relative lengths of lines of the component shapes in the figure.
Problem 22 (3 pt). Complete the function
scheme_optimized_eval
in scheme.py. This alternative to scheme_eval is
properly tail recursive. That is, the interpreter will allow an unbounded
number of active tail
calls in constant space.
Instead of recursively calling scheme_eval for tail calls and
logical special forms, and let, replace the current
expr and env with different expressions and
environments. For call expressions, this change only applies to calling
user-defined procedures.
Once you finish, uncomment the line
scheme_eval = scheme_optimized_eval in scheme.py.
Congratulations! You have finished the final project for 61A! Assuming your tests are good and you've passed them all, consider yourself a proper computer scientist!
Now, get some sleep. You've earned it!
We've added a number of primitive drawing procedures that are collectively
called "turtle graphics". The turtle represents the state of the drawing
module, which has a position, an orientation, a pen state (up or down), and a
pen color. The tscheme_x functions in
scheme_primitives.py are the implementations of these
procedures, and show their parameters with a brief description of each.
The Python documentation of
the turtle module contains more detail.
Contest. Create a visualization of an iterative or recursive process
of your choosing, using turtle graphics. Your implementation must be written
entirely in Scheme using the interpreter you have built. However, you may add
primitive procedures to interface with Python's turtle
or math modules. Other than that
all computation must be done in Scheme. If you do add new primitives,
then make sure to submit scheme_primitives.py in addition
to contest.scm.
Prizes will be awarded for the winning entry in each of the following categories, as well as 3 extra credit points.
Entries (code and results) will be posted online, and winners will be selected by popular vote as part of a future homework. The voting instructions will read:
Please vote for your favorite entry in this semester's 61A Recursion Exposition contest. The winner should exemplify the principles of elegance, beauty, and abstraction that are prized in the Berkeley computer science curriculum. As an academic community, we should strive to recognize and reward merit and achievement (translation: please don't just vote for your friends).
To improve your chance of success, you are welcome to include a title and descriptive haiku in the comments of your entry, which will be included in the voting.
Entries that do not construct an image iteratively or recursively may be disqualified. This includes just drawing a preexisting image, even if the drawing function is iterative or recursive.
Submission instructions will be posted on the course website.
We have implemented a significant subset of Scheme in this project, but our interpreter can be extended with more features by following the extension instructions.