Project 4: Scheme Interpreter (Challenge Version)

scheme_stubbed.zip

Eval calls apply,
which just calls eval again!
When does it all end?

Introduction

Important submission note: For full credit you must submit the entire project by Wednesday, 11/14. You will get an extra credit point for submitting the entire project by Tuesday, 11/13. Unlike the standard version of the project, there will be no checkpoints enforced. The two points corresponding to the checkpoint will be added to the points given for correctness.

We've written a language specification and built-in procedure reference for the CS 61A subset of Scheme that you'll be building in this project. You will not be responsible for implementing everything in these documents, but what you do implement should be consistent with the descriptions here.

This is an alternate "extreme" version of the standard Scheme project that gives you much less guidance than the normal version. It is only appropriate for students with substantial prior programming experience. Completing this version of the project is equivalent to completing the standard version of Project 4. Completing this version will not give you any more credit than is possible by completing the standard version - it's just here if you want a challenging experience.

Phase I of the project will be similar to the standard version, but the remaining parts will contain very little provided code. The final section, writing programs in Scheme, will be identical to the standard version.

You should not expect much assistance from staff if you choose to complete this version of the project. You can always switch to the standard version if you get stuck.

As a disclaimer, this version has not been tested to the same extent as the main project. It is functional to our understanding, but if you believe you've found an error in the specifications, tests, or provided files, please let us know on piazza and we will get it fixed as soon as possible.

Download starter files

You can download all of the project code as a zip archive. This project includes several files, but all of your changes will be made to only four: scheme.py, scheme_reader.py, questions.scm, and tests.scm. Here are all the files included in the archive:

scheme.py: implements the REPL and a evaluator for Scheme expressions
scheme_reader.py: implements the reader for Scheme input
scheme_tokens.py: implements the tokenizer for Scheme input
scheme_builtins.py: implements built-in Scheme procedures in Python
buffer.py: implements the Buffer class, used in scheme_reader.py
ucb.py: utility functions for use in 61A projects
questions.scm: contains skeleton code for Phase III
tests.scm: a collection of test cases written in Scheme
ok: the autograder
tests: a directory of tests used by ok

You may want to reference scheme_builtins in order to write tests and to use in your interpreter (for example, scheme_truep and scheme_falsep are helpful if you wish to test the truthiness of a value in Scheme).

Logistics

This is a 14-day project. You may work with one other partner. You should not share your code with students who are not your partner or copy from anyone else's solutions. In the end, you will submit one project for both partners.

Remember that you can earn an additional bonus point by submitting the project at least 24 hours before the deadline.

The project is worth 28 points. 26 points are assigned for correctness and 2 points for writing your own tests (Problem 0).

You will turn in the following files:

scheme_reader.py
scheme.py
questions.scm
tests.scm

You do not need to modify or turn in any other files to complete the project. To submit the project, run the following command:

python3 ok --submit

You will be able to view your submissions on the Ok dashboard.

For the functions that we ask you to complete, there may be some initial code that we provide. If you would rather not use that code, feel free to delete it and start from scratch. You may also add new function definitions as you see fit.

However, please do not modify any other functions. Doing so may result in your code failing our autograder tests. Also, please do not change any function signatures (names, argument order, or number of arguments).

Throughout this project, you should be testing the correctness of your code. It is good practice to test often, so that it is easy to isolate any problems. However, you should not be testing too often, to allow yourself time to think through problems.

We have provided an autograder called ok to help you with testing your code and tracking your progress. The first time you run the autograder, you will be asked to log in with your Ok account using your web browser. Please do so. Each time you run ok, it will back up your work and progress on our servers.

The primary purpose of ok is to test your implementations, but there are two things you should be aware of.

First, some of the test cases are locked. To unlock tests, run the following command from your terminal:

python3 ok -u

This command will start an interactive prompt that looks like:

=====================================================================
Assignment: Scheme Interpreter (Challenge Version)
Ok, version ...
=====================================================================

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Unlocking tests

At each "? ", type what you would expect the output to be.
Type exit() to quit

---------------------------------------------------------------------
Question 0 > Suite 1 > Case 1
(cases remaining: 1)

>>> Code here
?

At the ?, you can type what you expect the output to be. If you are correct, then this test case will be available the next time you run the autograder.

The idea is to understand conceptually what your program should do first, before you start writing any code.

Once you have unlocked some tests and written some code, you can check the correctness of your program using the tests that you have unlocked:

python3 ok

Most of the time, you will want to focus on a particular question. Use the -q option as directed in the problems below.

We recommend that you submit after you finish each problem. Only your last submission will be graded. It is also useful for us to have more backups of your code in case you run into a submission issue.

The tests folder is used to store autograder tests, so do not modify it. You may lose all your unlocking progress if you do. If you need to get a fresh copy, you can download the zip archive and copy it over, but you will need to start unlocking from scratch.

If you do not want us to record a backup of your work or information about your progress, use the --local option when invoking ok. With this option, no information will be sent to our course servers.

Interpreter details

Scheme features

Read-Eval-Print. The interpreter reads Scheme expressions, evaluates them, and displays the results.

scm> 2
2
scm> (+ 2 3)
5
scm> ((lambda (x) (* x x)) 5)
25

The starter code for your Scheme interpreter in scheme.py can successfully evaluate the first expression above, since it consists of a single number. The second (a call to a built-in procedure) and the third (a computation of 5 factorial) will not work just yet.

Load. You can load a file by passing in a symbol for the file name. For example, to load tests.scm, evaluate the following call expression.

scm> (load 'tests)

Symbols. Various dialects of Scheme are more or less permissive about identifiers (which serve as symbols and variable names).

Our rule is that:

An identifier is a sequence of letters (a-z and A-Z), digits, and characters in !$%&*/:<=>?@^_~-+. that do not form a valid integer or floating-point numeral.

Our version of Scheme is case-insensitive: two identifiers are considered identical if they match except possibly in the capitalization of letters. They are internally represented and printed in lower case:

scm> 'Hello
hello

Turtle Graphics. In addition to standard Scheme procedures, we include procedure calls to the Python turtle package. This will come in handy for the contest.

You can read the turtle module documentation online.

Note: The turtle Python module may not be installed by default on your personal computer. However, the turtle module is installed on the instructional machines. So, if you wish to create turtle graphics for this project (i.e. for the contest), then you'll either need to setup turtle on your personal computer or use university computers.

Implementation overview

Here is a brief overview of each of the Read-Eval-Print Loop components in our interpreter. Refer to this section as you work through the project as a reminder of how all the small pieces fit together!

Read: This step parses user input (a string of Scheme code) into our interpreter's internal Python representation of Scheme expressions (e.g. Pairs).
- Lexical analysis has already been implemented for you in the tokenize_lines function in scheme_tokens.py. This function returns a Buffer (from buffer.py) of tokens. You do not need to read or understand the code for this step.
- Syntactic analysis happens in scheme_reader.py, in the scheme_read and read_tail functions. Together, these mutually recursive functions parse Scheme tokens into our interpreter's internal Python representation of Scheme expressions. You will complete both functions.
Eval: This step evaluates Scheme expressions (represented in Python) to obtain values. Code for this step is in the main scheme.py file.
- Eval happens in the scheme_eval function. If the expression is a call expression, it gets evaluated according to the rules for evaluating call expressions (you will implement this). If the expression being evaluated is a special form, the corresponding do_?_form function is called. You will complete several of the do_?_form functions.
- Apply happens in the scheme_apply function. If the function is a built-in procedure, scheme_apply calls the apply method of that BuiltInProcedure instance. If the procedure is a user-defined procedure, scheme_apply creates a new call frame and calls eval_all on the body of the procedure, resulting in a mutually recursive eval-apply loop.
Print: This step prints the __str__ representation of the obtained value.
Loop: The logic for the loop is handled by the read_eval_print_loop function in scheme.py. You do not need to understand the entire implementation.

Exceptions. As you develop your Scheme interpreter, you may find that Python raises various uncaught exceptions when evaluating Scheme expressions. As a result, your Scheme interpreter will halt. Some of these may be the results of bugs in your program, but some might just be errors in user programs. The former should be fixed by debugging your interpreter and the latter should be handled, usually by raising a SchemeError. All SchemeError exceptions are handled and printed as error messages by the read_eval_print_loop function in scheme.py. Ideally, there should never be unhandled Python exceptions for any input to your interpreter.

Running the interpreter

To start an interactive Scheme interpreter session, type:

python3 scheme.py

You can use your Scheme interpreter to evaluate the expressions in an input file by passing the file name as a command-line argument to scheme.py:

python3 scheme.py tests.scm

Currently, your Scheme interpreter can handle a few simple expressions, such as:

scm> 1
1
scm> 42
42
scm> true
True

To exit the Scheme interpreter, press Ctrl-d or evaluate the exit procedure

scm> (exit)

Part 0: Testing Your Interpreter

The tests.scm file contains a long list of sample Scheme expressions and their expected values. Many of these examples are from Chapters 1 and 2 of Structure and Interpretation of Computer Programs, the textbook from which Composing Programs is adapted.

Problem 0 (2 pt)

Write tests as you go to verify that your interpreter works correctly. You will get full credit only if your custom tests are different than the provided OK tests, the provided tests.scm tests, and other Scheme assignments in this class.

The tests we provide for correctness are definitiely not comprehensive, even moreso for this version. It will be imperative to write your own tests as you progress through implementing the eval stage which check that your interpreter both correctly evaluates expressions and throws errors appropriately. If you ever get stuck or frustrated, writing a test or two can be a good way to make some progress and potentially gain insight into what needs to be done next. You may even wish to write tests before writing any code in accordance with the ideas of test-driven development.

Writing Tests. A test is written as a Scheme expression and the corresponding expected output:

<expr>
; expect <value>

Here are two examples:

(+ 1 2)
; expect 3
(/ 1 0)
; expect Error

The first example above tests if your interpreter correctly evaluates (+ 1 2). Specifically, the test will pass if your interpreter returns 3 as the value of that expression. The second example tests for a Scheme error (but not the specific error message). You should follow this format for your own tests.

Running Tests. You can compare the output of your interpreter to the expected output by running the following command:

python3 ok -q tests.scm

Only a small subset of tests are designated to run by default because tests.scm contains an (exit) call near the beginning, which halts testing. As you complete more of the project, you should move or remove this call. However, your interpreter doesn't know how to exit until your interpreter is able to call built-in procedures.

Part I: The Reader

All changes in this part should be made in scheme_reader.py.

The first part of this project deals with reading and parsing user input. Our reader will parse Scheme code into Python values with the following representations:

Input Example	Scheme Expression Type	Our Internal Representation
`scm> 1`	Numbers	Python's built-in `int` and `float` values
`scm> x`	Symbols	Python's built-in `string` values
`scm> #t`	Booleans (`#t`, `#f`)	Python's built-in `True`, `False` values
`scm> (+ 2 3)`	Combinations	Instances of the `Pair` class, defined in `scheme_reader.py`
`scm> nil`	`nil`	The `nil` object, defined in `scheme_reader.py`

For this project, we define combinations as both call expressions and special forms.

If you haven't already, make sure to read the Implementation overview section above to understand how the reader is broken up into parts.

In our implementation, we store tokens ready to be parsed in Buffer instances. For example, a buffer containing the input (+ (2 . 3)) would have the tokens '(', '+', '(', 2, '.', 3, ')', and ')'. See the doctests in buffer.py for more examples. You do not have to understand the code in this file.

You will write the parsing functionality, which consists of two mutually recursive functions scheme_read and read_tail. These functions each take in a single parameter, src, which is an instance of Buffer.

There are two methods defined in buffer.py that you'll use to interact with src:

src.remove_front(): mutates src by removing the first token in src and returns it. For the sake of simplicity, if we imagine src as a Python list such as [4, '.', 3, ')'], src.remove_front() will return 4, and src will be left with ['.', 3, ')'].
src.current(): returns the first token in src without removing it. For example, if src currently contains the tokens [4, '.', 3, ')'], then src.current() will return 4 but src will remain the same.

Problem 1 (3 pt)

Implement scheme_read and read_tail so that they can parse combinations, atomic expressions, and dotted pairs. Your final parser should also correctly handle quoted, quasiquoted, and unquoted expressions - you may implement that now or in the next question.

The expected behavior of the scheme_read and read_tail functions are as follows:

scheme_read removes enough tokens from src to form a single expression and returns that expression in the correct internal representation (see above table).
read_tail expects to read the rest of a list or pair, assuming the open parenthesis of that list or pair has already been removed by scheme_read. It will read expressions (and thus remove tokens) until the matching closing parenthesis ) is seen. This list of expressions is returned as a linked list of Pair instances.

In short, scheme_read returns the next single complete expression in the buffer and read_tail returns the rest of a list or pair in the buffer. Both functions mutate the buffer, removing the tokens that have already been processed.

After writing code, test your implementation:

python3 ok -q 01

Now that your parser is complete, you should also test it as follows:

Run the doctests for scheme_reader.py
```
python3 -m doctest scheme_reader.py -v
```

Test the read-eval-print loop by running python3 scheme_reader.py --repl. Every time you type in a value into the prompt, both the str and repr values of the parsed expression are printed. You can try the following inputs:

read> 42
str : 42
repr: 42
read> nil
str : ()
repr: nil
read> (1 (2 3) (4 (5)))
str : (1 (2 3) (4 (5)))
repr: Pair(1, Pair(Pair(2, Pair(3, nil)), Pair(Pair(4, Pair(Pair(5, nil), nil)), nil)))
read> (1 (9 8) . 7)
str : (1 (9 8) . 7)
repr: Pair(1, Pair(Pair(9, Pair(8, nil)), 7))
read> (hi there . (cs . (student)))
str : (hi there cs student)
repr: Pair('hi', Pair('there', Pair('cs', Pair('student', nil))))

Part II: The Evaluator

All changes in this part should be made in scheme.py and scheme_reader.py.

In scheme.py we've provided a function definition for scheme_eval - you should not change the signature of this function, as it is called in the read-eval-print-loop. However, the implementation of this function is up to you. It should be able to evaluate atomic expressions and combinations, including self-evaluating expressions, names, call expressions, and special forms.

Problem 2 (7 pt)

In this problem, you will implement the core functionality of the interpreter. You should fill in the scheme_eval function and add any necessary functions/classes so that your interpreter is able to do the following:

Evaluate self-evaluating atomic expressions including numbers, booleans, and nil
Evaluate symbols by looking up their value in the current environment
Apply built-in procedures (e.g. + and cons)
Evaluate call expressions
Add bindings to the current environment using the define special form.
Evaluate the quote special form
Evaluate the quasiquote and unquote special forms

At this point, you do not need to worry about creating user-defined procedures using the define special form (although you will in the next part). That is, your interpreter should be able to handle expressions such as (define x 1) but not (define (foo x) 1) after this question.

Remember to refer to the Scheme Specifications in order to determine the behavior of define (and other special forms).

The interpreter should raise a SchemeError if evaluating an unquote special form outside of a quasiquote special form. That is, The following expressions should cause a SchemeError:

,(+ 1 2)
`(1 ,(+ 2 ,(+ 3 4)))

However, the following expressions are allowed:

`(1 ,(+ 2 3))
`(1 ,(print `(2 ,(+ 3 4))))

We've provided a few classes that you will use in this part:

The Frame class is used to contain and organize the bindings in a specific frame. An instance of the Frame class is passed in to scheme_eval as env.
The BuiltinProcedure class inherits from the Procedure class (since your interpreter should handle both user-defined and built-in procedures). The constructor for a BuiltinProcedure creates two instance attributes
- fn is a Python function implementing the built-in scheme procedure
- use_env is a Boolean that indicates whether or not the built-in procedure expects the current environemnt to be passed in as the last argument. The environment is required, for instance, to implement the built-in eval procedure.

You may add any attributes or methods to these classes you see fit in order to implement the above functionality.

Here are some other tips for this question:

To see a list of all Scheme built-in procedures used in the project, look in the scheme_builtins.py file. Any function decorated with @builtin will be added to the globally-defined BUILTINS list. You can use any of these procedures in your tests.
You may want to take a look at some methods contained in the Pair class - for example, the map method of Pair can apply a one-argument function to every item in a Scheme list.
While built-in procedures follow the normal rules of evaluation (evaluate operator, evaluate operands, apply operator to operands), applying the operator does not create a new frame.
In order to implement the quote, unquote, and quasiquote special forms, you will have to both evaluate the expression correctly in the scheme_eval function and make sure your parser is able to correctly form these expressions. The output of the parser should substitute an equivalent expression using the quote, unquote, or quasiquote keywords if it sees one of the three following tokens: ' ` ,.
- For example, if the input string for the interpreter is `(a ,b), the output of the parser should be a Pair instance representing the expression (quasiquote (a (unquote b)))
Unquoting is fairly tricky to implement - specifically, figuring out whether or not an unquote is contained in a quasiquote. One approach is to, by default, have an attempt to evaluate an expression of the form (unquote ...) throw an error. However, if you come across an unquote while in the process of evaluating a quasiquote, you can handle it appropriately/
- Note that the actual behavior of unquoting is a lot more nuanced than this. For example, the expression `(a `,(1 ,(+ 2 3))) evaluates to (a (quasiquote (unquote (1 5)))). That is, the behavior of unquoting depends on its "depth".
  For this project, you may assume that if there are two nested quasiquotes without an intervening unquote, there will be no unquotes nested more deeply. That is, `(1 ,(cons a `(b ,c))) is a valid input, but `(1 `(cons b ,(c ,d))) is not.
  If you do want to attempt to implement the full functionality of quasiquoting, see the official Racket documentation which is what the staff interpreter implements.

Test your implementation before moving on:

python3 ok -q 02

After you complete this problem, your interpreter should be able to evalate the following expressions:

scm> +
#[+]
scm> odd?
#[odd?]
scm> display
#[display]

scm> (+ 1 2)
3
scm> (* 3 4 (- 5 2) 1)
36
scm> (odd? 31)
True

scm> (define x 15)
x
scm> x
15
scm> (eval 'x)
15
scm> (define y (* 2 x))
y
scm> y
30
scm> (+ y (* y 2) 1)
91
scm> (define x 20)
x
scm> x
20

scm> (quote a)
a
scm> (quote (1 . 2))
(1 . 2)
scm> (quote (1 (2 three . (4 . 5))))
(1 (2 three 4 . 5))
scm> 'hello
hello
scm> '(1 (2 three . (4 . 5)))
(1 (2 three 4 . 5))
scm> (eval (cons 'car '('(1 2))))
1
scm> `(1 ,(+ 1 1) 3)
(1 2 3)

Problem 3 (6 pt)

In this problem, you will implement user-defined expressions and some related features. After this, your interpreter should be able to accomplish the following:

Evaluate begin and lambda special forms
Create user-defined functions when evaluating the define special form
Apply lambda functions and user-defined procedures to arguments in a call expression

Although you added some functionality for call expressions in the previous part, user-defined procedures require some special handling. In particular, built-in procedures do not require creating new frames when you call them. However, user-defined procedures will require creating a new Frame (which we will use in accordance with the rules for calling functions we've learned in the class so far).

Here are some additional hints and clarifications:

A begin special form should evaluate to an undefined value if there are no sub-expressions to evaluate. The way we will represent this in the interpreter is by returning the Python value None.
User-defined procedures in Scheme are the same as lambda procedures. For example, the expression (define (foo x) x) binds the value (lambda (x) x) to the name foo in the current environment.
The body of a procedure can contain multiple expressions, which will be represented as a list of expressions. Only the value that the final expression evaluates to will be returned by the function call.

Here are some examples of expressions your interpreter should now be able to evaluate:

scm> (begin (print 3) '(+ 2 3))
3
(+ 2 3)
scm> (define x (begin (display 3) (newline) (+ 2 3)))
3
x

scm> (lambda (x y) (+ x y))
(lambda (x y) (+ x y))
scm> ((lambda (x y) (+ x y)) 1 2)
3

scm> (define (square x) (* x x))
square
scm> square
(lambda (x) (* x x))
scm> (square 4)
16

scm> (define (print-twice x) (print x) (print x))
print-twice
scm> (print-twice 1)
1
1

Test your implementation before moving on:

python3 ok -q 03

Problem 4 (5 pt)

In this part, you will be implementing the following special forms:

if
and/or
if/cond
let
mu

Make sure to read the Scheme Specifications for informaion on these special forms. Here are some clarifications on their behavior which are not mentioned in the specifications.

and and or should exhibit short-circuiting behavior as in Python and evaluate left to right.
mu procedures follow the same evaluation rules as lambda procedures (evaluate the operator, evaluate the operand, apply the operator to the operands). However, mu procedures are dynamically scoped - meaning the Frame created by calling a mu procedure should have its parent as the Frame it is called in, not the Frame it was defined in.

Test your implementation before moving on:

python3 ok -q 04

Your interpreter should now be able to evaluate the following expressions (and more)!

scm> (and)
#t
scm> (and 4 5 (+ 3 3))
6
scm> (and #t #f 42 (/ 1 0))  ; short-circuiting behavior of and
#f
scm> (or)
#f
scm> (or #f (- 1 1) 1)  ; 0 is a true value in Scheme
0
scm> (or 4 #t (/ 1 0))  ; short-circuiting behavior of or
4

scm> (cond ((= 4 3) 'nope)
           ((= 4 4) 'hi)
           (else 'wait))
hi
scm> (cond ((= 4 3) 'wat)
           ((= 4 4))
           (else 'hm))
True
scm> (cond ((= 4 4) 'here (+ 40 2))
           (else 'wat 0))
42

scm> (cond (False 1) (False 2))
scm>

scm> (define x 5)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
           (y (* x 10)))  ; x refers to the global value of x, not 42
       (list x y))
(42 50)
scm> (list x y)
(5 bye)

scm> (define f (mu () (* a b)))
f
scm> (define g (lambda () (define a 4) (define b 5) (f)))
g
scm> (g)
20

Part III: Write Some Scheme

Not only is your Scheme interpreter itself a tree-recursive program, but it is flexible enough to evaluate other recursive programs. Implement the following procedures in Scheme in the questions.scm file.

In addition, for this part of the project, you may find the built-in procedure reference very helpful if you ever have a question about the behavior of a built-in Scheme procedure, like the difference between pair? and list?.

The autograder tests for the interpreter are not comprehensive, so you may have uncaught bugs in your implementation. Therefore, you may find it useful to test your code for these questions in the staff interpreter or the web editor and then try it in your own interpreter once you are confident your Scheme code is working.

Problem 5 (1 pt)

Implement the enumerate procedure, which takes in a list of values and returns a list of two-element lists, where the first element is the index of the value, and the second element is the value itself.

scm> (enumerate '(3 4 5 6))
((0 3) (1 4) (2 5) (3 6))
scm> (enumerate '())
()

Test your implementation before moving on:

python3 ok -q 05

Problem 6 (2 pt)

Implement the list-change procedure, which lists all of the ways to make change for a positive integer total amount of money, using a list of currency denominations, which is sorted in descending order. The resulting list of ways of making change should also be returned in descending order.

To make change for 10 with the denominations (25, 10, 5, 1), we get the possibliites:

10
5, 5
5, 1, 1, 1, 1, 1
1, 1, 1, 1, 1, 1, 1, 1, 1, 1

To make change for 5 with the denominations (4, 3, 2, 1), we get the possibilities:

4, 1
3, 2
3, 1, 1
2, 2, 1
2, 1, 1, 1
1, 1, 1, 1, 1

You may find that implementing a helper function, cons-all, will be useful for this problem. To implement cons-all, use the built-in map procedure. cons-all takes in an element first and a list of lists rests, and adds first to the beginning of each list in rests:

scm> (cons-all 1 '((2 3) (2 4) (3 5)))
((1 2 3) (1 2 4) (1 3 5))

You may also find the built-in append procedure useful.

Test your implementation before moving on:

python3 ok -q 06

Problem 7 (2 pt)

In Scheme, source code is data. Every non-atomic expression is written as a Scheme list, so we can write procedures that manipulate other programs just as we write procedures that manipulate lists.

Rewriting programs can be useful: we can write an interpreter that only handles a small core of the language, and then write a procedure that converts other special forms into the core language before a program is passed to the interpreter.

For example, the let special form is equivalent to a call expression that begins with a lambda expression. Both create a new frame extending the current environment and evaluate a body within that new environment.

(let ((a 1) (b 2)) (+ a b))
;; Is equivalent to:
((lambda (a b) (+ a b)) 1 2)

These expressions can be represented by the following diagrams:

Let	Lambda

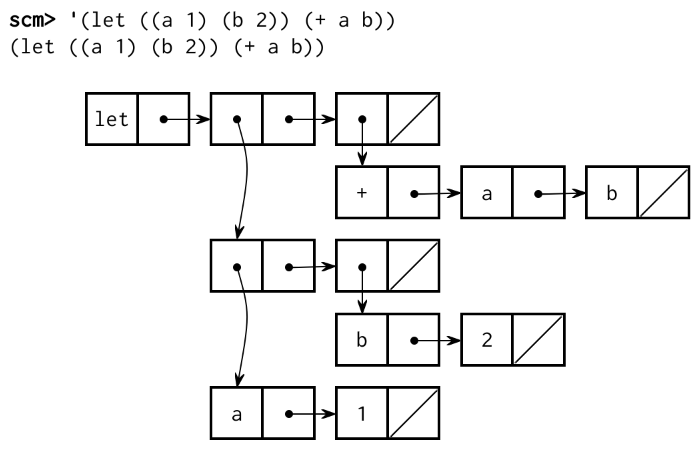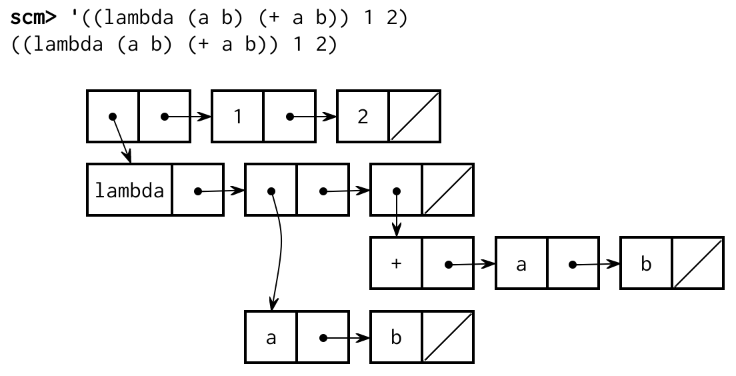Use this rule to implement a procedure called let-to-lambda that rewrites all let special forms into lambda expressions. If we quote a let expression and pass it into this procedure, an equivalent lambda expression should be returned: pass it into this procedure:

scm> (let-to-lambda '(let ((a 1) (b 2)) (+ a b)))
((lambda (a b) (+ a b)) 1 2)
scm> (let-to-lambda '(let ((a 1)) (let ((b a)) b)))
((lambda (a) ((lambda (b) b) a)) 1)

In order to handle all programs, let-to-lambda must be aware of Scheme syntax. Since Scheme expressions are recursively nested, let-to-lambda must also be recursive. In fact, the structure of let-to-lambda is somewhat similar to that of scheme_eval--but in Scheme! As a reminder, atoms include numbers, booleans, nil, and symbols. You do not need to consider code that contains quasiquotation for this problem.

(define (let-to-lambda expr)
  (cond ((atom?   expr) <rewrite atoms>)
        ((quoted? expr) <rewrite quoted expressions>)
        ((lambda? expr) <rewrite lambda expressions>)
        ((define? expr) <rewrite define expressions>)
        ((let?    expr) <rewrite let expressions>)
        (else           <rewrite other expressions>)))

Hint: You may want to implement zip at the top of questions.scm and also use the built-in map procedure.
scm> (zip '((1 2) (3 4) (5 6)))
((1 3 5) (2 4 6))
scm> (zip '((1 2)))
((1) (2))
scm> (zip '())
(() ())

Test your implementation by running

python3 ok -q 07

Note: We used let while defining let-to-lambda. What if we want to run let-to-lambda on an interpreter that does not recognize let? We can pass let-to-lambda to itself to rewrite itself into an equivalent program without let:
;; The let-to-lambda procedure
(define (let-to-lambda expr)
  ...)

;; A list representing the let-to-lambda procedure
(define let-to-lambda-code
  '(define (let-to-lambda expr)
     ...))

;; An let-to-lambda procedure that does not use 'let'!
(define let-to-lambda-without-let
  (let-to-lambda let-to-lambda-code))

Part IV: Extra Credit

Note: During regular Office Hours and Project Parties, the staff will prioritize helping students with required questions. We will not be offering help with either extra credit problems unless the queue is empty.

Problem 8 (2 pt)

Modify your interpreter to allow for evaluation that is properly tail recursive. That is, the interpreter will allow an unbounded number of active tail calls in constant space.

One way to implement tail recursive behavior is to delay the evaluation of expressions in tail contexts and then evaluate it at a later time. You can do this by wrapping an expression in a thunk. A thunk should contain all the information needed to evaluate that expression even outside the frame of scheme_eval.

You will then have to modify your scheme_eval function to:

Determine whether or not an expression is in a tail context and create thunks as appropriate
Handle evaluation of thunks if one is passed in to scheme_eval

You should not change the order or types of arguments to scheme_eval although you may wish to change the type of the third argument.

You will likely have to modify other parts of the program besides scheme_eval in order to determine which expressions are in tail contexts.

After you have implemented tail recursion, you will need to modify the implementation of complete_apply. This function is needed to implement the built-in apply procedure, as well as a few other built-in procedures. You may additionally find it useful for your own code.

Currently, complete_apply just returns the result of calling scheme_apply. However, complete_apply differs from scheme_apply in that it should never return a thunk. Therefore, if scheme_apply returns a thunk, you should extract and evaluate the expression contained inside the thunk instead, ensuring that you do not return a thunk.

Test your implementation using

python3 ok -q 08

Problem 9 (1 pt)

Macros allow the language itself to be extended by the user. Simple macros can be provided with the define-macro special form. This must be used like a procedure definition, and it creates a procedure just like define. However, this procedure has a special evaluation rule: it is applied to its arguments without first evaluating them. Then the result of this application is evaluated.

This final evaluation step takes place in the caller's frame, as if the return value from the macro was literally pasted into the code in place of the macro.

Here is a simple example:

scm> (define (map f lst) (if (null? lst) nil (cons (f (car lst)) (map f (cdr lst)))))
scm> (define-macro (for formal iterable body)
....     (list 'map (list 'lambda (list formal) body) iterable))
scm> (for i '(1 2 3)
....     (print (* i i)))
1
4
9
(None None None)

The code above defines a macro for that acts as a map except that it doesn't need a lambda around the body.

In order to implement define-macro, implement complete the implementation for do_define_macro, which should create a MacroProcedure and bind it to the given name as in do_define_form. Then, update scheme_eval so that calls to macro procedures are evaluated correctly.

Test your implementation before moving on:

python3 ok -q 09

Conclusion

Congratulations! You have just implemented an interpreter for an entire language! If you enjoyed this project and want to extend it further, you may be interested in looking at more advanced features, like let* and letrec, unquote splicing, error tracing, and continuations.

Unlike the "standard" version of your project, your interpreter does not have support for streams. In order to implement streams, you'll need to implement the delay and cons-stream special forms, as well as the built-in procedures promise?, force, and cdr-stream (which you could add to scheme_builtins.py).

If you wanted to implement streams for fun, you would want to add a Promise object to your interpreter, created by the delay special form.