Due by 11:59pm on Monday, October 14

Instructions

Download hw04.zip. Inside the archive, you will find a file called hw04.py, along with a copy of the ok autograder.

Submission: When you are done, submit with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be scored. Check that you have successfully submitted your code on okpy.org. See Lab 0 for more instructions on submitting assignments.

Using Ok: If you have any questions about using Ok, please refer to this guide.

Readings: You might find the following references useful:

• Section 2.2
• Section 2.3
• Section 2.4

Grading: Homework is graded based on effort, not correctness. However, there is no partial credit; you must show substantial effort on every problem to receive any points. This homework is out of 4 points.

Required questions

Abstraction

Q1: Taxicab Distance

An intersection in midtown Manhattan can be identified by an avenue and a street, which are both indexed by positive integers. The Manhattan distance or taxicab distance between two intersections is the number of blocks that must be traversed to reach one from the other, ignoring one-way street restrictions and construction. For example, Times Square is on 46th Street and 7th Avenue. Ess-a-Bagel is on 51st Street and 3rd Avenue. The taxicab distance between them is 9 blocks (5 blocks from 46th to 51st street and 4 blocks from 7th avenue to 3rd avenue). Taxicabs cannot cut diagonally through buildings to reach their destination!

Implement taxicab, which computes the taxicab distance between two intersections using the following data abstraction. Hint: You don't need to know what a Cantor pairing function is; just use the abstraction.

def intersection(st, ave):
    """Represent an intersection using the Cantor pairing function."""
    return (st+ave)*(st+ave+1)//2 + ave

def street(inter):
    return w(inter) - avenue(inter)

def avenue(inter):
    return inter - (w(inter) ** 2 + w(inter)) // 2

w = lambda z: int(((8*z+1)**0.5-1)/2)

def taxicab(a, b):
    """Return the taxicab distance between two intersections.

    >>> times_square = intersection(46, 7)
    >>> ess_a_bagel = intersection(51, 3)
    >>> taxicab(times_square, ess_a_bagel)
    9
    >>> taxicab(ess_a_bagel, times_square)
    9
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q taxicab

Mobiles

Acknowledgements. This mobile example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.2.2.

Hint: for more information on this problem (with more pictures!) please refer to this document

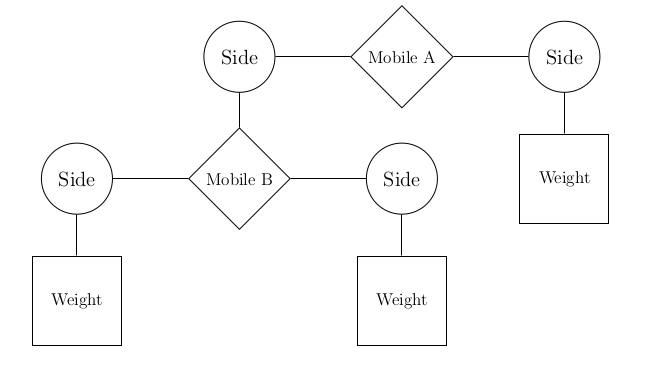
A mobile is a type of hanging sculpture. A binary mobile consists of two sides. Each side is a rod of a certain length, from which hangs either a weight or another mobile.

We will represent a binary mobile using the data abstractions below.

• A mobile has a left side and a right side.
• A side has a positive length and something hanging at the end, either a mobile or weight.
• A weight has a positive size.

Q2: Weights

Implement the weight data abstraction by completing the weight constructor and the size selector so that a weight is represented using a two-element list where the first element is the string 'weight'. The total_weight example is provided to demonstrate use of the mobile, side, and weight abstractions.

def mobile(left, right):
    """Construct a mobile from a left side and a right side."""
    assert is_side(left), "left must be a side"
    assert is_side(right), "right must be a side"
    return ['mobile', left, right]

def is_mobile(m):
    """Return whether m is a mobile."""
    return type(m) == list and len(m) == 3 and m[0] == 'mobile'

def left(m):
    """Select the left side of a mobile."""
    assert is_mobile(m), "must call left on a mobile"
    return m[1]

def right(m):
    """Select the right side of a mobile."""
    assert is_mobile(m), "must call right on a mobile"
    return m[2]

def side(length, mobile_or_weight):
    """Construct a side: a length of rod with a mobile or weight at the end."""
    assert is_mobile(mobile_or_weight) or is_weight(mobile_or_weight)
    return ['side', length, mobile_or_weight]

def is_side(s):
    """Return whether s is a side."""
    return type(s) == list and len(s) == 3 and s[0] == 'side'

def length(s):
    """Select the length of a side."""
    assert is_side(s), "must call length on a side"
    return s[1]

def end(s):
    """Select the mobile or weight hanging at the end of a side."""
    assert is_side(s), "must call end on a side"
    return s[2]

def weight(size):
    """Construct a weight of some size."""
    assert size > 0
    "*** YOUR CODE HERE ***"

def size(w):
    """Select the size of a weight."""
    assert is_weight(w), 'must call size on a weight'
    "*** YOUR CODE HERE ***"

def is_weight(w):
    """Whether w is a weight."""
    return type(w) == list and len(w) == 2 and w[0] == 'weight'

def total_weight(m):
    """Return the total weight of m, a weight or mobile.

    >>> t, u, v = examples()
    >>> total_weight(t)
    3
    >>> total_weight(u)
    6
    >>> total_weight(v)
    9
    """
    if is_weight(m):
        return size(m)
    else:
        assert is_mobile(m), "must get total weight of a mobile or a weight"
        return total_weight(end(left(m))) + total_weight(end(right(m)))

Use Ok to test your code:

python3 ok -q total_weight

Q3: Balanced

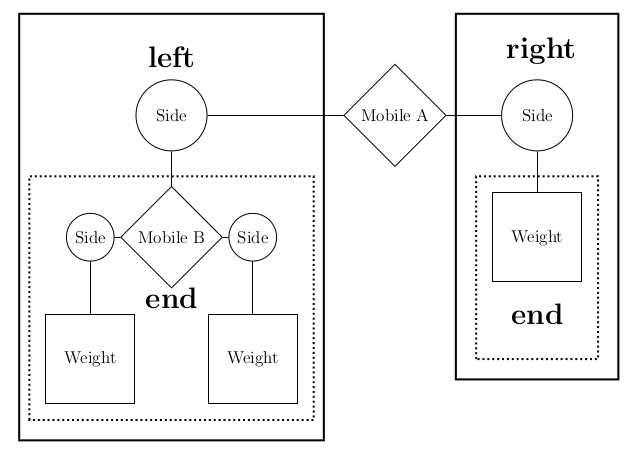
Hint: for more information on this problem (with more pictures!) please refer to this document

Implement the balanced function, which returns whether m is a balanced mobile. A mobile is balanced if two conditions are met:

1. The torque applied by its left side is equal to that applied by its right side. Torque of the left side is the length of the left rod multiplied by the total weight hanging from that rod. Likewise for the right.
2. Each of the mobiles hanging at the end of its sides is balanced.

Hint: You may find it helpful to assume that weights themselves are balanced.

def balanced(m):
    """Return whether m is balanced.

    >>> t, u, v = examples()
    >>> balanced(t)
    True
    >>> balanced(v)
    True
    >>> w = mobile(side(3, t), side(2, u))
    >>> balanced(w)
    False
    >>> balanced(mobile(side(1, v), side(1, w)))
    False
    >>> balanced(mobile(side(1, w), side(1, v)))
    False
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q balanced

Q4: Totals

Implement totals_tree, which takes a mobile (or weight) and returns a tree whose root is its total weight and whose branches are trees for the ends of the sides.

def totals_tree(m):
    """Return a tree representing the mobile with its total weight at the root.

    >>> t, u, v = examples()
    >>> print_tree(totals_tree(t))
    3
      2
      1
    >>> print_tree(totals_tree(u))
    6
      1
      5
        3
        2
    >>> print_tree(totals_tree(v))
    9
      3
        2
        1
      6
        1
        5
          3
          2
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q totals_tree

Trees

Q5: Replace Leaf

Define replace_leaf, which takes a tree t, a value old, and a value new. replace_leaf returns a new tree that's the same as t except that every leaf value equal to old has been replaced with new.

def replace_leaf(t, old, new):
    """Returns a new tree where every leaf value equal to old has
    been replaced with new.

    >>> yggdrasil = tree('odin',
    ...                  [tree('balder',
    ...                        [tree('thor'),
    ...                         tree('freya')]),
    ...                   tree('frigg',
    ...                        [tree('thor')]),
    ...                   tree('thor',
    ...                        [tree('sif'),
    ...                         tree('thor')]),
    ...                   tree('thor')])
    >>> laerad = copy_tree(yggdrasil) # copy yggdrasil for testing purposes
    >>> print_tree(replace_leaf(yggdrasil, 'thor', 'freya'))
    odin
      balder
        freya
        freya
      frigg
        freya
      thor
        sif
        freya
      freya
    >>> laerad == yggdrasil # Make sure original tree is unmodified
    True
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q replace_leaf

Nonlocal

Q6: Next Fibonacci

Write a function make_fib that returns a function that returns the next Fibonacci number each time it is called. (The Fibonacci sequence begins with 0 and then 1, after which each element is the sum of the preceding two.) Use a nonlocal statement!

def make_fib():
    """Returns a function that returns the next Fibonacci number
    every time it is called.

    >>> fib = make_fib()
    >>> fib()
    0
    >>> fib()
    1
    >>> fib()
    1
    >>> fib()
    2
    >>> fib()
    3
    >>> fib2 = make_fib()
    >>> fib() + sum([fib2() for _ in range(5)])
    12
    >>> from construct_check import check
    >>> # Do not use lists in your implementation
    >>> check(this_file, 'make_fib', ['List'])
    True
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q make_fib

Q7: Password Protected Account

In lecture, we saw how to use functions to create mutable objects. Here, for example, is the function make_withdraw which produces a function that can withdraw money from an account:

def make_withdraw(balance):
    """Return a withdraw function with BALANCE as its starting balance.
    >>> withdraw = make_withdraw(1000)
    >>> withdraw(100)
    900
    >>> withdraw(100)
    800
    >>> withdraw(900)
    'Insufficient funds'
    """
    def withdraw(amount):
        nonlocal balance
        if amount > balance:
           return 'Insufficient funds'
        balance = balance - amount
        return balance
    return withdraw

Write a version of the make_withdraw function that returns password-protected withdraw functions. That is, make_withdraw should take a password argument (a string) in addition to an initial balance. The returned function should take two arguments: an amount to withdraw and a password.

A password-protected withdraw function should only process withdrawals that include a password that matches the original. Upon receiving an incorrect password, the function should:

1. Store that incorrect password in a list, and
2. Return the string 'Incorrect password'.

If a withdraw function has been called three times with incorrect passwords <p1>, <p2>, and <p3>, then it is locked. All subsequent calls to the function should return:

"Your account is locked. Attempts: [<p1>, <p2>, <p3>]"

The incorrect passwords may be the same or different:

def make_withdraw(balance, password):
    """Return a password-protected withdraw function.

    >>> w = make_withdraw(100, 'hax0r')
    >>> w(25, 'hax0r')
    75
    >>> error = w(90, 'hax0r')
    >>> error
    'Insufficient funds'
    >>> error = w(25, 'hwat')
    >>> error
    'Incorrect password'
    >>> new_bal = w(25, 'hax0r')
    >>> new_bal
    50
    >>> w(75, 'a')
    'Incorrect password'
    >>> w(10, 'hax0r')
    40
    >>> w(20, 'n00b')
    'Incorrect password'
    >>> w(10, 'hax0r')
    "Your account is locked. Attempts: ['hwat', 'a', 'n00b']"
    >>> w(10, 'l33t')
    "Your account is locked. Attempts: ['hwat', 'a', 'n00b']"
    >>> type(w(10, 'l33t')) == str
    True
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q make_withdraw

Q8: Joint Account

Suppose that our banking system requires the ability to make joint accounts. Define a function make_joint that takes three arguments.

1. A password-protected withdraw function,
2. The password with which that withdraw function was defined, and
3. A new password that can also access the original account.

The make_joint function returns a withdraw function that provides additional access to the original account using either the new or old password. Both functions draw from the same balance. Incorrect passwords provided to either function will be stored and cause the functions to be locked after three wrong attempts.

Hint: The solution is short (less than 10 lines) and contains no string literals! The key is to call withdraw with the right password and amount, then interpret the result. You may assume that all failed attempts to withdraw will return some string (for incorrect passwords, locked accounts, or insufficient funds), while successful withdrawals will return a number.

Use type(value) == str to test if some value is a string:

def make_joint(withdraw, old_password, new_password):
    """Return a password-protected withdraw function that has joint access to
    the balance of withdraw.

    >>> w = make_withdraw(100, 'hax0r')
    >>> w(25, 'hax0r')
    75
    >>> make_joint(w, 'my', 'secret')
    'Incorrect password'
    >>> j = make_joint(w, 'hax0r', 'secret')
    >>> w(25, 'secret')
    'Incorrect password'
    >>> j(25, 'secret')
    50
    >>> j(25, 'hax0r')
    25
    >>> j(100, 'secret')
    'Insufficient funds'

    >>> j2 = make_joint(j, 'secret', 'code')
    >>> j2(5, 'code')
    20
    >>> j2(5, 'secret')
    15
    >>> j2(5, 'hax0r')
    10

    >>> j2(25, 'password')
    'Incorrect password'
    >>> j2(5, 'secret')
    "Your account is locked. Attempts: ['my', 'secret', 'password']"
    >>> j(5, 'secret')
    "Your account is locked. Attempts: ['my', 'secret', 'password']"
    >>> w(5, 'hax0r')
    "Your account is locked. Attempts: ['my', 'secret', 'password']"
    >>> make_joint(w, 'hax0r', 'hello')
    "Your account is locked. Attempts: ['my', 'secret', 'password']"
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q make_joint

Extra Questions

Q9: Interval Abstraction

Alyssa's program is incomplete because she has not specified the implementation of the interval abstraction. She has implemented the constructor for you; fill in the implementation of the selectors.

def interval(a, b):
    """Construct an interval from a to b."""
    return [a, b]

def lower_bound(x):
    """Return the lower bound of interval x."""
    "*** YOUR CODE HERE ***"

def upper_bound(x):
    """Return the upper bound of interval x."""
    "*** YOUR CODE HERE ***"

Use Ok to unlock and test your code:

python3 ok -q interval -u
python3 ok -q interval

Louis Reasoner has also provided an implementation of interval multiplication. Beware: there are some data abstraction violations, so help him fix his code before someone sets it on fire.

def mul_interval(x, y):
    """Return the interval that contains the product of any value in x and any
    value in y."""
    p1 = x[0] * y[0]
    p2 = x[0] * y[1]
    p3 = x[1] * y[0]
    p4 = x[1] * y[1]
    return [min(p1, p2, p3, p4), max(p1, p2, p3, p4)]

Use Ok to unlock and test your code:

python3 ok -q mul_interval -u
python3 ok -q mul_interval

Q10: Sub Interval

Using reasoning analogous to Alyssa's, define a subtraction function for intervals. Try to reuse functions that have already been implemented if you find yourself repeating code.

def sub_interval(x, y):
    """Return the interval that contains the difference between any value in x
    and any value in y."""
    "*** YOUR CODE HERE ***"

Use Ok to unlock and test your code:

python3 ok -q sub_interval -u
python3 ok -q sub_interval

Q11: Div Interval

Alyssa implements division below by multiplying by the reciprocal of y. Ben Bitdiddle, an expert systems programmer, looks over Alyssa's shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Add an assert statement to Alyssa's code to ensure that no such interval is used as a divisor:

def div_interval(x, y):
    """Return the interval that contains the quotient of any value in x divided by
    any value in y. Division is implemented as the multiplication of x by the
    reciprocal of y."""
    "*** YOUR CODE HERE ***"
    reciprocal_y = interval(1/upper_bound(y), 1/lower_bound(y))
    return mul_interval(x, reciprocal_y)

Use Ok to unlock and test your code:

python3 ok -q div_interval -u
python3 ok -q div_interval

Q12: Multiple References

Eva Lu Ator, another user, has also noticed the different intervals computed by different but algebraically equivalent expressions. She says that the problem is multiple references to the same interval.

The Multiple References Problem: a formula to compute with intervals using Alyssa's system will produce tighter error bounds if it can be written in such a form that no variable that represents an uncertain number is repeated.

Thus, she says, par2 is a better program for parallel resistances than par1. Is she right? Why? Write a function that returns a string containing a written explanation of your answer:

def multiple_references_explanation():
    return """The multiple reference problem..."""

Q13: Quadratic

Write a function quadratic that returns the interval of all values f(t) such that t is in the argument interval x and f(t) is a quadratic function:

f(t) = a*t*t + b*t + c

Make sure that your implementation returns the smallest such interval, one that does not suffer from the multiple references problem.

Hint: the derivative f'(t) = 2*a*t + b, and so the extreme point of the quadratic is -b/(2*a):

def quadratic(x, a, b, c):
    """Return the interval that is the range of the quadratic defined by
    coefficients a, b, and c, for domain interval x.

    >>> str_interval(quadratic(interval(0, 2), -2, 3, -1))
    '-3 to 0.125'
    >>> str_interval(quadratic(interval(1, 3), 2, -3, 1))
    '0 to 10'
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q quadratic