Homework 5: Object-Oriented Programming, Linked Lists, Trees
Due by 11:59pm on Monday, October 26
Instructions
Download hw05.zip. Inside the archive, you will find a file called
hw05.py, along with a copy of the ok autograder.
Submission: When you are done, submit with python3 ok
--submit. You may submit more than once before the deadline; only the
final submission will be scored. Check that you have successfully submitted
your code on okpy.org. See Lab 0 for more instructions on
submitting assignments.
Using Ok: If you have any questions about using Ok, please refer to this guide.
Readings: You might find the following references useful:
Grading: Homework is graded based on correctness. Each incorrect problem will decrease the total score by one point. There is a homework recovery policy as stated in the syllabus. This homework is out of 2 points.
Required Questions
OOP
Q1: Vending Machine
Create a class called VendingMachine that represents a vending
machine for some product. A VendingMachine object returns strings
describing its interactions.
Fill in the VendingMachine class, adding attributes and methods as
appropriate, such that its behavior matches the following doctests:
class VendingMachine:
"""A vending machine that vends some product for some price.
>>> v = VendingMachine('candy', 10)
>>> v.vend()
'Inventory empty. Restocking required.'
>>> v.add_funds(15)
'Inventory empty. Restocking required. Here is your $15.'
>>> v.restock(2)
'Current candy stock: 2'
>>> v.vend()
'You must add $10 more funds.'
>>> v.add_funds(7)
'Current balance: $7'
>>> v.vend()
'You must add $3 more funds.'
>>> v.add_funds(5)
'Current balance: $12'
>>> v.vend()
'Here is your candy and $2 change.'
>>> v.add_funds(10)
'Current balance: $10'
>>> v.vend()
'Here is your candy.'
>>> v.add_funds(15)
'Inventory empty. Restocking required. Here is your $15.'
>>> w = VendingMachine('soda', 2)
>>> w.restock(3)
'Current soda stock: 3'
>>> w.restock(3)
'Current soda stock: 6'
>>> w.add_funds(2)
'Current balance: $2'
>>> w.vend()
'Here is your soda.'
"""
"*** YOUR CODE HERE ***"
You may find Python string formatting syntax useful. A quick example:
>>> ten, twenty, thirty = 10, 'twenty', [30]
>>> '{0} plus {1} is {2}'.format(ten, twenty, thirty)
'10 plus twenty is [30]'Use Ok to test your code:
python3 ok -q VendingMachineQ2: Mint
Complete the Mint and Coin classes so that the coins created by a mint have
the correct year and worth.
- Each
Mintinstance has ayearstamp. Theupdatemethod sets theyearstamp to thecurrent_yearclass attribute of theMintclass. - The
createmethod takes a subclass ofCoinand returns an instance of that class stamped with themint's year (which may be different fromMint.current_yearif it has not been updated.) - A
Coin'sworthmethod returns thecentsvalue of the coin plus one extra cent for each year of age beyond 50. A coin's age can be determined by subtracting the coin's year from thecurrent_yearclass attribute of theMintclass.
class Mint:
"""A mint creates coins by stamping on years.
The update method sets the mint's stamp to Mint.current_year.
>>> mint = Mint()
>>> mint.year
2020
>>> dime = mint.create(Dime)
>>> dime.year
2020
>>> Mint.current_year = 2100 # Time passes
>>> nickel = mint.create(Nickel)
>>> nickel.year # The mint has not updated its stamp yet
2020
>>> nickel.worth() # 5 cents + (80 - 50 years)
35
>>> mint.update() # The mint's year is updated to 2100
>>> Mint.current_year = 2175 # More time passes
>>> mint.create(Dime).worth() # 10 cents + (75 - 50 years)
35
>>> Mint().create(Dime).worth() # A new mint has the current year
10
>>> dime.worth() # 10 cents + (155 - 50 years)
115
>>> Dime.cents = 20 # Upgrade all dimes!
>>> dime.worth() # 20 cents + (155 - 50 years)
125
"""
current_year = 2020
def __init__(self):
self.update()
def create(self, kind):
"*** YOUR CODE HERE ***"
def update(self):
"*** YOUR CODE HERE ***"
class Coin:
def __init__(self, year):
self.year = year
def worth(self):
"*** YOUR CODE HERE ***"
class Nickel(Coin):
cents = 5
class Dime(Coin):
cents = 10Use Ok to test your code:
python3 ok -q MintLinked Lists
Q3: Store Digits
Write a function store_digits that takes in an integer n and returns
a linked list where each element of the list is a digit of n.
Note: do not use any string manipulation functions like
strandreversed
def store_digits(n):
"""Stores the digits of a positive number n in a linked list.
>>> s = store_digits(1)
>>> s
Link(1)
>>> store_digits(2345)
Link(2, Link(3, Link(4, Link(5))))
>>> store_digits(876)
Link(8, Link(7, Link(6)))
>>> # a check for restricted functions
>>> import inspect, re
>>> cleaned = re.sub(r"#.*\\n", '', re.sub(r'"{3}[\s\S]*?"{3}', '', inspect.getsource(store_digits)))
>>> print("Do not use str or reversed!") if any([r in cleaned for r in ["str", "reversed"]]) else None
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q store_digitsExtra Questions
Trees
Q4: Is BST
Write a function is_bst, which takes a Tree t and returns True if, and
only if, t is a valid binary search tree, which means that:
- Each node has at most two children (a leaf is automatically a valid binary search tree)
- The children are valid binary search trees
- For every node, the entries in that node's left child are less than or equal to the label of the node
- For every node, the entries in that node's right child are greater than the label of the node
An example of a BST is:
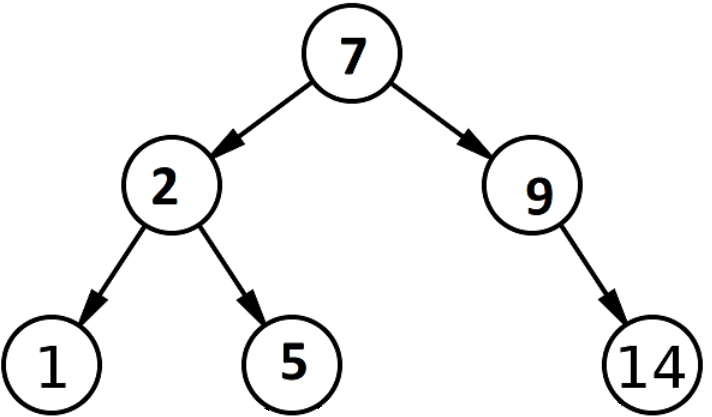
Note that, if a node has only one child, that child could be considered either the left or right child. You should take this into consideration.
Hint: It may be helpful to write helper functions bst_min and bst_max that
return the minimum and maximum, respectively, of a Tree if it is a valid binary
search tree.
def is_bst(t):
"""Returns True if the Tree t has the structure of a valid BST.
>>> t1 = Tree(6, [Tree(2, [Tree(1), Tree(4)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t1)
True
>>> t2 = Tree(8, [Tree(2, [Tree(9), Tree(1)]), Tree(3, [Tree(6)]), Tree(5)])
>>> is_bst(t2)
False
>>> t3 = Tree(6, [Tree(2, [Tree(4), Tree(1)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t3)
False
>>> t4 = Tree(1, [Tree(2, [Tree(3, [Tree(4)])])])
>>> is_bst(t4)
True
>>> t5 = Tree(1, [Tree(0, [Tree(-1, [Tree(-2)])])])
>>> is_bst(t5)
True
>>> t6 = Tree(1, [Tree(4, [Tree(2, [Tree(3)])])])
>>> is_bst(t6)
True
>>> t7 = Tree(2, [Tree(1, [Tree(5)]), Tree(4)])
>>> is_bst(t7)
False
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q is_bstQ5: Preorder
Define the function preorder, which takes in a tree as an argument and
returns a list of all the entries in the tree in the order that
print_tree would print them.
The following diagram shows the order that the nodes would get printed, with the arrows representing function calls.
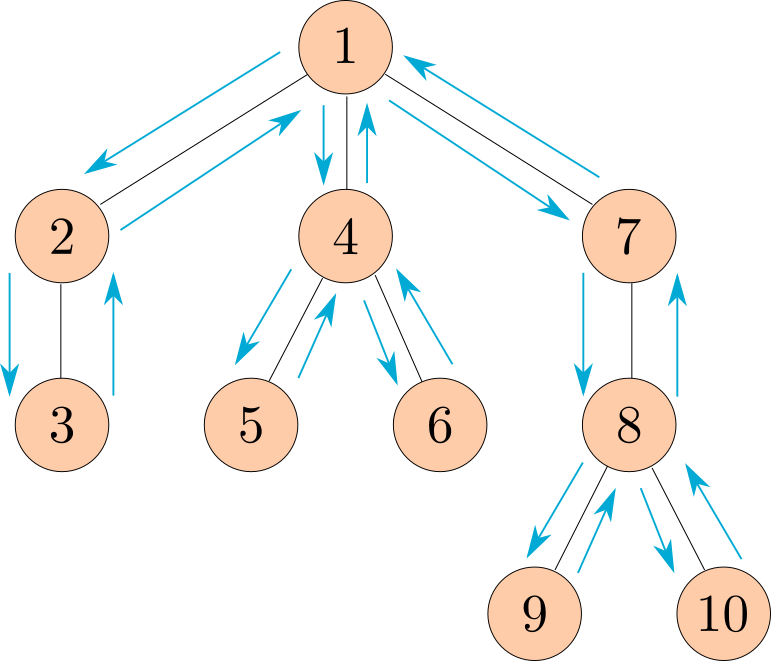
Note: This ordering of the nodes in a tree is called a preorder traversal.
def preorder(t):
"""Return a list of the entries in this tree in the order that they
would be visited by a preorder traversal (see problem description).
>>> numbers = Tree(1, [Tree(2), Tree(3, [Tree(4), Tree(5)]), Tree(6, [Tree(7)])])
>>> preorder(numbers)
[1, 2, 3, 4, 5, 6, 7]
>>> preorder(Tree(2, [Tree(4, [Tree(6)])]))
[2, 4, 6]
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q preorderGenerators/Trees
Q6: Yield Paths
Define a generator function path_yielder which takes in a Tree t, a value
value, and returns a generator object which yields each path from the root of t
to a node that has label value.
t is implemented with a class, not as the function-based ADT.
Each path should be represented as a list of the labels along that path in the tree. You may yield the paths in any order.
We have provided a (partial) skeleton for you. You do not need to use this skeleton, but if your implementation diverges significantly from it, you might want to think about how you can get it to fit the skeleton.
def path_yielder(t, value):
"""Yields all possible paths from the root of t to a node with the label value
as a list.
>>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4, [Tree(6)]), Tree(5)]), Tree(5)])
>>> print(t1)
1
2
3
4
6
5
5
>>> next(path_yielder(t1, 6))
[1, 2, 4, 6]
>>> path_to_5 = path_yielder(t1, 5)
>>> sorted(list(path_to_5))
[[1, 2, 5], [1, 5]]
>>> t2 = Tree(0, [Tree(2, [t1])])
>>> print(t2)
0
2
1
2
3
4
6
5
5
>>> path_to_2 = path_yielder(t2, 2)
>>> sorted(list(path_to_2))
[[0, 2], [0, 2, 1, 2]]
"""
"*** YOUR CODE HERE ***"
for _______________ in _________________:
for _______________ in _________________:
"*** YOUR CODE HERE ***"
Hint: If you're having trouble getting started, think about how you'd approach this problem if it wasn't a generator function. What would your recursive calls be? With a generator function, what happens if you make a "recursive call" within its body?
Use Ok to test your code:
python3 ok -q path_yielder