Lab 4: Recursion, Tree Recursion, Python Lists
Due by 11:59pm on Tuesday, September 22.
Starter Files
Download lab04.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.
Topics
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the questions and refer back here should you get stuck.
Recursion
A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:
- Base case(s), the simplest possible form of the problem you're trying to solve.
- Recursive case(s), where the function calls itself with a simpler argument as part of the computation.
- Using the recursive calls to solve the full problem.
Let's look at the canonical example, factorial.
Factorial, denoted with the
!operator, is defined as:n! = n * (n-1) * ... * 1For example,
5! = 5 * 4 * 3 * 2 * 1 = 120
The recursive implementation for factorial is as follows:
def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)We know from its definition that 0! is 1. Since n == 0 is the smallest number we
can compute the factorial of, we use it as our base case.
The recursive step also follows from the definition of factorial, i.e., n! =
n * (n-1)!.
The next few questions in lab will have you writing recursive functions. Here are some general tips:
- Paradoxically, to write a recursive function, you must assume that the function is fully functional before you finish writing it; this is called the recursive leap of faith.
- Consider how you can solve the current problem using the solution to a simpler version of the problem. The amount of work done in a recursive function can be deceptively little: remember to take the leap of faith and trust the recursion to solve the slightly smaller problem without worrying about how.
- Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you're missing base cases (this is a common way recursive solutions fail).
- It may help to write an iterative version first.
Tree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
A classic example of a tree recursion function is finding the nth Fibonacci number:
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 1) + fib(n - 2)Calling fib(6) results in the following call structure (where f is fib):

Each f(i) node represents a recursive call to fib. Each recursive call
makes another two recursive calls. f(0) and f(1) do not make any recursive
calls because they are the base cases of the function. Because of these base
cases, we are able to terminate the recursion and beginning accumulating the
values.
Generally, tree recursion is effective when you want to explore multiple possibilities or choices at a single step. In these types of problems, you make a recursive call for each choice or for a group of choices. Here are some examples:
- Given a list of paid tasks and a limited amount of time, which tasks should you choose to maximize your pay? This is actually a variation of the Knapsack problem, which focuses on finding some optimal combination of different items.
- Suppose you are lost in a maze and see several different paths. How do you find your way out? This is an example of path finding, and is tree recursive because at every step, you could have multiple directions to choose from that could lead out of the maze.
- Your dryer costs $2 per cycle and accepts all types of coins. How many different combinations of coins can you create to run the dryer? This is similar to the partitions problem from the textbook.
Lists
Lists are Python data structures that can store multiple values. Each value can be any type and can even be another list! A list is written as a comma separated list of expressions within square brackets:
>>> list_of_nums = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]Each element in a list is assigned an index. Lists are zero-indexed, meaning
their indices start at 0 and increase in sequential order. To retrieve an element
from a list, use list indexing:
>>> lst = [6, 5, 4, 3, 2, 1]
>>> lst[0]
6
>>> lst[3]
3Often times we need to know how long a list is when we're working with it. To find
the length of a list, call the function len on it:
>>> len([])
0
>>> len([2, 4, 6, 8, 10])
5Tip: Recall that empty lists,
[], are false-y values. Therefore, you can use an if statement like the following if you only want to do operations on non-empty lists:if lst: # Do stuff with the elements of listThis is equivalent to:
if len(lst) > 0: # Do stuff
You can also create a copy of some portion of the list using list slicing. To slice
a list, use this syntax: lst[<start index>:<end index>]. This expression
evaluates to a new list containing the elements of lst starting at and including
the element at <start index> up to but not including the element at end index.
>>> lst = [True, False, True, True, False]
>>> lst[1:4]
[False, True, True]
>>> lst[:3] # Start index defaults to 0
[True, False, True]
>>> lst[3:] # End index defaults to len(lst)
[True, False]
>>> lst[:] # Creates a copy of the whole list
[True, False, True, True, False]Required Questions
Lists Practice
Q1: List Indexing
Use Ok to test your knowledge with the following "List Indexing" questions:
python3 ok -q list-indexing -u
For each of the following lists, what is the list indexing expression that evaluates to
7? For example, if x = [7], then the answer would be x[0]. You can use the
interpreter or Python Tutor to experiment with your answers. If the code would cause an error, type Error.
>>> x = [1, 3, [5, 7], 9]
______x[2][1]
>>> x = [[3, [5, 7], 9]]
______x[0][1][1]What would Python display? If you get stuck, try it out in the Python interpreter!
>>> lst = [3, 2, 7, [84, 83, 82]]
>>> lst[4]
______Error
>>> lst[3][0]
______84Recursion
Q2: Skip Add
Write a function skip_add that takes a single argument n and computes the
sum of every other integer between 0 and n. Assume n is non-negative.
this_file = __file__
def skip_add(n):
""" Takes a number n and returns n + n-2 + n-4 + n-6 + ... + 0.
>>> skip_add(5) # 5 + 3 + 1 + 0
9
>>> skip_add(10) # 10 + 8 + 6 + 4 + 2 + 0
30
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(this_file, 'skip_add',
... ['While', 'For'])
True
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q skip_addQ3: Summation
Now, write a recursive implementation of summation, which takes a positive
integer n and a function term. It applies term to every number from 1
to n including n and returns the sum of the results.
def summation(n, term):
"""Return the sum of the first n terms in the sequence defined by term.
Implement using recursion!
>>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
225
>>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
54
>>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
62
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(this_file, 'summation',
... ['While', 'For'])
True
"""
assert n >= 1
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q summationTree Recursion
Q4: Insect Combinatorics
Consider an insect in an M by N grid. The insect starts at the
bottom left corner, (0, 0), and wants to end up at the top right
corner, (M-1, N-1). The insect is only capable of moving right or
up. Write a function paths that takes a grid length and width
and returns the number of different paths the insect can take from the
start to the goal. (There is a closed-form solution to this problem,
but try to answer it procedurally using recursion.)
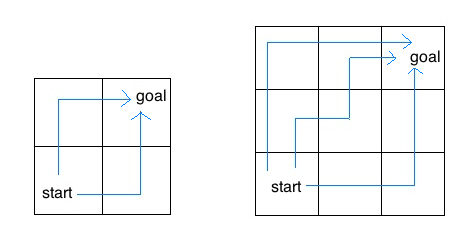
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q pathsQ5: Maximum Subsequence
A subsequence of a number is a series of (not necessarily contiguous) digits of the number. For example, 12345 has subsequences that include 123, 234, 124, 245, etc. Your task is to get the maximum subsequence below a certain length.
def max_subseq(n, t):
"""
Return the maximum subsequence of length at most t that can be found in the given number n.
For example, for n = 20125 and t = 3, we have that the subsequences are
2
0
1
2
5
20
21
22
25
01
02
05
12
15
25
201
202
205
212
215
225
012
015
025
125
and of these, the maxumum number is 225, so our answer is 225.
>>> max_subseq(20125, 3)
225
>>> max_subseq(20125, 5)
20125
>>> max_subseq(20125, 6) # note that 20125 == 020125
20125
>>> max_subseq(12345, 3)
345
>>> max_subseq(12345, 0) # 0 is of length 0
0
>>> max_subseq(12345, 1)
5
"""
"*** YOUR CODE HERE ***"
There are two key insights for this problem:
- You need to split into the cases where the ones digit is used and the one where it is not. In the case where it is, we want to reduce
tsince we used one of the digits, and in the case where it isn't we do not. - In the case where we are using the ones digit, you need to put the digit back onto the end, and the way to attach a digit
dto the end of a numbernis10 * n + d.
Use Ok to test your code:
python3 ok -q max_subseqSubmit
Make sure to submit this assignment by running:
python3 ok --submitOptional Questions
While "Add Characters" is optional, it is good practice for the Cats project and is thus highly recommended!
Q6: Add Characters
Given two words, w1 and w2, we say w1 is a subsequence of w2
if all the letters in w1 appear in w2 in the same order (but
not necessarily all together). That is, you can add letters to any position in
w1 to get w2.
For example, "sing" is a substring of "absorbing" and "cat" is a substring of
"contrast".
Implement add_chars, which takes in w1 and w2, where w1 is a substring of w2. This means that w1 is shorter than w2. It should
return a string containing the characters you need to add to w1 to get w2. Your solution
must use recursion.
In the example above, you need to add the characters "aborb" to "sing" to get "absorbing", and you need to add "ontrs" to "cat" to get "contrast".
The letters in the string you return should be in the order you have to add them from left to right.
If there are multiple characters in the w2 that could correspond to characters in w1, use the
leftmost one. For example, add_words("coy", "cacophony") should return "acphon", not "caphon"
because the first "c" in "coy" corresponds to the first "c" in "cacophony".
def add_chars(w1, w2):
"""
Return a string containing the characters you need to add to w1 to get w2.
You may assume that w1 is a subsequence of w2.
>>> add_chars("owl", "howl")
'h'
>>> add_chars("want", "wanton")
'on'
>>> add_chars("rat", "radiate")
'diae'
>>> add_chars("a", "prepare")
'prepre'
>>> add_chars("resin", "recursion")
'curo'
>>> add_chars("fin", "effusion")
'efuso'
>>> add_chars("coy", "cacophony")
'acphon'
>>> from construct_check import check
>>> # ban iteration and sets
>>> check(LAB_SOURCE_FILE, 'add_chars',
... ['For', 'While', 'Set', 'SetComp']) # Must use recursion
True
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q add_chars