Due by 11:59pm on Thursday, October 14

Instructions

Download hw05.zip. Inside the archive, you will find a file called hw05.py, along with a copy of the ok autograder.

Submission: When you are done, submit with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be scored. Check that you have successfully submitted your code on okpy.org. See Lab 0 for more instructions on submitting assignments.

Using Ok: If you have any questions about using Ok, please refer to this guide.

Readings: You might find the following references useful:

• Section 4.2

Grading: Homework is graded based on correctness. Each incorrect problem will decrease the total score by one point. There is a homework recovery policy as stated in the syllabus. This homework is out of 2 points.

Required Questions

Important: Update (10/11): These questions use the function-based data abstraction tree. If your downloaded hw refers to the Tree object class, that should also be ok in terms of the autograder. If you'd like to see the updated version however, please redownload the zip and copy over your current progress. The Tree class will be covered on Friday, so not quite yet! Feel free to let us know on Piazza if you have any questions.

Q1: Generate Permutations

Given a sequence of unique elements, a permutation of the sequence is a list containing the elements of the sequence in some arbitrary order. For example, [2, 1, 3], [1, 3, 2], and [3, 2, 1] are some of the permutations of the sequence [1, 2, 3].

Implement gen_perms, a generator function that takes in a sequence seq and returns a generator that yields all permutations of seq. For this question, assume that seq will not be empty.

Permutations may be yielded in any order. Note that the doctests test whether you are yielding all possible permutations, but not in any particular order. The built-in sorted function takes in an iterable object and returns a list containing the elements of the iterable in non-decreasing order.

Hint: If you had the permutations of all the elements in seq not including the first element, how could you use that to generate the permutations of the full seq?

Hint: Remember, it's possible to loop over generator objects because generators are iterators!

def gen_perms(seq):
    """Generates all permutations of the given sequence. Each permutation is a
    list of the elements in SEQ in a different order. The permutations may be
    yielded in any order.

    >>> perms = gen_perms([100])
    >>> type(perms)
    <class 'generator'>
    >>> next(perms)
    [100]
    >>> try: #this piece of code prints "No more permutations!" if calling next would cause an error
    ...     next(perms)
    ... except StopIteration:
    ...     print('No more permutations!')
    No more permutations!
    >>> sorted(gen_perms([1, 2, 3])) # Returns a sorted list containing elements of the generator
    [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
    >>> sorted(gen_perms((10, 20, 30)))
    [[10, 20, 30], [10, 30, 20], [20, 10, 30], [20, 30, 10], [30, 10, 20], [30, 20, 10]]
    >>> sorted(gen_perms("ab"))
    [['a', 'b'], ['b', 'a']]
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q gen_perms
Copy
✂️

Q2: Yield Paths

Define a generator function path_yielder which takes in a tree t, a value value, and returns a generator object which yields each path from the root of t to a node that has label value.

Each path should be represented as a list of the labels along that path in the tree. You may yield the paths in any order.

We have provided a skeleton for you. You do not need to use this skeleton, but if your implementation diverges significantly from it, you might want to think about how you can get it to fit the skeleton.

def path_yielder(t, value):
    """Yields all possible paths from the root of t to a node with the label
    value as a list.

    >>> t1 = tree(1, [tree(2, [tree(3), tree(4, [tree(6)]), tree(5)]), tree(5)])
    >>> print_tree(t1)
    1
      2
        3
        4
          6
        5
      5
    >>> next(path_yielder(t1, 6))
    [1, 2, 4, 6]
    >>> path_to_5 = path_yielder(t1, 5)
    >>> sorted(list(path_to_5))
    [[1, 2, 5], [1, 5]]

    >>> t2 = tree(0, [tree(2, [t1])])
    >>> print_tree(t2)
    0
      2
        1
          2
            3
            4
              6
            5
          5
    >>> path_to_2 = path_yielder(t2, 2)
    >>> sorted(list(path_to_2))
    [[0, 2], [0, 2, 1, 2]]
    """
    "*** YOUR CODE HERE ***"
    for _______________ in _________________:
        for _______________ in _________________:
            "*** YOUR CODE HERE ***"

Hint: If you're having trouble getting started, think about how you'd approach this problem if it wasn't a generator function. What would your recursive calls be? With a generator function, what happens if you make a "recursive call" within its body?

Hint: Remember, it's possible to loop over generator objects because generators are iterators!

Note: Remember that this problem should yield items -- do not return a list!

Use Ok to test your code:

python3 ok -q path_yielder
Copy
✂️

Q3: Preorder

Define the function preorder, which takes in a tree as an argument and returns a list of all the entries in the tree in the order that print_tree would print them.

The following diagram shows the order that the nodes would get printed, with the arrows representing function calls.

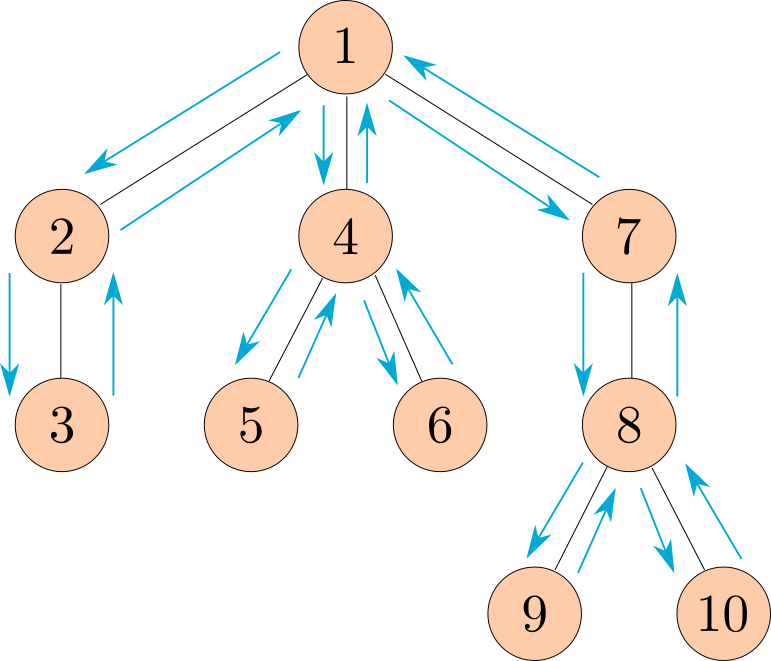
Note: This ordering of the nodes in a tree is called a preorder traversal.

def preorder(t):
    """Return a list of the entries in this tree in the order that they
    would be visited by a preorder traversal (see problem description).

    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> preorder(numbers)
    [1, 2, 3, 4, 5, 6, 7]
    >>> preorder(tree(2, [tree(4, [tree(6)])]))
    [2, 4, 6]
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q preorder
Copy
✂️

Q4: Generate Preorder

Similarly to preorder in Question 3, define the function generate_preorder, which takes in a tree as an argument and now instead yields the entries in the tree in the order that print_tree would print them.

Hint: How can you modify your implementation of preorder to yield from your recursive calls instead of returning them?

def generate_preorder(t):
    """Yield the entries in this tree in the order that they
    would be visited by a preorder traversal (see problem description).

    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> gen = generate_preorder(numbers)
    >>> next(gen)
    1
    >>> list(gen)
    [2, 3, 4, 5, 6, 7]
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q generate_preorder
Copy
✂️

Extra Questions

Q5: Remainder Generator

Like functions, generators can also be higher-order. For this problem, we will be writing remainders_generator, which yields a series of generator objects.

remainders_generator takes in an integer m, and yields m different generators. The first generator is a generator of multiples of m, i.e. numbers where the remainder is 0. The second is a generator of natural numbers with remainder 1 when divided by m. The last generator yields natural numbers with remainder m - 1 when divided by m.

Hint: To create a generator of infinite natural numbers, you can call the naturals function that's provided in the starter code.

Hint: Consider defining an inner generator function. Each yielded generator varies only in that the elements of each generator have a particular remainder when divided by m. What does that tell you about the argument(s) that the inner function should take in?

def remainders_generator(m):
    """
    Yields m generators. The ith yielded generator yields natural numbers whose
    remainder is i when divided by m.

    >>> import types
    >>> [isinstance(gen, types.GeneratorType) for gen in remainders_generator(5)]
    [True, True, True, True, True]
    >>> remainders_four = remainders_generator(4)
    >>> for i in range(4):
    ...     print("First 3 natural numbers with remainder {0} when divided by 4:".format(i))
    ...     gen = next(remainders_four)
    ...     for _ in range(3):
    ...         print(next(gen))
    First 3 natural numbers with remainder 0 when divided by 4:
    4
    8
    12
    First 3 natural numbers with remainder 1 when divided by 4:
    1
    5
    9
    First 3 natural numbers with remainder 2 when divided by 4:
    2
    6
    10
    First 3 natural numbers with remainder 3 when divided by 4:
    3
    7
    11
    """
    "*** YOUR CODE HERE ***"

Note that if you have implemented this correctly, each of the generators yielded by remainder_generator will be infinite - you can keep calling next on them forever without running into a StopIteration exception.

Use Ok to test your code:

python3 ok -q remainders_generator
Copy
✂️