Discussion 4: Tree Recursion, Python Lists
Tree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
For example, let's say we want to recursively calculate the
nth
Virahanka-Fibonacci number,
defined as:
def virfib(n):
if n == 0 or n == 1:
return n
return virfib(n - 1) + virfib(n - 2)Calling virfib(6) results in the following call structure that looks like
an upside-down tree (where f is virfib):
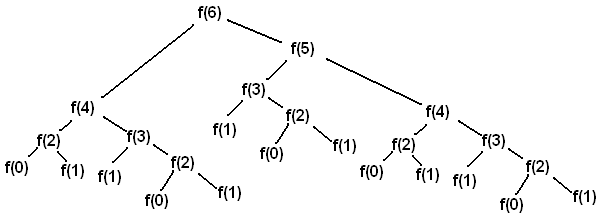
Each f(i) node represents a recursive call to virfib.
Each recursive call f(i) makes another two recursive calls,
which are to f(i-1) and f(i-2).
Whenever we reach a f(0) or f(1) node, we can directly return 0 or 1
rather than making more recursive calls, since these are our base cases.
In other words, base cases have the information needed to return an answer directly, without depending upon results from other recursive calls. Once we've reached a base case, we can then begin returning back from the recursive calls that led us to the base case in the first place.
Generally, tree recursion can be effective for problems where there are multiple possibilities or choices at a current state. In these types of problems, you make a recursive call for each choice or for a group of choices.
Q1: Count Stair Ways
Imagine that you want to go up a flight of stairs that has n steps,
where n is a positive integer.
You can either take 1 or 2 steps each time. How many different ways can you go up this flight of stairs?
In this question, you'll write a function count_stair_ways that solves this problem.
Before you code your approach, consider these questions.
How many different ways are there to go up a flight of stairs with n = 1 step? How about n = 2 steps? Try writing out some other examples and see if you notice any patterns.
What’s the base case for this question? What is the simplest input?
What do count_stair_ways(n - 1) and count_stair_ways(n - 2) represent?
Fill in the code for count_stair_ways:
Q2: Count K
Consider a special version of the count_stair_ways problem, where instead of taking 1 or 2 steps, we are able to take up to and including k steps at a time. Write a function count_k that figures out the number of paths for this scenario. Assume n and k are positive.
Run in 61A CodeHint: Your solution will follow a very similar logic to what you did for
count_stair_ways.
Lists
A list is a data structure that can store multiple elements. Each element can be of any type, even a list itself. We write a list as a comma-separated list of expressions in square brackets:
>>> list_of_ints = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]Each element in the list has an index, with the index of the first element
starting at 0. We say that lists are therefore "zero-indexed."
With list indexing, we can specify the index of the element we want to retrieve.
A negative index represents starting from the end of the list, so the
negative index -i is equivalent to the positive index len(lst)-i.
>>> lst = [6, 5, 4, 3, 2, 1, 0]
>>> lst[0]
6
>>> lst[3]
3
>>> lst[-1] # Same as lst[6]
0List slicing
To create a copy of part or all of a list, we can use list slicing.
The syntax to slice a list lst is:
lst[<start index>:<end index>:<step size>].
This expression evaluates to a new list containing the elements of lst:
- Starting at and including the element at
<start index>. - Up to but not including the element at
<end index>. - With
<step size>as the difference between indices of elements to include.
If the start, end, or step size are not explicitly specified, Python has default values for them. A negative step size indicates that we are stepping backwards through a list when including elements.
>>> lst[:3] # Start index defaults to 0
[6, 5, 4]
>>> lst[3:] # End index defaults to len(lst)
[3, 2, 1, 0]
>>> lst[::-1] # Make a reversed copy of the entire list
[0, 1, 2, 3, 4, 5, 6]
>>> lst[::2] # Skip every other; step size defaults to 1 otherwise
[6, 4, 2, 0]List comprehensions
List comprehensions are a compact and powerful way of creating new lists out of sequences. The general syntax for a list comprehension is the following:
[<expression> for <element> in <sequence> if <conditional>]where the if <conditional> section is optional.
The syntax is designed to read like English: "Compute the expression for each element in the sequence (if the conditional is true for that element)."
>>> [i**2 for i in [1, 2, 3, 4] if i % 2 == 0]
[4, 16]This list comprehension will:
- Compute the expression
i**2 - For each element
iin the sequence[1, 2, 3, 4] - Where
i % 2 == 0(iis an even number),
and then put the resulting values of the expressions into a new list.
In other words, this list comprehension will create a new list that contains
the square of every even element of the original list [1, 2, 3, 4].
We can also rewrite a list comprehension as an equivalent for statement,
such as for the example above:
>>> lst = []
>>> for i in [1, 2, 3, 4]:
... if i % 2 == 0:
... lst = lst + [i**2]
>>> lst
[4, 16]Q3: WWPD: Lists
What would Python display?
>>> a = [1, 5, 4, [2, 3], 3]
>>> print(a[0], a[-1])>>>len(a)>>> 2 in a>>> a[3][0]Q4: Even weighted
Write a function that takes a list s and returns a new list that keeps only
the even-indexed elements of s and multiplies them by their corresponding
index.
Q5: Max Product
Write a function that takes in a list and returns the maximum product that can be formed using nonconsecutive elements of the list. The input list will contain only numbers greater than or equal to 1.
Run in 61A CodeDictionaries
Dictionaries are data structures which map keys to values. Dictionaries in Python are unordered, unlike real-world dictionaries --- in other words, key-value pairs are not arranged in the dictionary in any particular order. Let's look at an example:
>>> pokemon = {'pikachu': 25, 'dragonair': 148, 'mew': 151}
>>> pokemon['pikachu']
25
>>> pokemon['jolteon'] = 135
>>> pokemon
{'jolteon': 135, 'pikachu': 25, 'dragonair': 148, 'mew': 151}
>>> pokemon['ditto'] = 25
>>> pokemon
{'jolteon': 135, 'pikachu': 25, 'dragonair': 148,
'ditto': 25, 'mew': 151}The keys of a dictionary can be any immutable value, such as numbers, strings, and tuples.[1] Dictionaries themselves are mutable; we can add, remove, and change entries after creation. There is only one value per key, however --- if we assign a new value to the same key, it overrides any previous value which might have existed.
To access the value of dictionary at key, use the syntax
dictionary[key].
Element selection and reassignment work similarly to sequences, except the square brackets contain the key, not an index.
[1]To be exact, keys must be hashable, which is out of scope for this course. This means that some mutable objects, such as classes, can be used as dictionary keys.
Q6: WWPD: Dictionaries
What would Python display?
>>> pokemon = {'pikachu': 25, 'dragonair': 148}
>>> pokemon>>> 'mewtwo' in pokemon>>> len(pokemon)>>> pokemon['mew'] = pokemon['pikachu']
>>> pokemon[25] = 'pikachu'
>>> pokemon>>> pokemon['mewtwo'] = pokemon['mew'] * 2
>>> pokemon>>> pokemon[['firetype', 'flying']] = 146Note that the last example demonstrates that dictionaries cannot use other mutable data structures as keys. However, dictionaries can be arbitrarily deep, meaning the values of a dictionary can be themselves dictionaries.