Discussion 8: Linked Lists, Mutable Trees, Efficiency
Representation: Repr, Str
Q1: WWPD: Repr-esentation
Note: This is not the typical way
repris used, nor is this way of writingreprrecommended, this problem is mainly just to make sure you understand howreprandstrwork.
class A:
def __init__(self, x):
self.x = x
def __repr__(self):
return self.x
def __str__(self):
return self.x * 2
class B:
def __init__(self):
print('boo!')
self.a = []
def add_a(self, a):
self.a.append(a)
def __repr__(self):
print(len(self.a))
ret = ''
for a in self.a:
ret += str(a)
return retGiven the above class definitions, what will the following lines output?
>>> A('one')>>> print(A('one'))>>> repr(A('two'))>>> b = B()>>> b.add_a(A('a'))
>>> b.add_a(A('b'))
>>> bLinked Lists
There are many different implementations of sequences in Python. Today, we'll explore the linked list implementation.
A linked list is either an empty linked list, or a Link object containing a
first value and the rest of the linked list.
To check if a linked list is an empty linked list, compare it against the class
attribute Link.empty:
if link is Link.empty:
print('This linked list is empty!')
else:
print('This linked list is not empty!')You can find an implementation of the Link class below:
class Link:
"""A linked list."""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __repr__(self):
if self.rest:
rest_repr = ', ' + repr(self.rest)
else:
rest_repr = ''
return 'Link(' + repr(self.first) + rest_repr + ')'
def __str__(self):
string = '<'
while self.rest is not Link.empty:
string += str(self.first) + ' '
self = self.rest
return string + str(self.first) + '>'Q2: The Hy-rules of Linked Lists
In this question, we are given the following Linked List:
ganondorf = Link('zelda', Link('link', Link('sheik', Link.empty)))What expression would give us the value 'sheik' from this Linked List?
What is the value of ganondorf.rest.first?
What would be the value of str(ganondorf)?
What expression would mutate this linked list to <zelda ganondorf sheik>?
Q3: Sum Nums
Write a function that takes in a linked list and returns the sum of all
its elements. You may assume all elements in s are integers. Try to implement this recursively!
Q4: Multiply Links
Write a function that takes in a Python list of linked lists and multiplies them element-wise. It should return a new linked list.
If not all of the Link objects are of equal length, return a
linked list whose length is that of the shortest linked list given. You
may assume the Link objects are shallow linked lists, and that
lst_of_lnks contains at least one linked list.
Q5: Flip Two
Write a recursive function flip_two that takes as input a
linked list s and mutates s so that every pair
is flipped.
Trees
We define a tree to be a recursive data abstraction that has a label (the value stored in the root of the tree) and branches (a list of trees directly underneath the root). Previously, we implemented the tree abstraction using Python lists. Let's look at another implementation using objects instead:
class Tree:
def __init__(self, label, branches=[]):
for b in branches:
assert isinstance(b, Tree)
self.label = label
self.branches = branches
def is_leaf(self):
return not self.branchesWith this implementation, we can mutate a tree using attribute assignment, which wasn't possible in the previous implementation using lists. That's why we sometimes call these objects "mutable trees."
>>> t = Tree(3, [Tree(4), Tree(5)])
>>> t.label = 5
>>> t.label
5Q6: Make Even
Define a function make_even which takes in a tree
t whose values are integers, and mutates the tree such that all the
odd integers are increased by 1 and all the even integers remain the same.
Q7: Add Leaves
Implement add_d_leaves, a function that takes in a Tree instance t and a number v.
We define the depth of a node in t to be the number of edges from the root to that node. The depth of root is therefore 0.
For each node in the tree, you should add d leaves to it, where d is the depth of the node. Every added leaf should have a label of v. If the node at this depth has existing branches, you should add these leaves to the end of that list of branches.
For example, you should be adding 1 leaf with label v to each node at depth 1, 2 leaves to each node at depth 2, and so on.
Here is an example of a tree t(shown on the left) and the result after add_d_leaves is applied with v as 5.
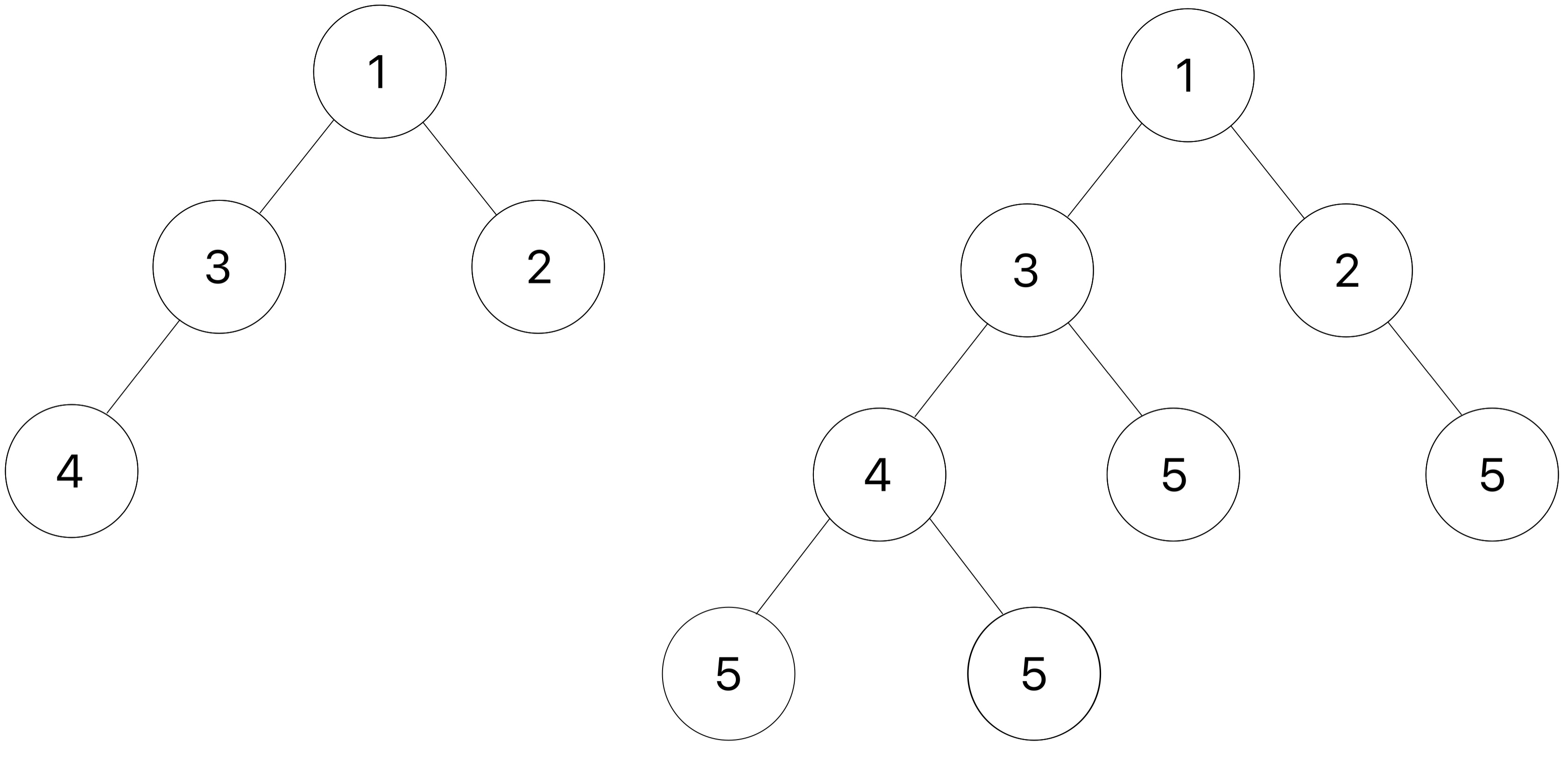
Try drawing out the second doctest to visualize how the function is mutating
t3.
Run in 61A CodeHint: Use a helper function to keep track of the depth!
Efficiency (Orders of Growth)
When we talk about the efficiency of a function, we are often interested in the following: as the size of the input grows, how does the runtime of the function change? And what do we mean by runtime?
Example 1: square(1) requires one primitive operation: multiplication.
square(100) also requires one. No matter what input n we pass into square, it always takes a constant number of operations (1). In other words, this function has a runtime complexity of Θ(1).
As an illustration, check out the table below:
| input | function call | return value | operations |
|---|---|---|---|
| 1 | square(1) |
1*1 | 1 |
| 2 | square(2) |
2*2 | 1 |
| ... | ... | ... | ... |
| 100 | square(100) |
100*100 | 1 |
| ... | ... | ... | ... |
| n | square(n) |
n*n | 1 |
Example 2: factorial(1) requires one multiplication, but factorial(100) requires 100 multiplications. As we increase the input size of n, the runtime (number of operations) increases linearly proportional to the input. In other words, this function has a runtime complexity of Θ(n).
As an illustration, check out the table below:
| input | function call | return value | operations |
|---|---|---|---|
| 1 | factorial(1) |
1*1 | 1 |
| 2 | factorial(2) |
2*1*1 | 2 |
| ... | ... | ... | ... |
| 100 | factorial(100) |
100*99*...*1*1 | 100 |
| ... | ... | ... | ... |
| n | factorial(n) |
n*(n-1)*...*1*1 | n |
Example 3: Consider the following function:
def bar(n):
for a in range(n):
for b in range(n):
print(a,b)bar(1) requires 1 print statements, while bar(100) requires 100*100 = 10000 print statements (each time a increments, we have 100 print statements due to the inner for loop). Thus, the runtime increases quadratically proportional to the input. In other words, this function has a runtime complexity of Θ(n^2).
| input | function call | operations (prints) |
|---|---|---|
| 1 | bar(1) |
1 |
| 2 | bar(2) |
4 |
| ... | ... | ... |
| 100 | bar(100) |
10000 |
| ... | ... | ... |
| n | bar(n) |
n^2 |
Example 4: Consder the following function:
def rec(n):
if n == 0:
return 1
else:
return rec(n - 1) + rec(n - 1)rec(1) requires one addition, as it returns rec(0) + rec(0), and rec(0) hits the base case and requires no further additions. but rec(4) requires 2^4 - 1 = 15 additions. To further understand the intuition, we can take a look at the recurisve tree below. To get rec(4), we need one addition. We have two calls to rec(3), which each require one addition, so this level needs two additions. Then we have four calls to rec(2), so this level requires four additions, and so on down the tree. In total, this adds up to 1 + 2 + 4 + 8 = 15 additions.
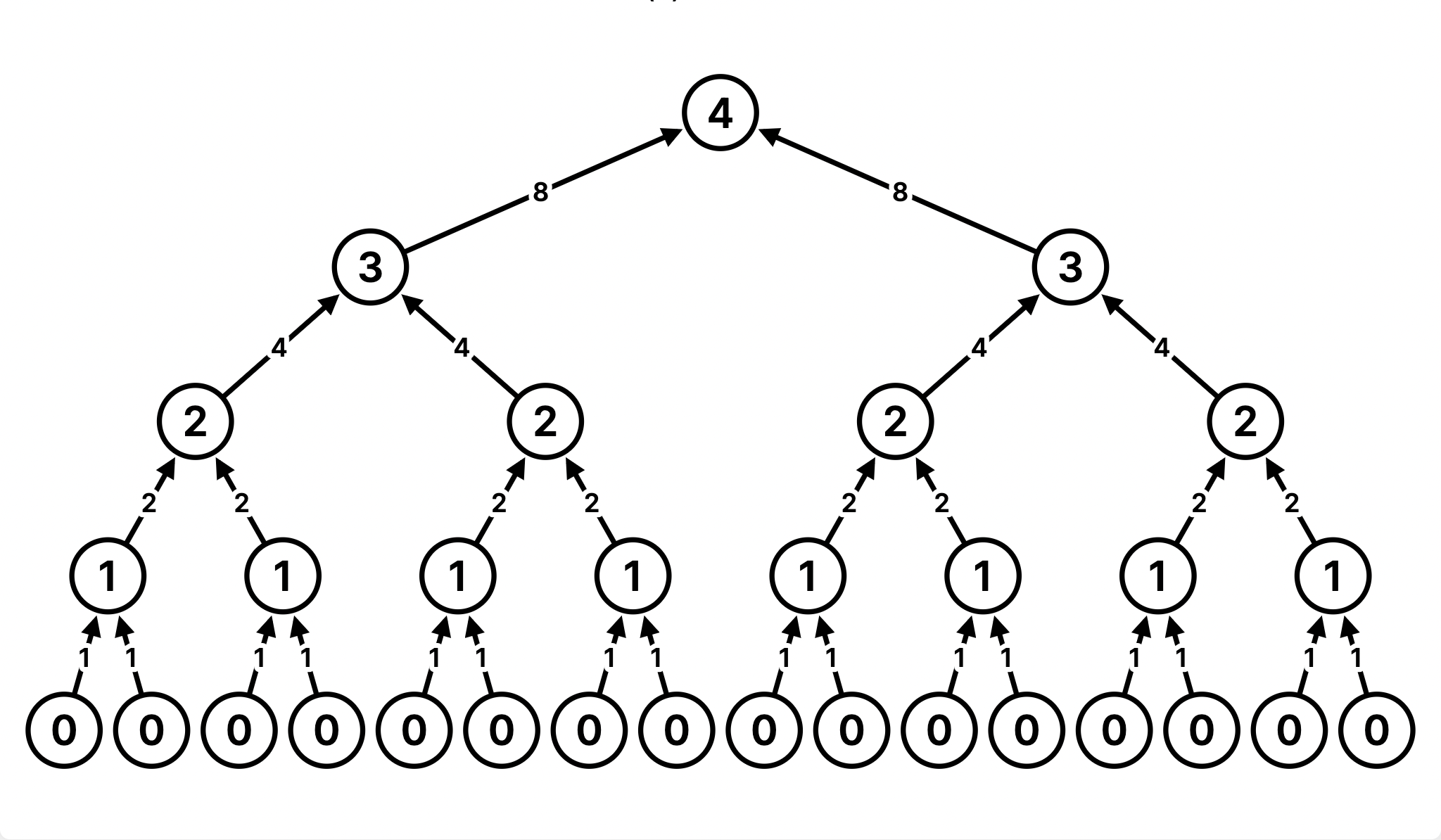
As we increase the input size of n, the runtime (number of operations) increases exponentially proportional to the input. In other words, this function has a runtime complexity of Θ(2^n).
As an illustration, check out the table below:
| input | function call | return value | operations |
|---|---|---|---|
| 1 | rec(1) |
2 | 1 |
| 2 | rec(2) |
4 | 3 |
| ... | ... | ... | ... |
| 10 | rec(10) |
1024 | 1023 |
| ... | ... | ... | ... |
| n | rec(n) |
2^n |
2^n |
Here are some general guidelines for finding the order of growth for the runtime of a function:
If the function is recursive or iterative, you can subdivide the problem as seen above:
- Count the number of recursive calls/iterations that will be made in terms of input size
n. - Find how much work is done per recursive call or iteration in terms of input size
n. - The answer is usually the product of the above two, but be sure to pay attention to control flow!
- Count the number of recursive calls/iterations that will be made in terms of input size
- If the function calls helper functions that are not constant-time, you need to take the runtime of the helper functions into consideration.
- We can ignore constant factors. For example
1000000nandnsteps are both linear. - We can also ignore smaller factors. For example if
hcallsfandg, andfis Quadratic whilegis linear, thenhis Quadratic. For the purposes of this class, we take a fairly coarse view of efficiency. All the problems we cover in this course can be grouped as one of the following:
- Constant: the amount of time does not change based on the input size. Rule:
n --> 2nmeanst --> t. - Logarithmic: the amount of time changes based on the logarithm of the input size. Rule:
n --> 2nmeanst --> t + k. - Linear: the amount of time changes with direct proportion to the size of the input. Rule:
n --> 2nmeanst --> 2t. - Quadratic: the amount of time changes based on the square of the input size. Rule:
n --> 2nmeanst --> 4t. - Exponential: the amount of time changes with a power of the input size. Rule:
n --> n + 1meanst --> 2t.
- Constant: the amount of time does not change based on the input size. Rule:
Q8: WWPD: Orders of Growth
What is the worst case (i.e. when n is prime) order of growth of is_prime in terms of n?
def is_prime(n):
for i in range(2, n):
if n % i == 0:
return False
return TrueChoose one of:
- Constant
- Logarithmic
- Linear
- Quadratic
- Exponential
- None of these
What is the order of growth of bar in terms of n?
def bar(n):
i, sum = 1, 0
while i <= n:
sum += biz(n)
i += 1
return sum
def biz(n):
i, sum = 1, 0
while i <= n:
sum += i**3
i += 1
return sumChoose one of:
- Constant
- Logarithmic
- Linear
- Quadratic
- Exponential
- None of these
What is the order of growth of foo in terms of n, where n is the length
of lst? Assume that slicing a list and calling len on a list can both be
done in constant time. Write your answer in Θ notation.
def foo(lst, i):
mid = len(lst) // 2
if mid == 0:
return lst
elif i > 0:
return foo(lst[mid:], -1)
else:
return foo(lst[:mid], 1)