61A Homework 3
Note the special due date and time: Due by 7pm on Tuesday, 2/12
Submission. See the online submission instructions. We have provided a starter file for the questions below.
Readings. Section 1.6 and 1.7 of the online lecture notes.
Q1. The idea of smoothing a function is an important concept in signal processing. If f is a one-argument function and dx is some small number, then the smoothed version of f is the function whose value at a point x is the average of f(x - dx), f(x), and f(x + dx). Write a function smooth that takes as input a function f and a value to use for dx and returns a function that computes the smoothed version of f. Do not use any def statements inside of smooth; use lambda expressions instead.
def smooth(f, dx):
"""Returns the smoothed version of f, g where
g(x) = (f(x - dx) + f(x) + f(x + dx)) / 3
>>> square = lambda x: x ** 2
>>> round(smooth(square, 1)(0), 3)
0.667
"""
"*** YOUR CODE HERE ***"
It is sometimes valuable to repeatedly smooth a function (that is, smooth the smoothed function, and so on) to obtain the n-fold smoothed function. Show how to generate the n-fold smoothed function, n_fold_smooth, of any given function using your smooth function and repeated from homework 2. As with smooth, use lambda expressions rather than def statements in the body of n_fold_smooth.
def n_fold_smooth(f, dx, n):
"""Returns the n-fold smoothed version of f
>>> square = lambda x: x ** 2
>>> round(n_fold_smooth(square, 1, 3)(0), 3)
2.0
"""
"*** YOUR CODE HERE ***"
Q2. An infinite continued fraction is an expression of the form:
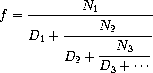
As an example, one can show that the inverse of the golden ratio can be computed by setting all of the terms to 1. A way to approximate the value of an infinite continued fraction is to compute the value of truncating after a given number of terms. This truncation, called the k-term finite continued fraction, has the form:
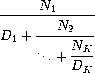
Write a function iterative_continued_frac, which takes two functions n_term and d_term, which each produce the ith N and D term respectively, and a number k and returns the k-term finite continued fraction. Use iteration to perform the computation.
def iterative_continued_frac(n_term, d_term, k):
"""Returns the k-term continued fraction with numerators defined by n_term
and denominators defined by d_term.
>>> # golden ratio
... round(iterative_continued_frac(lambda x: 1, lambda x: 1, 8), 3)
0.618
>>> # 1 / (1 + (2 / (2 + (3 / (3 + (4 / 4))))))
... round(iterative_continued_frac(lambda x: x, lambda x: x, 4), 6)
0.578947
"""
"*** YOUR CODE HERE ***"
Now write a function recursive_continued_frac that uses recursion to compute the k-term finite continued fraction. Hint: try writing a recursive helper function to do most of the work, rather than trying to do the recursion with recursive_continued_frac directly.
def recursive_continued_frac(n_term, d_term, k):
"""Returns the k-term continued fraction with numerators defined by n_term
and denominators defined by d_term.
>>> # golden ratio
... round(recursive_continued_frac(lambda x: 1, lambda x: 1, 8), 3)
0.618
>>> # 1 / (1 + (2 / (2 + (3 / (3 + (4 / 4))))))
... round(recursive_continued_frac(lambda x: x, lambda x: x, 4), 6)
0.578947
"""
"*** YOUR CODE HERE ***"
Q3. A mathematical function G on positive integers is defined by two cases:
G(n) = n, if n <= 3
G(n) = G(n - 1) + 2 * G(n - 2) + 3 * G(n - 3), if n > 3
Write a recursive function g that computes G(n). Then, write an iterative function g_iter that computes G(n):
def g(n):
"""Return the value of G(n), computed recursively.
>>> g(1)
1
>>> g(2)
2
>>> g(3)
3
>>> g(4)
10
>>> g(5)
22
"""
"*** YOUR CODE HERE ***"
def g_iter(n):
"""Return the value of G(n), computed iteratively.
>>> g_iter(1)
1
>>> g_iter(2)
2
>>> g_iter(3)
3
>>> g_iter(4)
10
>>> g_iter(5)
22
"""
"*** YOUR CODE HERE ***"
Q4. (Extra for experts) The recursive factorial function can be written as a single expression by using a conditional expression.
>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1))) >>> fact(5) 120
However, this implementation relies on the fact (no pun intended) that fact has a name, to which we refer in the body of fact. To write a recursive function, we have always given it a name using a def or assignment statement so that we can refer to the function within its own body. In this question, your job is to define fact without giving it a name!
Write an expression that computes n factorial using only call expressions, conditional expressions, and lambda expressions (no assignment or def statements). The sub and mul functons from the operator module are the only built-in function required to solve this problem. Return the expression from the function below:
from operator import sub, mul
def make_anonymous_factorial():
"""Return the value of an expression that computes factorial.
>>> make_anonymous_factorial()(5)
120
"""
return YOUR_EXPRESSION_HERE