You can get the starter file like this: cp ~cs61a/lib/lab/lab09/lab9.scm .
Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses Polish-prefix notation and (often many) nested parenthesis. (See: http://xkcd.com/297/). Odd as the syntax may seem, it allows us to write, with relative ease, something very beautiful, called a metacircular evaluator. We will see this later in the course. Scheme also features first-class functions and optimized tail-recursion, which were relatively new features at the time.
Enough with all this talk though; let's see some code. You may interact with the Scheme interpeter by typing stk on a terminal of one of the instructional machines.
We have primitives...
STk> 1 1 STk> "word" "word" STk> 'symbol symbol STk> #t #t
And we have functions.
STk> + #[closure arglist=args 196920] STk> (+ 1 2) 3 STk> (+ (* 1 1) 2) 3
Notice that to call a function we need to enclose it in parenthesis, with its arguments following. Syntax for other familiar programming constructs follow this format. (Can you see why it is very easy to translate this syntax into trees? Try drawing out trees for a few instructions)
STk> (if (> 1 0) 1 2) 1 STk> (define (square x) (* x x)) square STk> (square 3) 9 STk> (define square (lambda (x) (* x x))) square STk> (square 3) 9 STk> (define x (cons 1 (cons 2 '()))) x STk> (car x) 1 STk> (car (cdr x)) 2 # What do cons, car, and cdr remind you of?
Here we have seen if expressions, function definitions, lambdas, name binding, list constructing, and list selecting. Of course there are many other things Scheme can do. For a useful (but not exhaustive) list of Scheme primitive functions, see this.
Predict what will happen and then try it out. Make sure you understand what is happening! Remember, despite the different syntax, Scheme is just another programming language, like Python.
3
(+ 2 3)
(+ 5 6 7 8)
(+)
(sqrt 16)
(+ (* 3 4) 5)
+
'+
'hello
'(+ 2 3)
'(good morning)
(first 274)
(butfirst 274)
(first 'hello)
(first hello)
(first (bf 'hello))
(+ (first 23) (last 45))
(define pi 3.14159)
pi
'pi
(+ pi 7)
(* pi pi)
(define (square x) (* x x))
(square 5)
(square (+ 2 3))
(define a 3)
(define b (+ a 1))
(+ a b (* a b))
(= a b)
(if (and (> b a) (< b (* a b)))
b
a)
(cond ((= a 4) 6)
((= b 4) (+ 6 7 a))
(else 25))
(+ 2 (if (> b a) b a))
(* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1))
((if (< a b) + -) a b)
Finally, just as in Python, you can load a Scheme file and interact with its definitions. Simply, type "stk -load filename.scm". Alternatively, enter stk and type (load "filename.scm"). You may exit the interpreter by typing Ctrl-D, (bye), or (exit).
Note: many of the following problems will be taken from SICP, a famous and influential introductory computer science book from MIT.
Another Note: if you have any questions on syntax, please try to look it up yourself before asking your TA. One of the hopes of this course is that you are exposed to the main ideas in programming. Once you understand the key concepts, different languages should be easy to pick up. Many features in Python have an analogue in Scheme; they just look different.
To familiarize ourselves with Scheme, let us revisit a familiar problem: factorial. We will write it using a recursive procedure, but with both recursive and iterative processes. Read section 1.2.1 of this link to see what we mean by this. In short, an iterative process is summarized by state variables (for example, a counter and a sum), and update and termination rules. The iterative process can still use an underlying recursive procedure.
1.) Write factorial with a recursive process.
2.) Write factorial with an iterative process (the procedure should still make a recursive call!).
In the iterative case, most programming languages consume memory proportional to the number of procedure calls. However, Scheme "will execute an iterative process in constant space, even if the iterative process is described by a recursive procedure. An implementation with this property is called tail-recursive." We see then that syntax such as "for" and "while" loops are not necessary in Scheme; they are merely "syntactic sugar".
In Scheme, functions are first-class, meaning they can be passed around just like any other data type. In particular, this means more higher order function fun.
1.) A common numerical calculation we use computers to approximate is integration. Simpson's rule is one such approximation method. It is given by the formula below.
h/3 * [y0 + 4y1 + 2y2 + 4y3 ... + 2yn-2 + 4yn-1 + yn]
where h = (b-a)/n, n is even, and yk = f(a + kh).
Implement a function that takes in f, a, b, and n, and returns the approximation of the integration of f given by Simpson's Rule. Test this out with the cube function between 0 and 1, with n equal to 100. You should get 0.25. Hint: sum (a function we provide) and let (a Scheme feature) may be useful. (Exercise 1.29 SICP)
2.) Write a function product analogous to sum, that returns the product of values of a function over a range. Write it recursively and iteratively. (Exercise 1.31 SICP)
3.) As you may have noticed, sum and product are both specific versions of general accumulator functions. Write an accumulate function with the following function signature:
(accumulate combiner null-value term a next b)
Define sum and product in terms of accumulate. (Exercise 1.32 SICP)
The main data structure of Scheme is the humble pair! From this, we can form a myriad of structures, including as you hopefully noticed above, Rlists. To create a pair, we use cons. To get the first we use car, and to get the rest we use cdr. The symbol '() represents the empty Rlist.
1.) Create the structure in the picture below. Check that your solution is correct!
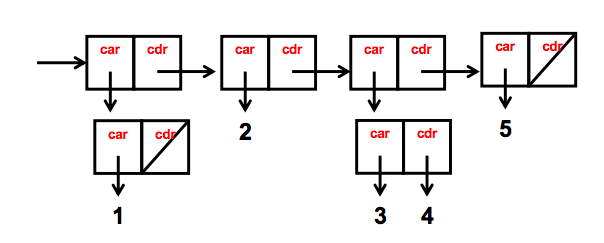
2.) Implement a function (interleave lst1 lst2) that interleaves two lists.
3.) Implement a function (remove item lst) that takes in a list and returns a new list with item removed from lst.
4.) Implement a function (all_satisfies lst pred) that returns #t iff all of the elements in the list satisfy pred.
5.) Implement a function (repeat_els pred lst) that repeats all elements in the lst that satisfy pred. Use HOFs.