61A Homework 5
Due by 11:59pm on Tuesday, 3/11
Submission. See the online submission instructions. We have provided a hw5.py starter file for the questions below.
Q1. Define a function reverse_list that takes a list as an argument and returns None, but reverses the elements in the list as a side effect. Do not use any built-in list methods (especially not reverse) or slicing, but element assignment statements are fine:
def reverse_list(s):
"""Reverse the contents of list s and return None.
>>> digits = [6, 2, 9, 5, 1, 4, 1, 3]
>>> reverse_list(digits)
>>> digits
[3, 1, 4, 1, 5, 9, 2, 6]
>>> d = digits
>>> reverse_list(d)
>>> digits
[6, 2, 9, 5, 1, 4, 1, 3]
"""
"*** YOUR CODE HERE ***"
Hint: This question was also asked in discussion 5, so you get a freebie. You should try to implement it on your own before looking up the answer, though!
Q2. Define a function shuffle that takes a list with an even number of elements (cards) and creates a new list that interleaves the elements of the first half with the elements of the second half:
def card(n):
"""Return the playing card type for a positive n <= 13."""
assert type(n) == int and n > 0 and n <= 13, "Bad card n"
specials = {1: 'A', 11: 'J', 12: 'Q', 13: 'K'}
return specials.get(n, str(n))
def shuffle(cards):
"""Return a shuffled list that interleaves the two halves of cards.
>>> suits = ['♡', '♢', '♤', '♧']
>>> cards = [card(n) + suit for n in range(1,14) for suit in suits]
>>> cards[:12]
['A♡', 'A♢', 'A♤', 'A♧', '2♡', '2♢', '2♤', '2♧', '3♡', '3♢', '3♤', '3♧']
>>> cards[26:30]
['7♤', '7♧', '8♡', '8♢']
>>> shuffle(cards)[:12]
['A♡', '7♤', 'A♢', '7♧', 'A♤', '8♡', 'A♧', '8♢', '2♡', '8♤', '2♢', '8♧']
>>> shuffle(shuffle(cards))[:12]
['A♡', '4♢', '7♤', '10♧', 'A♢', '4♤', '7♧', 'J♡', 'A♤', '4♧', '8♡', 'J♢']
>>> cards[:12] # Should not be changed
['A♡', 'A♢', 'A♤', 'A♧', '2♡', '2♢', '2♤', '2♧', '3♡', '3♢', '3♤', '3♧']
"""
assert len(cards) % 2 == 0, 'len(cards) must be even'
"*** YOUR CODE HERE ***"
Q3. A graph in computer science refers to a structure such as this.
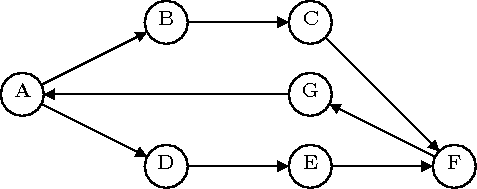
The circles are called vertices (singular vertex) and the lines joining vertices are called edges. The letters in the vertices are vertex labels.
This particular graph is directed, meaning that the edges have a direction (shown by the arrows). We say that a directed graph is cyclic if there is a path constructed from edges that leads from some vertex back to itself. For example, the sample graph is cyclic because, among other examples, one can follow edges from A->B->C->F->G->A.
If we identify the vertices of a graph by their labels, then we can represent a graph as a dictionary mapping each vertex label L to a list successor vertices' labels (vertices at the other ends of arrows pointing out of L). Thus, the sample graph would be:
G = { 'A': ['B', 'D'], 'B': ['C'], 'C': ['F'], 'D': ['E'],
'E': ['F'], 'F': ['G'], 'G': ['A'] }
Dag Hacker has developed the following program to determine if a graph represented in this fashion is circular:
def is_circular(G):
"""Return true iff G represents a circular directed graph."""
for v in G:
if reaches_circularity(G, v):
return True
return False
def reaches_circularity(G, v0):
"""Returns true if there is a circularity in G in some path
starting from vertex V0."""
def is_path_to_cycle(v1):
for w in G[v1]:
if v0 == w:
return True
if is_path_to_cycle(w):
return True
return False
return is_path_to_cycle(v0)
Unfortunately, his reaches_circularity function does not always work. It gives correct answers on acyclic graphs (graphs that are not cyclic), but often goes into infinite loops on cyclic ones. Fill in the program below to fix Dag's problem:
def reaches_circularity(G, v0):
"""Returns true if there is a circularity in G in some path
starting from vertex V0.
>>> G = { 'A': ['B', 'D'], 'B': ['C'], 'C': ['F'], 'D': ['E'],
... 'E': ['F'], 'F': ['G'], 'G': ['A'] }
>>> is_circular(G)
True
>>> G['F'] = []
>>> is_circular(G)
False
"""
"*** YOUR CODE HERE ***"
Hint: The problem has to do with what happens if there is a cycle in a path that starts at vertex v, but does not include v itself.
Q4. In lecture, we saw how to use functions to create mutable objects. Here, for example, is the function, make_withdraw, which produces a function that can withdraw money from an account:
def make_withdraw(balance):
"""Return a withdraw function with BALANCE as its starting balance.
>>> withdraw = make_withdraw(1000)
>>> withdraw(100)
900
>>> withdraw(100)
800
>>> withdraw(900)
'Insufficient funds'
"""
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
Write a version of the make_withdraw function that returns password-protected withdraw functions. That is, make_withdraw should take a password argument (a string) in addition to an initial balance. The returned function should take two arguments: an amount to withdraw and a password.
A password-protected withdraw function should only process withdrawals that include a password that matches the original. Upon receiving an incorrect password, the function should:
- Store that incorrect password in a list, and
- Return the string 'Incorrect password'.
If a withdraw function has been called three times with incorrect passwords p1, p2, and p3, then it is locked. All subsequent calls to the function should return:
"Your account is locked. Attempts: [<p1>, <p2>, <p3>]"
The incorrect passwords may be the same or different:
def make_withdraw(balance, password):
"""Return a password-protected withdraw function.
>>> w = make_withdraw(100, 'hax0r')
>>> w(25, 'hax0r')
75
>>> w(90, 'hax0r')
'Insufficient funds'
>>> w(25, 'hwat')
'Incorrect password'
>>> w(25, 'hax0r')
50
>>> w(75, 'a')
'Incorrect password'
>>> w(10, 'hax0r')
40
>>> w(20, 'n00b')
'Incorrect password'
>>> w(10, 'hax0r')
"Your account is locked. Attempts: ['hwat', 'a', 'n00b']"
>>> w(10, 'l33t')
"Your account is locked. Attempts: ['hwat', 'a', 'n00b']"
"""
"*** YOUR CODE HERE ***"
Q5. Suppose that our banking system requires the ability to make joint accounts. Define a function make_joint that takes three arguments.
- A password-protected withdraw function,
- The password with which that withdraw function was defined, and
- A new password that can also access the original account.
The make_joint function returns a withdraw function that provides additional access to the original account using either the new or old password. Both functions draw down the same balance. Incorrect passwords provided to either function will be stored and cause the functions to be locked after three wrong attempts.
Hint: The solution is short (less than 10 lines) and contains no string literals! The key is to call withdraw with the right password and interpret the result. You may assume that all failed attempts to withdraw will return some string (for incorrect passwords, locked accounts, or insufficient funds), while successful withdrawals will return a number.
Use type(value) == str to test if some value is a string:
def make_joint(withdraw, old_password, new_password):
"""Return a password-protected withdraw function that has joint access to
the balance of withdraw.
>>> w = make_withdraw(100, 'hax0r')
>>> w(25, 'hax0r')
75
>>> make_joint(w, 'my', 'secret')
'Incorrect password'
>>> j = make_joint(w, 'hax0r', 'secret')
>>> w(25, 'secret')
'Incorrect password'
>>> j(25, 'secret')
50
>>> j(25, 'hax0r')
25
>>> j(100, 'secret')
'Insufficient funds'
>>> j2 = make_joint(j, 'secret', 'code')
>>> j2(5, 'code')
20
>>> j2(5, 'secret')
15
>>> j2(5, 'hax0r')
10
>>> j2(25, 'password')
'Incorrect password'
>>> j2(5, 'secret')
"Your account is locked. Attempts: ['my', 'secret', 'password']"
>>> j(5, 'secret')
"Your account is locked. Attempts: ['my', 'secret', 'password']"
>>> w(5, 'hax0r')
"Your account is locked. Attempts: ['my', 'secret', 'password']"
>>> make_joint(w, 'hax0r', 'hello')
"Your account is locked. Attempts: ['my', 'secret', 'password']"
"""
"*** YOUR CODE HERE ***"
ALL FOLLOWING QUESTIONS ARE EXTRA FOR EXPERTS (OPTIONAL)
Section 2.4.8 describes a system for solving equations with multiple free parameters using constraint programming, a declarative style of programming that asserts constraints and then applies a general method of constraint satisfaction. The following questions ask you to extend that system. The code for the system appears at the end of this homework.
Q6. (Extra for experts) Implement the function triangle_area, which defines a relation among three connectors, the base b, height h, and area a of a triangle, so that a = 0.5 * b * h:
def triangle_area(a, b, h):
"""Connect a, b, and h so that a is the area of a triangle with base b and
height h.
>>> a, b, h = [connector(n) for n in ('area', 'base', 'height')]
>>> triangle_area(a, b, h)
>>> a['set_val']('user', 75.0)
area = 75.0
>>> b['set_val']('user', 15.0)
base = 15.0
height = 10.0
"""
"*** YOUR CODE HERE ***"
Q7. (Extra for experts) The multiplier constraint from the readings is insufficient to model equations that include squared quantities because constraint networks must not include loops. Implement a new constraint squarer that represents the squaring relation:
def squarer(a, b):
"""The constraint that a*a=b.
>>> x, y = connector('X'), connector('Y')
>>> s = squarer(x, y)
>>> x['set_val']('user', 10)
X = 10
Y = 100
>>> x['forget']('user')
X is forgotten
Y is forgotten
>>> y['set_val']('user', 16)
Y = 16
X = 4.0
"""
"*** YOUR CODE HERE ***"
Q8. (Extra for experts) Use your squarer constraint to build a constraint network for the Pythagorean theorem: a squared plus b squared equals c squared:
def pythagorean(a, b, c):
"""Connect a, b, and c into a network for the Pythagorean theorem:
a*a + b*b = c*c
>>> a, b, c = [connector(name) for name in ('A', 'B', 'C')]
>>> pythagorean(a, b, c)
>>> a['set_val']('user', 5)
A = 5
>>> c['set_val']('user', 13)
C = 13
B = 12.0
"""
"*** YOUR CODE HERE ***"
Here is the equation solver implementation from the readings:
def connector(name=None):
"""A connector between constraints.
>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')
>>> converter(celsius, fahrenheit)
>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0
>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212
>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten
>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0
"""
informant = None # The source of the current val
constraints = [] # A list of connected constraints
def set_value(source, value):
nonlocal informant
val = connector['val']
if val is None:
informant, connector['val'] = source, value
if name is not None:
print(name, '=', value)
inform_all_except(source, 'new_val', constraints)
else:
if val != value:
print('Contradiction detected:', val, 'vs', value)
def forget_value(source):
nonlocal informant
if informant == source:
informant, connector['val'] = None, None
if name is not None:
print(name, 'is forgotten')
inform_all_except(source, 'forget', constraints)
connector = {'val': None,
'set_val': set_value,
'forget': forget_value,
'has_val': lambda: connector['val'] is not None,
'connect': lambda source: constraints.append(source)}
return connector
def inform_all_except(source, message, constraints):
"""Inform all constraints of the message, except source."""
for c in constraints:
if c != source:
c[message]()
def ternary_constraint(a, b, c, ab, ca, cb):
"""The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b)=a."""
def new_value():
av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
if av and bv:
c['set_val'](constraint, ab(a['val'], b['val']))
elif av and cv:
b['set_val'](constraint, ca(c['val'], a['val']))
elif bv and cv:
a['set_val'](constraint, cb(c['val'], b['val']))
def forget_value():
for connector in (a, b, c):
connector['forget'](constraint)
constraint = {'new_val': new_value, 'forget': forget_value}
for connector in (a, b, c):
connector['connect'](constraint)
return constraint
from operator import add, sub, mul, truediv
def adder(a, b, c):
"""The constraint that a + b = c."""
return ternary_constraint(a, b, c, add, sub, sub)
def multiplier(a, b, c):
"""The constraint that a * b = c."""
return ternary_constraint(a, b, c, mul, truediv, truediv)
def constant(connector, value):
"""The constraint that connector = value."""
constraint = {}
connector['set_val'](constraint, value)
return constraint
def converter(c, f):
"""Connect c to f to convert from Celsius to Fahrenheit."""
u, v, w, x, y = [connector() for _ in range(5)]
multiplier(c, w, u)
multiplier(v, x, u)
adder(v, y, f)
constant(w, 9)
constant(x, 5)
constant(y, 32)