
We've provided a set of starter files with skeleton code for the exercises in the lab. You can get them in the following places:
Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses Polish-prefix notation and (often many) nested parenthesis. (See: http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.
Let's take a look at the primitives in Scheme. Open up the Scheme
interpreter in your terminal with the command stk, and try typing in
the following expressions to see what Scheme would print.
STk> 1 ; Anything following a ';' is a comment
?
STk> 1.0
?
STk> -27
?
STk> #t ; True
?
STk> #f ; False
?
STk> "A string"
?
STk> 'symbol
?
STk> nil
()
Of course, what kind of programming language would Scheme be if it
didn't have any functions? Scheme uses Polish prefix notation, where
the operator comes before the operands. For example, to evaluate 3 +
4, we would type into the Scheme interpreter:
STk> (+ 3 4)
Notice that to call a function we need to enclose it in parenthesis,
with its arguments following. Be careful about this, as while in
Python an extra set of parentheses won't hurt, in Scheme, it will
interpret the parentheses as a function call. Evaluating (3) results
in an error because Scheme tries to call a function called 3 that
takes no arguments, which would result in an error.
Let's familiarize ourselves with some of the built-in functions in Scheme. Try out the following in the interpreter
STk> (+ 3 5)
?
STk> (- 10 4)
?
STk> (* 7 6)
?
STk> (/ 28 2)
?
STk> (+ 1 2 3 4 5 6 7 8 9) ;Arithmetic operators allow a variable number of arguments
?
STk> (abs -7) ;Absolute Value
?
STk> (quotient 29 5)
?
STk> (remainder 29 5)
?
STk> (= 1 3)
?
STk> (> 1 3)
?
STk> (< 1 3)
?
STk> (or #t #f)
?
STk> (and #t #t)
?
STk> (and #t #f (/ 1 0)) ;Short-Circuiting
?
STk> (not #t)
?
STk> (define x 3) ;Defining Variables
STk> x
?
STk> (define y (+ x 4))
STk> y
?
STk> nil
?
To write a program, we need to write functions, so let's define one. The syntax for defining a program in Scheme is:
(define ([name] [args])
[body])
For example, let's define the double function:
(define (double x)
(+ x x))
Try it yourself! Define a function which cubes an input. You can load
your definitions into Scheme by entering stk -load filename.scm in
your terminal, or if you have the interpreter already opened up (load
"filename.scm").
(define (cube x)
0) ; Replace the 0 with your code
So far, we can't do much in our functions so let's introduce control statements to allow our functions to do more complex operations! The if-statement has the following format:
(if [condition]
[true_result]
[false_result])
For example, the following code written in Scheme and Python are equivalent:
;Scheme
(if (> x 3)
1
2)
#Python
if x > 3:
1
else:
2
Notice that the if-statement has no elif case. If want to have
multiple cases with the if-statement, you would need multiple branched
if-statements:
;Scheme
(if (< x 0)
(display "Negative")
(if (= x 0)
(display "Zero")
(display "Positive")))
#Python Equivalent
if x < 0:
print('Negative')
else:
if x == 0:
print('Zero')
else:
print('Positive')
But this gets messy as more cases are needed, so alternatively, we
also have the cond statement, which has a different syntax:
(cond ([condition_1] [result_1])
([condition_2] [result_2])
...
([condition_n] [result_n])
(else [result_else])) ;'else' is optional
With this, we can write control statements with multiple cases neatly and without needing branching if-statements.
(cond ((and (> x 0) (= (modulo x 2) 0)) (display "Positive Even Integer"))
((and (> x 0) (= (modulo x 2) 1)) (display "Positive Odd Integer"))
((= x 0) (display "Zero"))
((and (< x 0) (= (modulo x 2) 0)) (display "Negative Even Integer"))
((and (< x 0) (= (modulo x 2) 1)) (display "Negative Odd Integer")))
Now that we have control statements in Scheme, let us revisit a familiar problem: factorial. We will write it using a recursive procedure, but with both recursive and iterative processes. Read section 1.2.1 of this link to see what we mean by this. In short, an iterative process is summarized by state variables (for example, a counter and a sum), and update and termination rules. The iterative process can still use an underlying recursive procedure.
factorial with a recursive process.factorial with an iterative process. The procedure should
still make a recursive call!In the iterative case, most programming languages consume memory proportional to the number of procedure calls. However, Scheme "will execute an iterative process in constant space, even if the iterative process is described by a recursive procedure. An implementation with this property is called tail-recursive." We see then that syntax such as "for" and "while" loops are not necessary in Scheme; they are merely "syntactic sugar".
In Scheme, lists are composed similarly to how Rlists that we had worked with
in Python were implemented. Lists are made up pairs, which can point to two
objects. To create a pair, we use the cons function,
which takes two arguments:
STk> (define a (cons 3 5))
a
STk> a
(3 . 5)
Note the dot between the 3 and 5. The dot indicates that this is a
pair, rather than a sequence (as you'll see in a bit).
To retrive a value from a pair, we use the car and cdr functions
to retrieve the first and second elements in the pair.
STk> (car a)
3
STk> (cdr a)
5
Look familiar yet? Like how Rlists are formed, lists in Scheme are
formed by having the first element of a pair be the first element of
the list, and the second element of the pair point to another pair
containing the rest of list, or to nil to signify the end of the
list. For example, the sequence (1, 2, 3) can be represented in Scheme
with the following line:
STk> (define a (cons 1 (cons 2 (cons 3 nil))))
which creates the following object in Scheme:

We can then of course retrieve values from our list with the car and
cdr function.
STk> a
(1 2 3)
STk> (car a)
1
STk> (cdr a)
(2 3)
STk> (car (cdr (cdr a)))
3
This is not the only way to create a list though. You can also use the
list function, as well as the quote form to form a list as well:
STk> (list 1 2 3)
(1 2 3)
STk> '(1 2 3)
(1 2 3)
STk> '(1 . (2 . (3)))
There are a few other built-in functions in Scheme that are used for lists:
STk> (define a '(1 2 3 4))
a
STk> (define b '(4 5 6))
b
STk> (define empty '())
empty
STk> (append '(1 2 3) '(4 5 6))
(1 2 3 4 5 6)
STk> (length '(1 2 3 4 5))
5
STk> (null? '(1 2 3)) ;Checks whether list is empty.
#f
STk> (null? '())
#t
STk> (null? nil)
#t
Create the structure as defined in the picture below. Check to make sure that your solution is correct!
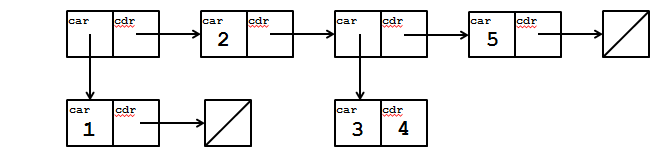
Implement a function (remove item lst) that takes in a list and
returns a new list with item removed from lst.
Create a function (filter f lst), which takes a predicate function
and a list, and returns a new list containing only elements of the
list that satisfy the predicate.
Implement a function (all_satisfies lst pred) that returns #t if all
of the elements in the list satisfy pred.
There's a lot to Scheme, which is perhaps too much for this lab. Scheme takes a bit of time to get used to, but it's really not much different from any other language. The important thing is to just try different things and learn through practice. You can find more exercises here.
We are continuing our journey through the world of interpreters! We have seen interpreters before -- that thing you've been running all of your Python in? That's an interpreter! In fact, the Python interpreter we've been using all semester long is just a program, albeit a very complex one. You can think of it as a program that takes strings as input, evaluates them, and prints the result as output.
There's nothing magical about interpreters, though! They are programs, just like the ones you have been writing throughout the entire semester. In fact, it's possible to write a Python interpreter in Python! However, because Python is a complex language, writing an interpreter for it would be a very daunting project. Today, we'll play around with an interpreter for a calculator language.
In lecture, you were introduced to Calc, which acts as a simple
calculator. You should have already copied the starter files
(scheme_reader.py, calc.py, etc.) at the start of the lab. You can
try running Calc by running this command in the terminal:
python3 calc.py
To exit the program, type Ctrl-D or Ctrl-C.
Trace through the code in calc.py that would be evaluated when you
type the following into calc.
> 2
> (+ 2 3)
> (+ 2 3 4)
> (+ 2 3)
> (+ 2)
> (+ 2 (* 4 5))
While prefix notation (+ 2 3) is easy for computers to interpret,
it's not very natural for humans. We'd much prefer infix notation
(2 + 3). Let's implement this in our own version of calc!
To do this, you need to fill in the following functions, which are in
the scheme_reader.py file.
Implement read_infix. This function takes two arguments: first, the
first expression in the infix expression; and src, the Buffer of
tokens that contains the rest of the infix expression (and possibly
more). For example, if we wanted to construct 3 + 4 5 (note: the 5
will be ignored, so it's really just 3 + 4)), we would call
read_infix(3, Buffer(tokenize_lines('+ 4 5')))
The return value should be an expression which is mathematically the
same as the infix notation expression (e.g. (+ 3 4)), but written
using Scheme style Pairs. See the doctests for simple examples. Follow
these steps:
Buffer. Hint:
the Buffer class in the buffer.py file has a more_on_line
property method. If there aren't, we should just return nil. Also,
we would need to return nil if the Buffer's current value
(there's already a method that gives you the current value!) is
equal to one of two things. Think about what these two things would
be.Implement next_is_op. This function returns True if the next token
in the given Buffer is an operator, and False otherwise.
Hint: don't forget to check if there are any tokens in the buffer
first. Also, don't remove any tokens from the Buffer (i.e. don't use
pop; think of another method you can use).
Modify scheme_read to parse infix expressions. This requires
modifying two parts of the code:
2 + 3. To do this, check if the first item in the Buffer is a
float or a int (this part's already written). If it is, then check
that the next token is an operator. If it is, read it like an infix
expression. (Try to call methods you've already written!)
Otherwise, just return the value (this part's already written).Next, we have to deal with the case of infix notation inside
parentheses. Without parentheses, 2 + 2 * 3 and 2 * 3 + 2 should
produce the exact same result, but in calc, they don't! calc doesn't
implement order of operations, because prefix notation naturally
takes care of operator precedence (why?).
Instead of solving the real problem, we'll implement a quick fix. If
we allow expressions to be surrounded by parentheses, we can write
expressions like 2 + (2 * 3), which will evaluate to the same
thing as (2 * 3) + 2.
To do this, we need to change how we parse lists. This logic should
be very similar to what you did in the previous part of
scheme_read. Hint: The code should be exactly like part 1, but
figure out why!
And that's it! We have infix notation! The following inputs to calc should work.
> (+ 2 2 * 3)
8
> 2 + (- 5 2)
5
> (+ 1 3 * 4 (* 7 4))
41
> (2 * 3) + 6
12
> 6 + (2 * 3)
12
Now we're going to add the ability to define variables. For example:
> (define x 3)
x
> (+ x 2)
5
> (* x (+ 2 x))
15
For this part, we will be modifying the calc.py file. Do we need to
change calc_eval? calc_apply? Is define a special form?
Implement do_define_form. This function takes in a Pair that contains
2 items: the variable name, and the expression to which it should be
assigned. do_define_form should modify the global environment, env
(a dictionary, defined near the top of calc.py) to contain the
name/value binding. It should also return the name of the variable
you're defining.
Finally, implement the lookup procedure in calc_eval. You should
check if the given identifier exp is in the environment. If it is, then
simply return the value associated with it. If not, you should raise an
exception to signal that the user did something wrong.
And that's it! There you have basic variable declaration.