Due at 11:59pm on 03/12/2015.
Download lab07.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
A linked list is either an empty linked list (Link.empty) or a first value
and the rest of the linked list.
class Link:
"""A linked list.
>>> s = Link(1, Link(2, Link(3, Link(4))))
>>> len(s)
4
>>> s[2]
3
>>> s
Link(1, Link(2, Link(3, Link(4))))
"""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __getitem__(self, i):
if i == 0:
return self.first
else:
return self.rest[i-1]
def __len__(self):
return 1 + len(self.rest)
def __repr__(self):
if self.rest is not Link.empty:
rest_str = ', ' + repr(self.rest)
else:
rest_str = ''
return 'Link({0}{1})'.format(repr(self.first), rest_str)To check if a Link is empty, compare it against the class attribute
Link.empty:
if link is Link.empty:
print('This linked list is empty!')Predict what Python will display when the following lines are typed into the interpreter:
>>> Link()
______TypeError
>>> link = Link(1, Link(2, Link(3)))
>>> link.first
______1
>>> link.rest.first
______2
>>> link.rest.rest.rest is Link.empty
______True
>>> link.first = 9001
>>> link.first
______9001
>>> link.rest = link.rest.rest
>>> link.rest.first
______3
>>> link = Link(1)
>>> link.rest = link
>>> link.rest.rest.rest.rest.first
______1Implement a function insert that takes a Link, a value, and an index, and
inserts the value into the Link at the given index. You can assume the linked
list already has at least one element. Do not return anything — insert should
mutate the linked list.
def insert(link, value, index):
"""Insert a value into a Link at the given index.
>>> link = Link(1, Link(2, Link(3)))
>>> insert(link, 9001, 0)
>>> link
Link(9001, Link(1, Link(2, Link(3))))
>>> insert(link, 100, 2)
>>> link
Link(9001, Link(1, Link(100, Link(2, Link(3)))))
>>> insert(link, 4, 5)
Index out of bounds!
"""
"*** YOUR CODE HERE ***"
if index == 0:
link.rest = Link(link.first, link.rest)
link.first = value
elif link.rest is Link.empty:
print('Index out of bounds!')
else:
insert(link.rest, value, index - 1)
# iterative solution
def insert(link, value, index):
while index > 0 and link.rest is not Link.empty:
link = link.rest
index -= 1
if index == 0:
link.rest = Link(link.first, link.rest)
link.first = value
else:
print('Index out of bounds!')As we saw in lecture, we can also represent trees as objects.
class Tree:
def __init__(self, entry, branches=()):
self.entry = entry
for branch in branches:
assert isinstance(branch, Tree)
self.branches = branches
def __repr__(self):
if self.branches:
branches_str = ', ' + repr(self.branches)
else:
branches_str = ''
return 'Tree({0}{1})'.format(self.entry, branches_str)
def is_leaf(self):
return not self.branchesPredict what Python will display when the following lines are typed into the interpreter:
>>> t = Tree(1, Tree(2))
______TypeError
>>> t = Tree(1, [Tree(2)])
>>> t.entry
______1
>>> t.branches[0]
______Tree(2)
>>> t.branches[0].entry
______2
>>> t.entry = t.branches[0].entry
>>> t
______Tree(2, [Tree(2)])
>>> t.branches.append(Tree(4, [Tree(8)]))
>>> len(t.branches)
______2
>>> t.branches[0]
______Tree(2)
>>> t.branches[1]
______Tree(4, [Tree(8)])Write a function square_tree that mutates a Tree with numerical entries so
that each entry is squared.
def square_tree(t):
"""Mutates a Tree t by squaring all its elements.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> square_tree(t)
>>> t
Tree(1, [Tree(9, [Tree(25)]), Tree(49)])
"""
"*** YOUR CODE HERE ***"
t.entry = t.entry ** 2
for subtree in t.branches:
square_tree(subtree)The following questions are for extra practice — they can be found in the lab07_extra.py file. It is recommended that you complete these problems on your own time.
Write a function list_to_link that converts a Python list to a Link.
def list_to_link(lst):
"""Takes a Python list and returns a Link with the same elements.
>>> list_to_link([1, 2, 3])
Link(1, Link(2, Link(3)))
"""
"*** YOUR CODE HERE ***"
if not lst:
return Link.empty
else:
return Link(lst[0], list_to_link(lst[1:]))Write a function link_to_list that converts a given Link to a
Python list.
def link_to_list(link):
"""Takes a Link and returns a Python list with the same elements.
>>> link = Link(1, Link(2, Link(3, Link(4))))
>>> link_to_list(link)
[1, 2, 3, 4]
>>> link_to_list(Link.empty)
[]
"""
"*** YOUR CODE HERE ***"
# Recursive solution
if link is Link.empty:
return []
return [link.first] + link_to_list(link.rest)
# Iterative solution
def link_to_list(link):
result = []
while link is not Link.empty:
result.append(link.first)
link = link.rest
return resultImplement a function reverse that reverses a given Link. reverse should
return a new Link that is the reverse of the original, without modifying the
original.
def reverse(link):
"""Returns a Link that is the reverse of the original.
>>> reverse(Link(1))
Link(1)
>>> link = Link(1, Link(2, Link(3)))
>>> reverse(link)
Link(3, Link(2, Link(1)))
>>> link
Link(1, Link(2, Link(3)))
"""
"*** YOUR CODE HERE ***"
new = Link(link.first)
while link.rest is not Link.empty:
link = link.rest
new = Link(link.first, new)
return newExtra for experts: Implement mutate_reverse, a recursive mutating version
of reverse. Have it mutate the original Link so that its elements are
reversed.
def mutate_reverse(link):
"""Mutates the Link so that its elements are reversed.
>>> link = Link(1)
>>> mutate_reverse(link)
>>> link
Link(1)
>>> link = Link(1, Link(2, Link(3)))
>>> mutate_reverse(link)
>>> link
Link(3, Link(2, Link(1)))
"""
"*** YOUR CODE HERE ***"
if link is Link.empty or link.rest is Link.empty:
return
mutate_reverse(link.rest)
while link.rest is not Link.empty:
link.first, link.rest.first = link.rest.first, link.first
link = link.restWrite a function leaves that returns a list of all the entries of the leaf nodes of a Tree.
def leaves(t):
"""Returns a list of all the entries of the leaf nodes of the Tree t.
>>> leaves(Tree(1))
[1]
>>> leaves(Tree(1, [Tree(2, [Tree(3)]), Tree(4)]))
[3, 4]
"""
"*** YOUR CODE HERE ***"
if t.is_leaf():
return [t.entry]
all_leaves = []
for b in t.branches:
all_leaves += leaves(b)
return all_leavesWrite a function cumulative_sum that returns a new Tree, where each entry is the sum of all entries in the corresponding subtree of the old Tree.
def cumulative_sum(t):
"""Return a new Tree, where each entry is the sum of all entries in the
corresponding subtree of t.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> cumulative = cumulative_sum(t)
>>> t
Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> cumulative
Tree(16, [Tree(8, [Tree(5)]), Tree(7)])
>>> cumulative_sum(Tree(1))
Tree(1)
"""
"*** YOUR CODE HERE ***"
branches = [cumulative_sum(st) for st in t.branches]
new_entry = sum(st.entry for st in branches) + t.entry
return Tree(new_entry, branches)Write a function same_shape that returns True if two Trees have the same
shape. Two trees have the same shape if they have the same number of children
and each of their children have the same shape.
def same_shape(t1, t2):
"""Returns whether two Trees t1, t2 have the same shape. Two trees have the
same shape if they have the same number of branches and each of their
children have the same shape.
>>> t, s = Tree(1), Tree(3)
>>> same_shape(t, t)
True
>>> same_shape(t, s)
True
>>> t = Tree(1, [Tree(2), Tree(3)])
>>> same_shape(t, s)
False
>>> s = cumulative_sum(t)
>>> same_shape(t, s)
True
"""
"*** YOUR CODE HERE ***"
return len(t1.branches) == len(t2.branches) and \
all(same_shape(st1, st2) for st1, st2 in zip(t1.branches, t2.branches))When we write recursive functions acting on Links, we often find
that they have the following form:
def func(link):
if link is Link.empty:
return <Base case>
else:
return <Expression involving func(link.rest)>In the spirit of abstraction, we want to factor out this commonly seen
pattern. It turns out that we can define an abstraction called fold
that do this.
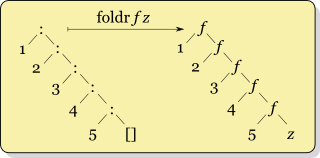
A linked list can be represented as a series of Link
constructors, where Link.rest is either another linked list or
the empty list.
We represent such a list in the diagram below:

In this diagram, the recursive list
Link(1, Link(2, Link(3, Link(4,Link(5)))))is represented with : as the constructor and [] as the empty list.
We define a function foldr that takes in a function f which takes two
arguments, and a value z. foldr essentially replaces the Link constructor
with f, and the empty list with z. It then evaluates the expression and
returns the result. This is equivalent to:
f(1, f(2, f(3, f(4, f(5, z)))))We call this operation a right fold.
Similarily we can define a left fold foldl that folds a list starting
from the beginning, such that the function f will be applied this
way:
f(f(f(f(f(z, 1), 2), 3), 4), 5)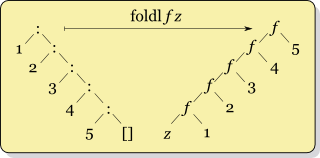
Also notice that a left fold is equivalent to Python's reduce with a starting
value.
Write the left fold function by filling in the blanks.
def foldl(link, fn, z):
""" Left fold
>>> lst = Link(3, Link(2, Link(1)))
>>> foldl(lst, sub, 0) # (((0 - 3) - 2) - 1)
-6
>>> foldl(lst, add, 0) # (((0 + 3) + 2) + 1)
6
>>> foldl(lst, mul, 1) # (((1 * 3) * 2) * 1)
6
"""
if link is Link.empty:
return z
"*** YOUR CODE HERE ***"
return foldl(______, ______, ______)
return foldl(link.rest, fn, fn(z, link.first))Now write the right fold function.
def foldr(link, fn, z):
""" Right fold
>>> lst = Link(3, Link(2, Link(1)))
>>> foldr(lst, sub, 0) # (3 - (2 - (1 - 0)))
2
>>> foldr(lst, add, 0) # (3 + (2 + (1 + 0)))
6
>>> foldr(lst, mul, 1) # (3 * (2 * (1 * 1)))
6
"""
"*** YOUR CODE HERE ***"
if link is Link.empty:
return z
return fn(link.first, foldr(link.rest, fn, z))Write foldl using foldr! You only need to fill in the step
function.
identity = lambda x: x
def foldl2(link, fn, z):
""" Write foldl using foldr
>>> list = Link(3, Link(2, Link(1)))
>>> foldl2(list, sub, 0) # (((0 - 3) - 2) - 1)
-6
>>> foldl2(list, add, 0) # (((0 + 3) + 2) + 1)
6
>>> foldl2(list, mul, 1) # (((1 * 3) * 2) * 1)
6
"""
def step(x, g):
"*** YOUR CODE HERE ***"
return lambda a: g(fn(a, x)) return foldr(link, step, identity)(z)