Homework 9
Due by 11:59pm on Monday, 5/9
Instructions
Download hw09.zip. Inside the archive, you will find a file called hw09.py, along with a copy of the OK autograder.
Submission: When you are done, submit with python3 ok
--submit. You may submit more than once before the deadline; only the
final submission will be scored. See Lab 0 for instructions on submitting
assignments.
Using OK: If you have any questions about using OK, please refer to this guide.
This homework set is completely optional. It consists of an assortment of exercises taken from the course topics. Do as much or as little as you want. You'll get EC for submitting at least Questions 1 and 2.
Remember to vote for your favorite Scheme art entries by Wednesday, May 4! You'll get EC for voting too.
Question 1: Nearest Power of Two
Implement the function nearest_two, which takes as input a positive number
x and returns the power of two (..., 1/8, 1/4, 1/2, 1, 2, 4, 8, ...) that is
nearest to x. If x is exactly between two powers of two, return the larger.
You may change the starter implementation if you wish.
def nearest_two(x):
"""Return the power of two that is nearest to x.
>>> nearest_two(8) # 2 * 2 * 2 is 8
8.0
>>> nearest_two(11.5) # 11.5 is closer to 8 than 16
8.0
>>> nearest_two(14) # 14 is closer to 16 than 8
16.0
>>> nearest_two(2015)
2048.0
>>> nearest_two(.1)
0.125
>>> nearest_two(0.75) # Tie between 1/2 and 1
1.0
>>> nearest_two(1.5) # Tie between 1 and 2
2.0
"""
power_of_two = 1.0
"*** YOUR CODE HERE ***"
return power_of_twoUse OK to test your code:
python3 ok -q nearest_twoQuestion 2: Smoothing
The idea of smoothing a function is a concept used in signal
processing among other things. If f is a one-argument function and dx is some small
number, then the smoothed version of f is the function whose value at
a point x is the average of f(x - dx), f(x), and f(x + dx).
Write a function smooth that takes as input a function f and a
value to use for dx and returns a function that computes the smoothed
version of f. Do not use any def statements inside of smooth; use
lambda expressions instead.
def smooth(f, dx):
"""Returns the smoothed version of f, g where
g(x) = (f(x - dx) + f(x) + f(x + dx)) / 3
>>> square = lambda x: x ** 2
>>> round(smooth(square, 1)(0), 3)
0.667
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q smoothIt is sometimes valuable to repeatedly smooth a function (that is,
smooth the smoothed function, and so on) to obtain the n-fold
smoothed function. Show how to generate the n-fold smoothed function,
n_fold_smooth, of any given function using your smooth function and
repeated function:
def repeated(f, n):
"""Returns a single-argument function that takes a value, x, and applies
the single-argument function F to x N times.
>>> repeated(lambda x: x*x, 3)(2)
256
"""
def h(x):
for k in range(n):
x = f(x)
return x
return hAs with smooth, use lambda expressions
rather than def statements in the body of n_fold_smooth.
def n_fold_smooth(f, dx, n):
"""Returns the n-fold smoothed version of f
>>> square = lambda x: x ** 2
>>> round(n_fold_smooth(square, 1, 3)(0), 3)
2.0
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q n_fold_smoothQuestion 3: Almost Golden
A near-golden rectangle has width w and height h where h/w is close to
w/h - 1. For example, in an 8 by 13 rectangle, the difference between 8/13 and
5/8 is less than 0.01. Implement near_golden, which returns the height of a
near-golden rectangle.
The near_golden function takes an even integer perimeter greater than
3 as its argument. It returns the integer height h of a rectangle with
the given perimeter that has the smallest possible difference between h/w
and w/h - 1.
Hints: The perimeter of a rectangle is w+w+h+h. Since h and perimeter
are integers, w must be an integer as well. The built-in abs function
returns the absolute value of a number.
def near_golden(perimeter):
"""Return the integer height of a near-golden rectangle with PERIMETER.
>>> near_golden(42) # 8 x 13 rectangle has perimeter 42
8
>>> near_golden(68) # 13 x 21 rectangle has perimeter 68
13
>>> result = near_golden(100) # return, don't print
>>> result
19
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q near_goldenQuestion 4: Graph Cycles
A graph in computer science refers to a structure such as this:
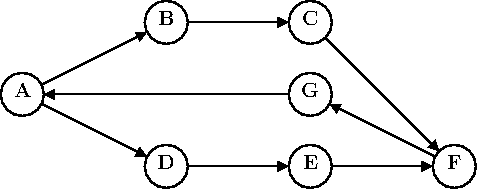
The circles are called vertices (singular vertex) and the lines joining vertices are called edges. The letters in the vertices are vertex labels.
This particular graph is directed, meaning that the edges have a
direction (shown by the arrows). We say that a directed graph is
cyclic if there is a path constructed from edges that leads from some
vertex back to itself. For example, the sample graph is cyclic
because, among other examples, one can follow edges from
A->B->C->F->G->A.
If we identify the vertices of a graph by their labels, then we can represent a graph as a dictionary mapping each vertex label L to a list successor vertices' labels (vertices at the other ends of arrows pointing out of L). Thus, the sample graph would be:
G = { 'A': ['B', 'D'], 'B': ['C'], 'C': ['F'], 'D': ['E'],
'E': ['F'], 'F': ['G'], 'G': ['A'] }Dag Hacker has developed the following program to determine if a graph represented in this fashion is circular:
def is_circular(G):
"""Return true iff G represents a circular directed graph."""
for v in G:
if reaches_circularity(G, v):
return True
return False
def reaches_circularity(G, v0):
"""Returns true if there is a circularity in G in some path
starting from vertex V0."""
def is_path_to_cycle(v1):
for w in G[v1]:
if v0 == w:
return True
if is_path_to_cycle(w):
return True
return False
return is_path_to_cycle(v0)Unfortunately, his reaches_circularity function does not always work.
It gives correct answers on acyclic graphs (graphs that are not
cyclic), but often goes into infinite loops on cyclic ones. Fill in
the program below to fix Dag's problem:
def reaches_circularity(G, v0):
"""Returns true if there is a circularity in G in some path
starting from vertex V0.
>>> G = { 'A': ['B', 'D'], 'B': ['C'], 'C': ['F'], 'D': ['E'],
... 'E': ['F'], 'F': ['G'], 'G': ['A'] }
>>> is_circular(G)
True
>>> G['F'] = []
>>> is_circular(G)
False
"""
"*** YOUR CODE HERE ***"
Hint: The problem has to do with what happens if there is a cycle in a path that starts at vertex v, but does not include v itself.
Use OK to test your code:
python3 ok -q reaches_circularityQuestion 5: Find Intersection
Implement intersection, which takes two linked lists, xs and ys, and finds
the Link at which the two linked list begin to intersect (or overlap).
You may assume that xs and ys are normal, non-circular linked lists, so that
they will always overlap at Link.empty (at least).
For the two linked lists below, z1 should be the start of the linked list that
you return. You are not simply looking to see if the Links in the overlapping
part have the same first fields; you are trying to find the first Link object
that is part of both lists.
See if you can find a way to do this in θ(n) time (where n is the
sum of the lengths of xs and
ys), and with constant additional space (i.e., without introducing any
Python lists, or creating new Links; just using a few integer or Link-valued
local variables.)
xs: x1 -> z1 -> z2 -> z3 -> ...
^
|
ys: y1 -> y2 -> y3Hint: How would you do this given two lists of the same length?
def intersection(xs, ys):
"""
>>> a = Link(1)
>>> intersection(a, Link.empty) is Link.empty
True
>>> b = a
>>> intersection(a, b).first # intersection begins at a
1
>>> looks_like_a = Link(1)
>>> intersection(a, looks_like_a) is Link.empty # no intersection! (identity vs value)
True
>>> b = Link(1, Link(2, Link(3, a)))
>>> a.first = 5
>>> intersection(a, b).first # intersection begins at a
5
>>> c = Link(3, b)
>>> intersection(b, c).first # intersection begins at b
1
>>> intersection(c, b).first # intersection begins at b
1
>>> intersection(a, c).first # intersection begins at a
5
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q intersectionQuestion 6: Deck of cards
Write a list comprehension that will create a deck of cards, given a
list of suits and a list of ranks. Each
element in the list will be a card, which is represented by a 2-element list
of the form [suit, rank].
def deck(suits, ranks):
"""Creates a deck of cards (a list of 2-element lists) with the given
suits and ranks. Each element in the returned list should be of the form
[suit, rank].
>>> deck(['S', 'C'], [1, 2, 3])
[['S', 1], ['S', 2], ['S', 3], ['C', 1], ['C', 2], ['C', 3]]
>>> deck(['S', 'C'], [3, 2, 1])
[['S', 3], ['S', 2], ['S', 1], ['C', 3], ['C', 2], ['C', 1]]
>>> deck([], [3, 2, 1])
[]
>>> deck(['S', 'C'], [])
[]
"""
"*** YOUR CODE HERE ***"
return ______
Use OK to test your code:
python3 ok -q deckQuestion 7: Riffle Shuffle
The familiar riffle shuffle of a deck of cards (or in our case, of a sequence of things) results in a new configuration of cards in which the original top card is followed by the original middle card, then by the original second card, then the card after the middle, and so forth. Assuming the deck (sequence) contains an even number of cards, write a list comprehension that produces the shuffled sequence.
Hint: To write this as a single comprehension, you may find the expression
k%2, which evaluates to 0 on even numbers and 1 on odd numbers, to be useful.
def riffle(deck):
"""Produces a single, perfect riffle shuffle of DECK, consisting of
DECK[0], DECK[M], DECK[1], DECK[M+1], ... where M is position of the
second half of the deck. Assume that len(DECK) is even.
>>> riffle([3, 4, 5, 6])
[3, 5, 4, 6]
>>> riffle(range(20))
[0, 10, 1, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 17, 8, 18, 9, 19]
"""
"*** YOUR CODE HERE ***"
return _______
Use OK to test your code:
python3 ok -q riffleQuestion 8: Advanced Counter
Complete the definition of make_advanced_counter_maker,
which creates a function that creates counters. These counters can not
only update their personal count, but also a shared count for all
counters. They can also reset either count.
def make_advanced_counter_maker():
"""Makes a function that makes counters that understands the
messages "count", "global-count", "reset", and "global-reset".
See the examples below:
>>> make_counter = make_advanced_counter_maker()
>>> tom_counter = make_counter()
>>> tom_counter('count')
1
>>> tom_counter('count')
2
>>> tom_counter('global-count')
1
>>> jon_counter = make_counter()
>>> jon_counter('global-count')
2
>>> jon_counter('count')
1
>>> jon_counter('reset')
>>> jon_counter('count')
1
>>> tom_counter('count')
3
>>> jon_counter('global-count')
3
>>> jon_counter('global-reset')
>>> tom_counter('global-count')
1
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q make_advanced_counter_makerQuestion 9: Balanced Tree
The sequence_to_tree function takes a linked list and converts it into
a balanced Tree in which every sub-tree has at most two branches. For every
subtree with 2 branches, all nodes in the left branch came before the label
of the root in the linked list and all nodes in the right branch came
after the label of the root.
A Tree is balanced if
- It is a leaf, or
- It has exactly one branch and that is a leaf, or
- It has two branches and the number of nodes in its first branch differs from the number of nodes in its second branch by at most 1, and both branches are also balanced.
In order to write sequence_to_tree, implement partial_tree(s, n),
which converts the first n elements of the sorted linked list s into a
balanced Tree. The return value is a two-element tuple: the resulting
balanced tree; and the rest of the linked list.
Hint: This function requires two recursive calls. The first call builds a left branch out of the first
left_sizeelements of s; Then, the next element is used as the entry of the returned tree. Finally, the second recursive call builds the right branch out of the nextright_sizeelements. In total,(left_size + 1 + right_size) = n, where 1 is for the entry:
def partial_tree(s, n):
"""Return a balanced tree of the first n elements of Link s, along with
the rest of s.
Examples of balanced trees:
Tree(1) # leaf
Tree(1, [Tree(2)]) # one branch is a leaf
Tree(1, [Tree(2), Tree(3)]) # two branches with one node each
Examples of unbalanced trees:
Tree(1, [Tree(2, [Tree(3)])]) # one branch not a leaf
Tree(1, [Tree(2), # Mismatch: branch with 1 node
Tree(3, [Tree(4, [Tree(5)])])]) # vs branch with 3 nodes
>>> s = Link(1, Link(2, Link(3, Link(4, Link(5)))))
>>> partial_tree(s, 3)
(Tree(2, [Tree(1), Tree(3)]), Link(4, Link(5)))
>>> t = Link(-2, Link(-1, Link(0, s)))
>>> partial_tree(t, 7)[0]
Tree(1, [Tree(-1, [Tree(-2), Tree(0)]), Tree(3, [Tree(2), Tree(4)])])
>>> partial_tree(t, 7)[1]
Link(5)
"""
if n == 1:
return (Tree(s.first), s.rest)
elif n == 2:
return (Tree(s.first, [Tree(s.rest.first)]), s.rest.rest)
else:
left_size = (n-1)//2
right_size = n - left_size - 1
"*** YOUR CODE HERE ***"
def sequence_to_tree(s):
"""Return a balanced tree containing the elements of sorted Link s.
Note: this implementation is complete, but the definition of partial_tree
above is not complete.
>>> sequence_to_tree(Link(1, Link(2, Link(3))))
Tree(2, [Tree(1), Tree(3)])
>>> elements = Link(1, Link(2, Link(3, Link(4, Link(5, Link(6, Link(7)))))))
>>> sequence_to_tree(elements)
Tree(4, [Tree(2, [Tree(1), Tree(3)]), Tree(6, [Tree(5), Tree(7)])])
"""
return partial_tree(s, len(s))[0]Use OK to test your code:
python3 ok -q partial_tree
python3 ok -q sequence_to_tree