Homework 5
Due by 11:59pm on Monday, 3/13
Instructions
Download hw05.zip.
Submission: When you are done, submit with
python3 ok --submit.
You may submit more than once before the deadline; only the final submission
will be scored. Check that you have successfully submitted your code on
okpy.org.
See Lab 0
for more instructions on submitting assignments.
Using OK: If you have any questions about using OK, please refer to this guide.
Readings: You might find the following references useful:
Vitamins
Question 1: Countdown
Write both a generator function and an iterator (that is not a generator) that count down to 0.
def countdown(n):
"""
A generator that counts down from N to 0.
>>> for number in countdown(5):
... print(number)
...
5
4
3
2
1
0
>>> for number in countdown(2):
... print(number)
...
2
1
0
"""
"*** YOUR CODE HERE ***"
class Countdown:
"""
An iterator that counts down from N to 0.
>>> for number in Countdown(5):
... print(number)
...
5
4
3
2
1
0
>>> for number in Countdown(2):
... print(number)
...
2
1
0
"""
def __init__(self, cur):
self.cur = cur
def __next__(self):
"*** YOUR CODE HERE ***"
def __iter__(self):
"""So that we can use this iterator as an iterable."""
return selfUse OK to test your code:
python3 ok -q countdown
python3 ok -q CountdownRequired Questions
Simplifying Expressions
Question 2
In lecture, you saw that one use of trees is in representing expressions
(such as arithmetic expressions). So, for example, the expression
2 * (3 + x) can be represented as the tree
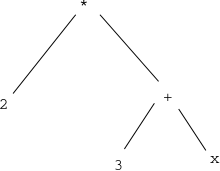
That is, each operand is a child of the operator that applies to it.
In lecture, we looked at evaluating an expression that contains only numbers
and operators. For this problem, we'll work at simplifying an expression
that may contain variables without necessarily evaluating it. For example,
2 * (x + 0) + y * 0 could be simplified to 2 * x.
For this problem, the only operators are *, +, and - (as strings), and
the labels of leaves
will either be numbers or strings containing variable names. Thus, our first
example would be represented with
Tree('*', [Tree(2), Tree('+', [Tree(3), Tree('x')])])To help you, we've defined a few useful things that may come in handy:
# Alternative names of parts of an expression tree.
class Expr(Tree):
num_exprs = 0
def __init__(self, op, *branches):
"""For convenience, an Expr may be constructed as Expr(op, [c1, ...])
or Expr(op, c1, ...)."""
Expr.num_exprs += 1
if len(branches) == 1 and type(branches[0]) is list:
super().__init__(op, branches[0])
else:
super().__init__(op, list(branches))
# The following methods allow you to write E.oper, E[k] for the label
# and kth child of E, in keeping with the usual language for dealing with
# expressions. The class inherits from Tree, to == is also defined.
@property
def oper(self):
return self.label
def __getitem__(self, k):
return self.branches[k]
def __setitem__(self, k, v):
self.branches[k] = v
def arity(self):
"""The number of operands in this expression."""
return len(self.branches)
# Useful constants:
ZERO = Expr(0)
ONE = Expr(1)
def postfix_to_expr(postfix_expr):
"""Return an expression tree equivalent to POSTFIX_EXPR, a string
in postfix ("reverse Polish") notation. In postfix, one writes
E1 OP E2 (where E1 and E2 are expressions and OP is an operator) as
E1' E2' OP, where E1' and E2' are the postfix versions of E1 and E2. For
example, '2*(3+x)' is written '2 3 x + *' and '2*3+x' is `2 3 * x +'.
>>> print_tree(postfix_to_expr("2 3 x + *"))
*
2
+
3
x
"""
def expr_to_infix(expr):
"""A string containing a standard infix denotation of the expression
tree EXPR"""Implement the function simplify on these trees. Given an expression tree
expr, this function returns a new expression tree, simplified from expr by
applying the following rules:
- the expressions
E * 0and0 * E, whereEhere can be any expression tree, are replaced by0. - the expressions
E * 1and1 * Eare replaced byE. - the expressions
E + 0,0 + E, andE - 0are replaced byE. - the expression
E - E(where the two operands are identical trees) is replaced by0.
These simplifications may cause a cascade, as in y * (x - (0 + x)) which
simplifies to y * (x - x), then to y * 0, and then to 0. In order for
that to work, you must be careful to simplify operands before simplifying the
whole expression. Your solution must be nondestructive.
def simplify(expr):
"""EXPR must be an expression tree involving the operators
'+', '*', and '-' in inner nodes; numbers and strings (standing for
variable names) in leaves. Returns an equivalent, simplified version
of EXPR.
>>> def simp(postfix_expr):
... v0 = postfix_to_expr(postfix_expr)
... v1 = postfix_to_expr(postfix_expr)
... r = expr_to_infix(simplify(v0))
... assert v0 == v1, "Input was modified by simplify"
... return r
>>> simp("x y + 0 *")
'0'
>>> simp("0 x y + *")
'0'
>>> simp("x y + 0 +")
'(x + y)'
>>> simp("0 x y + +")
'(x + y)'
>>> simp("x y + 1 *")
'(x + y)'
>>> simp("1 x y + *")
'(x + y)'
>>> simp("x y + x y + -")
'0'
>>> simp("x y y - + x - a b * *")
'0'
>>> simp("x y 3 * -")
'(x - (y * 3))'
>>> simp("x y 0 + 3 * -")
'(x - (y * 3))'
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q simplifyQuestion 3
Implement the method dsimplify, which is supposed to produce the same result as
simplify, but destructively and without creating any new tree nodes.
def dsimplify(expr):
"""EXPR must be an expression tree involving the operators
'+', '*', and '-' in inner nodes; numbers and strings (standing for
variable names) in leaves. Returns an equivalent, simplified version
of EXPR.
>>> def simp(postfix_expr):
... expr = postfix_to_expr(postfix_expr)
... cnt0 = Expr.num_exprs
... v = expr_to_infix(dsimplify(expr))
... assert cnt0 == Expr.num_exprs, "New expression trees created."
... return v
>>> simp("x y + 0 *")
'0'
>>> simp("0 x y + *")
'0'
>>> simp("x y + 0 +")
'(x + y)'
>>> simp("0 x y + +")
'(x + y)'
>>> simp("x y + 1 *")
'(x + y)'
>>> simp("1 x y + *")
'(x + y)'
>>> simp("x y + x y + -")
'0'
>>> simp("x y y - + x - a b * *")
'0'
>>> simp("x y 3 * -")
'(x - (y * 3))'
>>> simp("x y 0 + 3 * -")
'(x - (y * 3))'
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q dsimplifyQuestion 4: Vending Machine
Create a class called VendingMachine that represents a vending
machine for some product. A VendingMachine object returns strings
describing its interactions. See the doctest below for examples:
class VendingMachine:
"""A vending machine that vends some product for some price.
>>> v = VendingMachine('candy', 10)
>>> v.vend()
'Machine is out of stock.'
>>> v.restock(2)
'Current candy stock: 2'
>>> v.vend()
'You must deposit $10 more.'
>>> v.deposit(7)
'Current balance: $7'
>>> v.vend()
'You must deposit $3 more.'
>>> v.deposit(5)
'Current balance: $12'
>>> v.vend()
'Here is your candy and $2 change.'
>>> v.deposit(10)
'Current balance: $10'
>>> v.vend()
'Here is your candy.'
>>> v.deposit(15)
'Machine is out of stock. Here is your $15.'
>>> w = VendingMachine('soda', 2)
>>> w.restock(3)
'Current soda stock: 3'
>>> w.deposit(2)
'Current balance: $2'
>>> w.vend()
'Here is your soda.'
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q VendingMachineQuestion 5: Merge
Implement merge(s0, s1), which takes two iterables s0 and s1 whose
elements are ordered. merge yields elements from s0 and s1 in sorted
order, eliminating repetition. You may assume s0 and s1 themselves do not
contain repeats, and that none of the elements of either are None.
You may not assume that the iterables are finite; either may produce an infinite
stream of results.
You will probably find it helpful to use the two-argument version of the built-in
next function: next(s, v) is the same as next(s), except that instead of
raising StopIteration when s runs out of elements, it returns v.
See the doctest for examples of behavior.
def merge(s0, s1):
"""Yield the elements of strictly increasing iterables s0 and s1, removing
repeats. Assume that s0 and s1 have no repeats. You can also assume that s0
and s1 represent infinite sequences.
>>> m = merge([0, 2, 4, 6, 8, 10, 12, 14], [0, 3, 6, 9, 12, 15])
>>> type(m)
<class 'generator'>
>>> list(m)
[0, 2, 3, 4, 6, 8, 9, 10, 12, 14, 15]
>>> def big(n):
... k = 0
... while True: yield k; k += n
>>> m = merge(big(2), big(3))
>>> [next(m) for _ in range(11)]
[0, 2, 3, 4, 6, 8, 9, 10, 12, 14, 15]
"""
i0, i1 = iter(s0), iter(s1)
e0, e1 = next(i0, None), next(i1, None)
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q mergeExtra Questions
Extra questions are not worth extra credit and are entirely optional. They are designed to challenge you to think creatively!
Question 6: Zip generator
For this problem, we will be writing zip_generator, which yields a
series of lists, each containing the nth items of each iterable.
It should stop when the smallest iterable runs out of elements.
def zip(*iterables):
"""
Takes in any number of iterables and zips them together.
Returns a generator that outputs a series of lists, each
containing the nth items of each iterable.
>>> z = zip([1, 2, 3], [4, 5, 6], [7, 8])
>>> for i in z:
... print(i)
...
[1, 4, 7]
[2, 5, 8]
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q zip