Dictionaries, Matrices, and Trees
Today will cover...
- Announcements
- Dictionary type
- Matrix abstraction
- Tree abstraction
- Tree processing
Review: Layers of abstraction
| Primitive Representation | 1 2 3 True False(..,..) [..,..] |
Data abstraction | make_rat() numer() denom() |
add_rat() mul_rat() print_rat() equal_rat() |
|
| User program | exact_harmonic_number() |
Each layer only uses the layer above it.
Review: Python types
| Type | Examples |
|---|---|
| Integers | 0 -1 0xFF 0b1101 |
| Booleans | True False |
| Functions | def f(x)...
lambda x: ...
|
| Strings | "pear""I say, \"hello!\"" |
| Tuples | (1, 10) ("Oh", "hi", 11) |
| Ranges | range(11) range(1, 6) |
| Lists | [] ["apples", "bananas"][x**3 for x in range(2)]
|
Dictionaries
A dict is a mutable mapping of key-value pairs
states = {
"CA": "California",
"DE": "Delaware",
"NY": "New York",
"TX": "Texas",
"WY": "Wyoming"
}
Queries:
>>> len(states)
5
>>> "CA" in states
True
>>> "ZZ" in states
False
Dictionary selection
words = {
"más": "more",
"otro": "other",
"agua": "water"
}
Select a value:
>>> words["otro"]
'other'
>>> first_word = "agua"
>>> words[first_word]
'water'
>>> words["pavo"]
KeyError: pavo
>>> words.get("pavo", "🤔")
'🤔'
Dictionary mutation
Create an empty dict:
users = {}
Add values:
users["profpamela"] = "b3stp@ssEvErDontHackMe"
Change values:
users["profpamela"] += "itsLongerSoItsMoreSecure!!"
>>> users["profpamela"]
'b3stp@ssEvErDontHackMeitsLongerSoItsMoreSecure!!'
Dictionary rules
- A key cannot be a list or dictionary (or any mutable type)
- All keys in a dictionary are distinct (there can only be one value per key)
- The values can be any type, however!
spiders = {
"smeringopus": {
"name": "Pale Daddy Long-leg",
"length": 7
},
"holocnemus pluchei": {
"name": "Marbled cellar spider",
"length": (5, 7)
}
}
Dictionary iteration
insects = {"spiders": 8, "centipedes": 100, "bees": 6}
for name in insects:
print(insects[name])
...is the same as:
for name in list(insects):
print(insects[name])
What will be the order of items?
8 100 6
Keys are iterated over in the order they are first added.
Nested data
| Lists of lists | [ [1, 2], [3, 4] ] |
| Lists of tuples | [ (1, 2), (3, 4) ] |
| Tuples of tuples | ( (1, 2), (3, 4) ) |
| Dicts of tuples | {"x": (1, 2), "y": (3, 4)} |
| Dicts of lists | {"heights": [89, 97], "ages": [6, 8]} |
...what else?! Dicts of dicts, Lists of dicts, etc.
Next up: more abstractions
Matrices
Consider a matrix (two-dimensional table) like this:
| 1 | 2 | 0 | 4 |
| 0 | 1 | 3 | -1 |
| 0 | 0 | 1 | 8 |
That matrix has three rows and four columns, with integer values in each location.
Matrices: Data abstraction
We want this constructor, selector, and mutator:
matrix(rows, cols) |
Returns a ROWS x COLS matrix with all values set to 0 |
value(matrix, row, col) |
Returns value of MATRIX at (ROW, COL) |
set_value(matrix, row, col, val) |
Sets value of MATRIX at (ROW, COL) to VAL |
How could we implement? Answer the poll!
Matrices: Implementation A
A list of lists, row-major order:
[ [1,2,0,4], [0,1,3,-1], [0,0,1,8] ]
def matrix(rows, cols):
return [ [0 for col in range(cols)] for row in range(rows) ]
def value(matrix, row, col):
return matrix[row][col]
def set_value(matrix, row, col, val):
matrix[row][col] = val
m = matrix(3, 4)
set_value(m, 0, 0, 1)
set_value(m, 0, 1, 2)
set_value(m, 0, 3, 4)
Matrices: Implementation B
A list of lists, column-major order:
[ [1,0,0], [2,1,0], [0,3,1], [4,-1,8] ]
def matrix(rows, cols):
return [ [0 for row in range(rows)] for col in range(cols) ]
def value(matrix, row, col):
return matrix[col][row]
def set_value(matrix, row, col, val):
matrix[col][row] = val
m = matrix(3, 4)
set_value(m, 0, 0, 1)
set_value(m, 0, 1, 2)
set_value(m, 0, 3, 4)
Matrices: Implementation C
A tuple of lists, row-major order:
( [1,0,0], [2,1,0], [0,3,1], [4, -1,8] )
def matrix(rows, cols):
return tuple( [0 for col in range(cols)] for row in range(rows) )
def value(matrix, row, col):
return matrix[row][col]
def set_value(matrix, row, col, val):
matrix[row][col] = val
m = matrix(3, 4)
set_value(m, 0, 0, 1)
set_value(m, 0, 1, 2)
set_value(m, 0, 3, 4)
Matrices: Implementation D ❌
A list of tuples?
[ (1,2,0,4), (0,1,3,-1), (0,0,1,8) ]
def matrix(rows, cols):
return [ tuple(0 for col in range(cols))
for row in range(rows) ]
def value(matrix, row, col):
return matrix[row][col]
def set_value(matrix, row, col, val):
matrix[row][col] = val
m = matrix(3, 4)
set_value(m, 0, 0, 1) ❌
set_value(m, 0, 1, 2) ❌
set_value(m, 0, 3, 4) ❌
Matrices: Implementation D2
A list of tuples?
[ (1,2,0,4), (0,1,3,-1), (0,0,1,8) ]
def matrix(rows, cols):
return [ tuple(0 for col in range(cols))
for row in range(rows) ]
def value(matrix, row, col):
return matrix[row][col]
def set_value(matrix, row, col, val):
matrix[row] = matrix[row][:col] + (val,) + matrix[row][col+1:]
m = matrix(3, 4)
set_value(m, 0, 0, 1)
set_value(m, 0, 1, 2)
set_value(m, 0, 3, 4)
Designing an implementation
Which implementation was your favorite?
Answer the poll!
When might you use a tuple?
When might you use a list?
When might you use a dict?
Trees

- Each oval is a node
- Top node is the root
- Each node is itself the root of another tree (called a subtree); the nodes immediately below are its children
- Nodes without children are leaves; others are inner nodes
- Each node generally has a label
Trees: Data abstraction
We want this constructor and selectors:
tree(label, children) |
Returns a tree with given LABEL at its root, whose children are CHILDREN |
label(tree) |
Returns the label of root node of TREE |
children(tree) |
Returns the children of TREE (each a tree). |
is_leaf(tree) |
Returns true if TREE is a leaf node. |
How could we implement? Answer the poll!
Trees: Implementation A
A list of label + list for each tree/subtree:
[20,[12,[9,[7],[2]],[3]],[8,[4],[4]]]
def tree(label, children=[]):
return [label] + children
def label(tree):
return tree[0]
def children(tree):
return tree[1:]
def is_leaf(tree):
return len(children(tree)) == 0
t = tree(20, [tree(12,
[tree(9,
[tree(7), tree(2)]),
tree(3)]),
tree(8,
[tree(4), tree(4)])])
Trees: Implementation B
A number-list tuple for each tree/subtree:
(20,[(12,[(9,[(7,[]),(2, [])]),(3, [])]),(8,[(4,[]),(4,[])])])
def tree(label, children=[]):
return (label, children)
def label(tree):
return tree[0]
def children(tree):
return tree[1]
t = tree(20, [tree(12,
[tree(9,
[tree(7), tree(2)]),
tree(3)]),
tree(8,
[tree(4), tree(4)])])
Trees: Implementation C
A dictionary for each tree/subtree:
{'l':20,'c':[{'l':12,'c':[{'l':9,'c':[{'l':7,'c': []},{'l':2,'c':[]}]},{'l':3,'c':[]}]},{'l':8,'c':[{'l':4,'c':[]},{'l':4,'c':[]}]}]}
def tree(label, children=[]):
return {"l": label, "c": children}
def label(tree):
return tree["l"]
def children(tree):
return tree["c"]
t = tree(20, [tree(12,
[tree(9,
[tree(7), tree(2)]),
tree(3)]),
tree(8,
[tree(4), tree(4)])])
Tree processing
A tree is a recursive structure.
Each tree has:
- A label
- 0 or more children, each a tree
Recursive structure implies recursive algorithm!
Tree processing: Counting leaves

def count_leaves(t):
"""Returns the number of leaf nodes in T."""
if is_leaf(t):
return 1
else:
children_leaves = 0
for c in children(t):
children_leaves += count_leaves(c)
return children_leaves
What's the base case? What's the recursive call?
Tree processing: Counting leaves
The sum()
function sums up the items of an iterable.
>>> sum([1, 1, 1, 1])
4
That leads to this shorter function:
def count_leaves(t):
"""Returns the number of leaf nodes in T."""
if is_leaf(t):
return 1
else:
return sum([count_leaves(c) for c in children(t)])
Creating trees
A function that creates a tree from another tree is also often recursive.

Creating trees: Doubling labels

def double(t):
"""Returns a tree identical to T, but with all labels doubled."""
if is_leaf(t):
return tree(label(t) * 2)
else:
return tree(label(t) * 2,
[double(c) for c in children(t)])
What's the base case? What's the recursive call?
Creating trees: Doubling labels
Longer...
def double(t):
"""Returns a tree identical to T, but with all labels doubled."""
if is_leaf(t):
return tree(label(t) * 2)
else:
doubled_children = []
for c in children(t):
doubled_children.append(double(c))
return tree(label(t) * 2, doubled_children)
Shorter!
def double(t):
"""Returns the number of leaf nodes in T."""
return tree(label(t) * 2,
[double(c) for c in children(t)])
Challenge: List of leaves
Try this on your own:
def list_of_leaves(t):
"""Return a list containing the leaf labels of T.
>>> leaves(t) # Using the t from the slides
[7, 2, 3, 4, 4]
"""
if ______:
return ______
else:
______
return ______
Hint: If you sum a list of lists, you get a list containing the elements of those lists. The sum function takes a second argument, the starting value of the sum.
Tree: Layers of abstraction
| Primitive Representation | 1 2 3 True False(..,..) [..,..] {...} |
| Data abstraction | tree() children() label() |
is_leaf() |
|
| User program | double(t) count_leaves(t) |
Each layer only uses the layer above it.
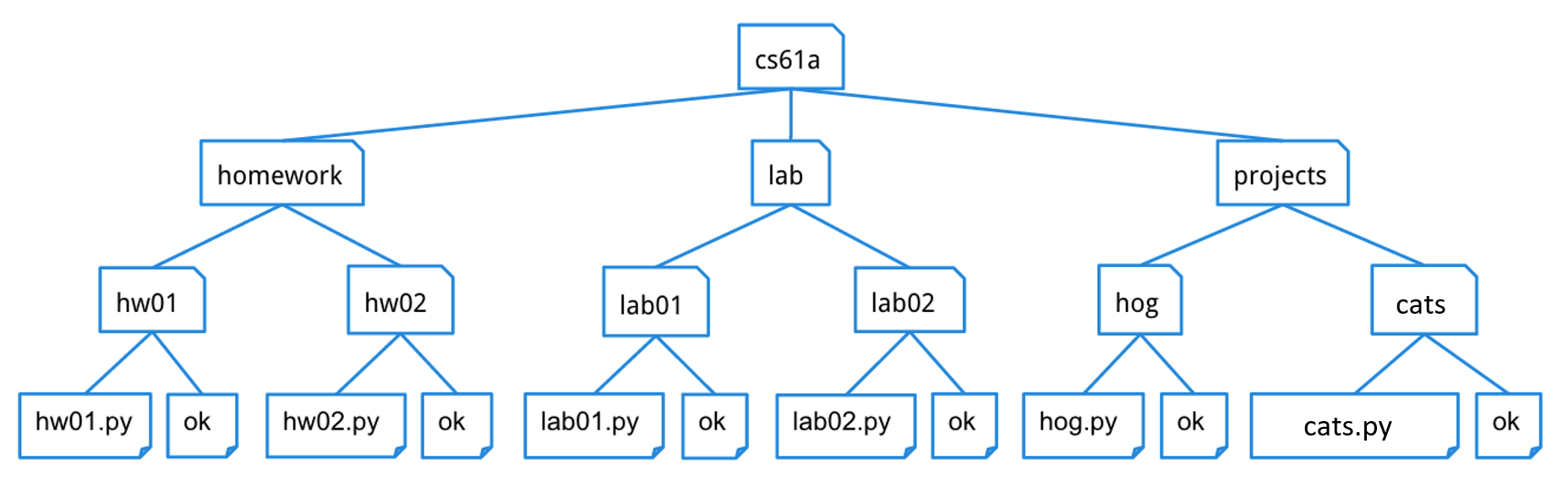
Trees, trees, everywhere!
Directory structures
Parse trees
For natural languages...

Key: S = Sentence, NP = Noun phrase, D = Determiner, N = Noun, V = Verb, VP = Verb Phrase
Parse trees
For programming languages, too...

Key: E = expression