Discussion 6: String Representation, Trees

disc06.pdf

This is an online worksheet that you can work on during discussions. Your work is not graded and you do not need to submit anything.

Representation: Repr, Str

There are two main ways to produce the "string" of an object in Python: str() and repr(). While the two are similar, they are used for different purposes.

str() is used to describe the object to the end user in a "Human-readable" form, while repr() can be thought of as a "Computer-readable" form mainly used for debugging and development.

When we define a class in Python, __str__ and __repr__ are both built-in methods for the class.

We can call those methods using the global built-in functions str(obj) or repr(obj) instead of dot notation, obj.__repr__() or obj.__str__().

In addition, the print() function calls the __str__ method of the object, while simply calling the object in interactive mode calls the _repr__ method.

Here's an example:

class Rational:

    def __init__(self, numerator, denominator):
        self.numerator = numerator
        self.denominator = denominator

    def __str__(self):
        return f'{self.numerator}/{self.denominator}'

    def __repr__(self):
        return f'Rational({self.numerator},{self.denominator})'

>>> a = Rational(1, 2)
>>> str(a)
'1/2'
>>> repr(a)
'Rational(1,2)'
>>> print(a)
1/2
>>> a
Rational(1,2)

Q1: WWPD: Repr-esentation

Note: This is not the typical way repr is used, nor is this way of writing repr recommended, this problem is mainly just to make sure you understand how repr and str work.

class A:
    def __init__(self, x):
        self.x = x

    def __repr__(self):
         return self.x

    def __str__(self):
         return self.x * 2

class B:
    def __init__(self):
         print('boo!')
         self.a = []

    def add_a(self, a):
         self.a.append(a)

    def __repr__(self):
         print(len(self.a))
         ret = ''
         for a in self.a:
             ret += str(a)
         return ret

Given the above class definitions, what will the following lines output?

>>> A('one')

>>> print(A('one'))

>>> repr(A('two'))

>>> b = B()

>>> b.add_a(A('a'))
>>> b.add_a(A('b'))
>>> b

Trees

In computer science, trees are recursive data structures that are widely used in various settings and can be implemented in many ways. The diagram below is an example of a tree.

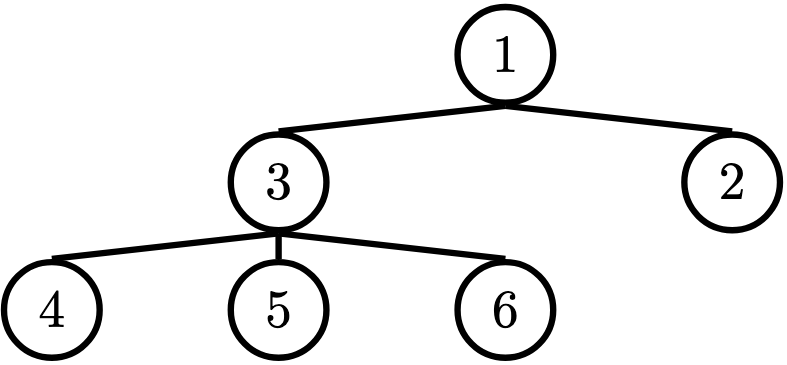
Example Tree

Generally in computer science, you may see trees drawn "upside-down" like so. We say the root is the node where the tree begins to branch out at the top, and the leaves are the nodes where the tree ends at the bottom.

Some terminology regarding trees:

Parent Node: A node that has at least one branch.
Child Node: A node that has a parent. A child node can only have one parent.
Root: The top node of the tree. In our example, this is the 1 node.
Label: The value at a node. In our example, every node's label is an integer.
Leaf: A node that has no branches. In our example, the 4, 5, 6, 2 nodes are leaves.
Branch: A subtree of the root. Trees have branches, which are trees themselves: this is why trees are recursive data structures.
Depth: How far away a node is from the root. We define this as the number of edges between the root to the node. As there are no edges between the root and itself, the root has depth 0. In our example, the 3 node has depth 1 and the 4 node has depth 2.
Height: The depth of the lowest (furthest from the root) leaf. In our example, the 4, 5, and 6 nodes are all the lowest leaves with depth 2. Thus, the entire tree has height 2.

In computer science, there are many different types of trees, used for different purposes. Some vary in the number of branches each node has; others vary in the structure of the tree.

A tree has a root value and a list of branches, where each branch is itself a tree.

The Tree constructor takes in a value label for the root, and an optional list of branches branches. If branches isn't given, the constructor uses the empty list [] as the default.
To get the label of a tree t, we access the instance attributes t.label.
Accessing the instance attribute t.branches will give us a list of branches. Treating the return value of t.branches as a list is then part of how we define trees.

With this in mind, we can create the tree from earlier using our constructor:

t = Tree(1,
      [Tree(3,
          [Tree(4),
           Tree(5),
           Tree(6)]),
      Tree(2)])

Q2: Height

Write a function that returns the height of a tree. Recall that the height of a tree is the length of the longest path from the root to a leaf.

Q3: Maximum Path Sum

Write a function that takes in a tree and returns the maximum sum of the values along any path in the tree. Recall that a path is from the tree's root to any leaf.

Q4: Find Path

Write a function that takes in a tree and a value x and returns a list containing the nodes along the path required to get from the root of the tree to a node containing x.

If x is not present in the tree, return None. Assume that the entries of the tree are unique.

For the following tree, find_path(t, 5) should return [2, 7, 6, 5]

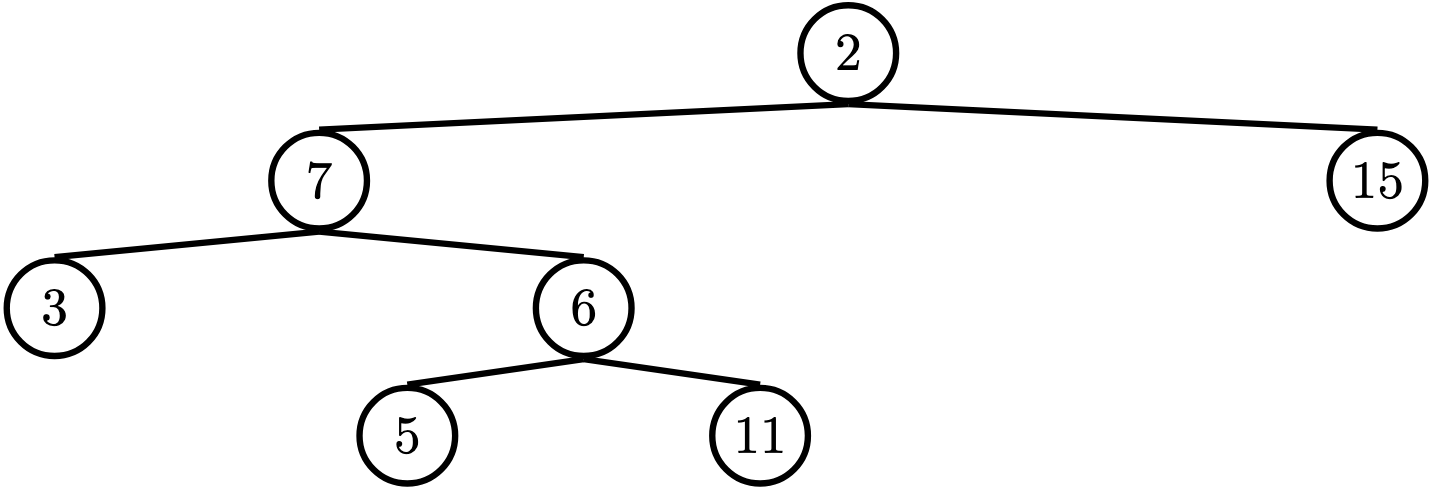
Example Tree

Q5: Prune Small

Complete the function prune_small that takes in a Tree t and a number n and prunes t mutatively. If t or any of its branches has more than n branches, the n branches with the smallest labels should be kept and any other branches should be pruned, or removed, from the tree.