Discussion 14: Final Review
Final Review
The following worksheet is final review! It covers various topics that have been seen throughout the semester.
Your TA will not be able to get to all of the problems on this worksheet so feel free to work through the remaining problems on your own. Bring any questions you have to office hours or post them on piazza.
Good luck on the final and congratulations on making it to the last discussion of CS61A!
Recursion
Q1: Paths List
(Adapted from Fall 2013) Fill in the blanks in the implementation of paths, which
takes as input two positive integers x and y. It returns a list of paths, where
each path is a list containing steps to reach y from x by repeated incrementing or
doubling. For instance, we can reach 9 from 3 by incrementing to 4, doubling to 8,
then incrementing again to 9, so one path is [3, 4, 8, 9]
Mutation
Q2: Reverse
Write a function that reverses the given list. Be sure to mutate the original list.
This is practice, so don't use the built-in reverse function!
Trees
Q3: Reverse Other
Write a function reverse_other that mutates the tree such that labels on
every other (odd-depth) level are reversed. For example,
Tree(1,[Tree(2, [Tree(4)]), Tree(3)]) becomes Tree(1,[Tree(3, [Tree(4)]), Tree(2)]).
Notice that the nodes themselves are not reversed; only the labels are.
Linked Lists
Q4: Multiply Links
Write a function that takes in a Python list of linked lists and multiplies them element-wise. It should return a new linked list.
If not all of the Link objects are of equal length, return a
linked list whose length is that of the shortest linked list given. You
may assume the Link objects are shallow linked lists, and that
lst_of_lnks contains at least one linked list.
Scheme
Q5: Group by Non-Decreasing
Define a function nondecreaselist, which takes in a scheme list of numbers and outputs a list of lists, which overall has the same numbers in the same order, but grouped into lists that are non-decreasing.
For example, if the input is a stream containing elements
(1 2 3 4 1 2 3 4 1 1 1 2 1 1 0 4 3 2 1)the output should contain elements
((1 2 3 4) (1 2 3 4) (1 1 1 2) (1 1) (0 4) (3) (2) (1))Note: The skeleton code is just a suggestion; feel free to use your own structure if you prefer.
Run in 61A CodeEnvironment Diagrams
Q6: To Scheme An Environment Diagram
mu, implemented in the Scheme project as MuProcedure, allows us to create
procedures that are dynamically scoped.
This means that calling a mu procedure creates a new frame whose parent is
the frame in which it was called (dynamic scoping).
In contrast, calling a lambda procedure creates a new frame whose parent is
the frame in which it was defined (lexical scoping).
You can also find mu described in the
Scheme Specification.
For an interactive version of each diagram, copy-paste the code into 61A Code, and click the yellow bug icon on the top right. That icon starts up the debugger and environment diagram visualizer for code.cs61a.org.
Say that we are given the following section of code:
(define lamb2 (lambda (x) (+ x y)))
(define cow2 (mu (x) (+ x y)))
(define y 5)
(lamb2 1)
(cow2 1)Running the full code results in this environment diagram:
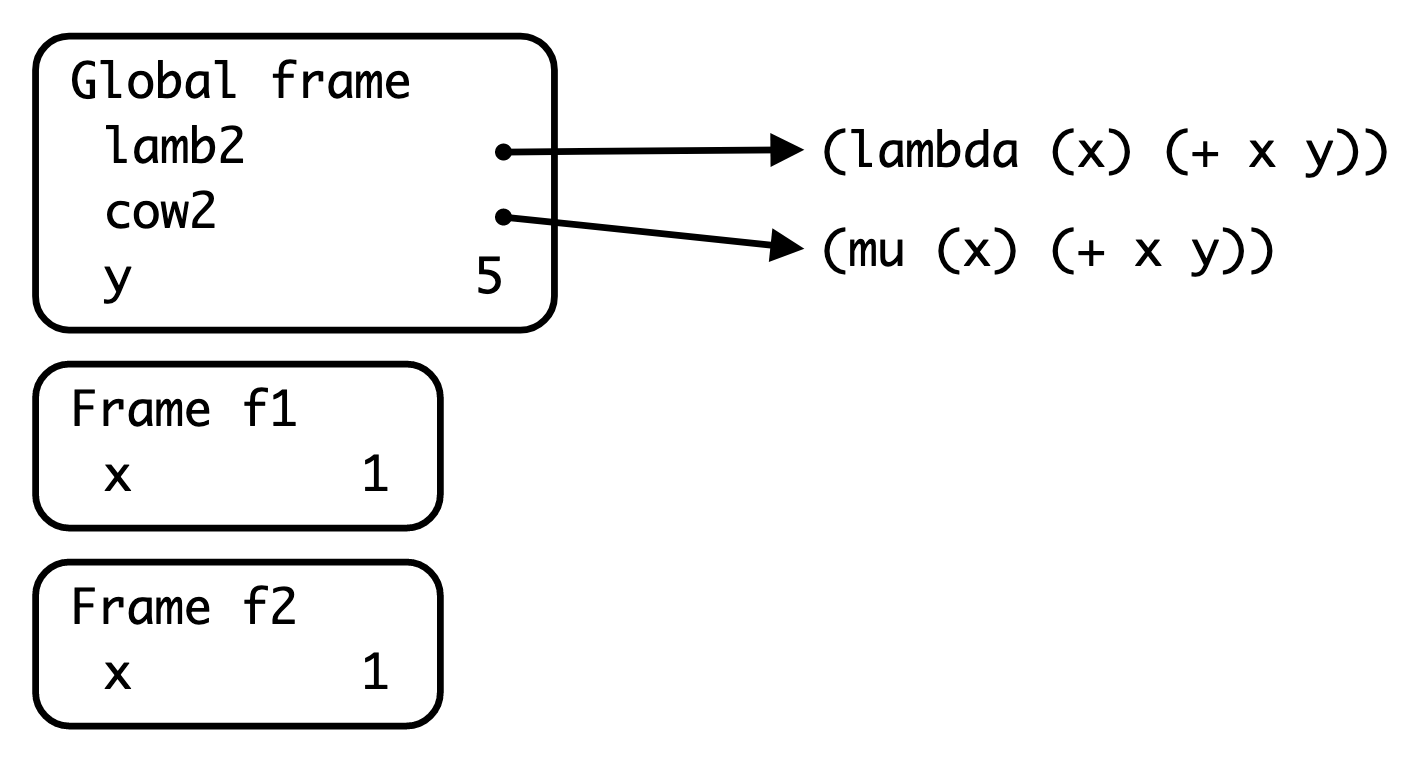
What is the parent frame of frame f1?
What is the parent frame of frame f2?
Now let's say we have the following section of code:
(define (goat x y) (lambda (x) (+ x y)))
(define (horse x y) (mu (x) (+ x y)))
(define horns (goat 1 2))
(define saddle (horse 1 2))
(define x 10)
(define y 20)
(horns 5)
(saddle 5)Running the entire code block gives you the diagram:
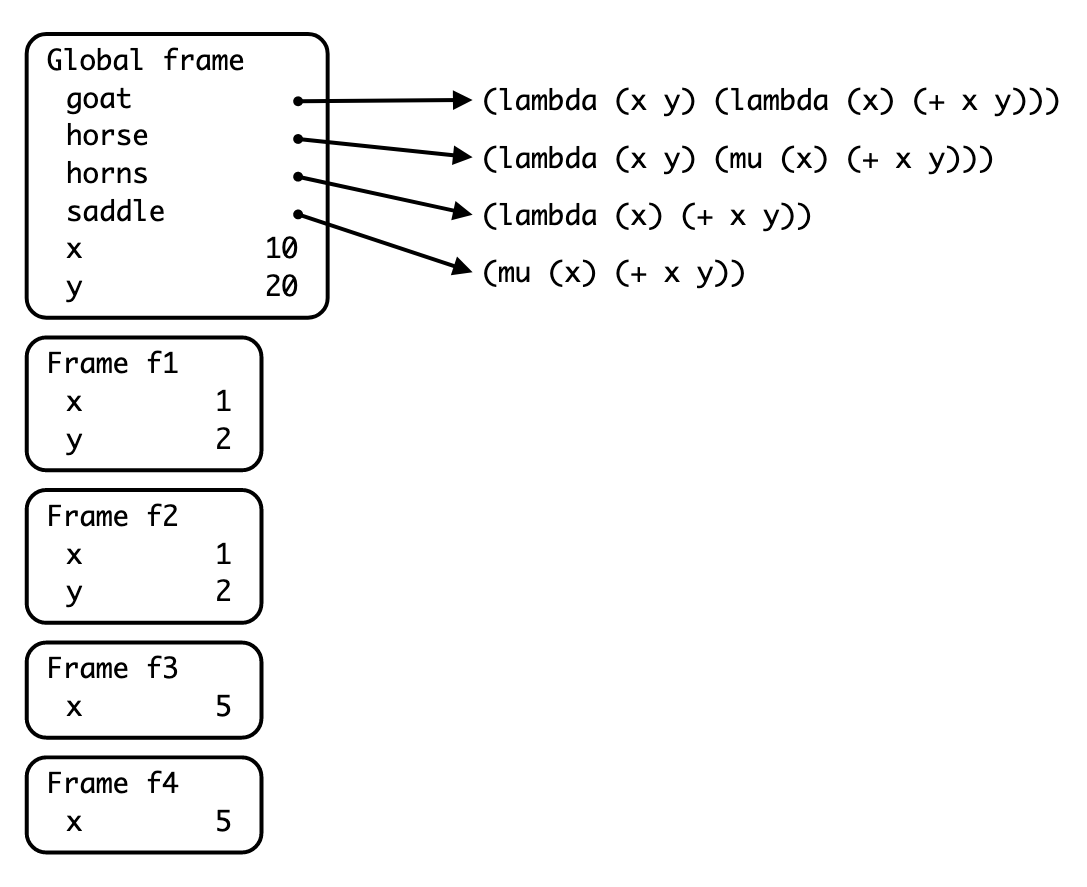
Which frame is created by the call to (goat 1 2), and what is the parent of
this frame?
What kind of procedure is horns, and what scoping rule does it use?
Which frame is created by the call to (horse 1 2), and what is the parent of
this frame?
What kind of procedure is saddle, and what scoping rule does it use?
Which frame is created by the call to (horns 5), and what is the parent of
this frame?
Which frame is created by the call to (saddle 5), and what is the parent of
this frame?
What would be the output of the lines (horns 5) and (saddle 5)?
Would there be any difference in output if horse was defined using a lambda
as opposed to a define, e.g. (define horse (lambda (x y) ...)? If so, what?
Programs as Data
Q7: Or with Multiple Args
Implement make-long-or, which returns, as a list, a program that takes in any number of expressions and or's them together (applying short-circuiting rules). This procedure should do this without using the or special form. Unlike the make-or procedure, the arguments will be passed in as a list named args.
The behavior of the or procedure is specified by the following doctests:
scm> (define or-program (make-long-or '((print 'hello) (/ 1 0) 3 #f)))
or-program
scm> (eval or-program)
hello
scm> (eval (make-long-or '((= 1 0) #f (+ 1 2) (print 'goodbye))))
3
scm> (eval (make-long-or '((> 3 1))))
#t
scm> (eval (make-long-or '()))
#fRegex
Q8: Phone Number Validator
Create a regular expression that matches phone numbers that are 11, 10, or 7 numbers long.
Phone numbers 7 numbers long have a group of 3 numbers followed by a group of 4 numbers, either separated by a space, a dash, or nothing.
Examples: 123-4567, 1234567, 123 4567
Phone numbers 10 numbers long have a group of 3 numbers followed by a group of 3 numbers followed by a group of 4 numbers, either separated by a space, a dash, or nothing.
Examples: 123-456-7890, 1234567890, 123 456 7890
Phone numbers 11 numbers long have a group of 1 number followed by a group 3 numbers followed by a group of 3 numbers followed by a group of 4 numbers, either separated by a space, a dash, or nothing.
Examples: 1-123-456-7890, 11234567890, 1 123 456 7890
It is fine if spacing/dashes/no space mix! So 123 456-7890 is fine.
Note: The skeleton code is just a suggestion; feel free to use your own structure if you prefer.
Run in 61A CodeBNF
Q9: Comprehension is Everything
(Adapted from Spring 2021 Final) The following EBNF grammar can describe a subset of Python list comprehensions, but cannot yet describe all of them.
start: comp
?comp: "[" expression "for" IDENTIFIER "in" IDENTIFIER "]"
expression: IDENTIFIER operation*
operation: OPERATOR NUMBER
IDENTIFIER: /[a-zA-Z]+/
OPERATOR: "*" | "/" | "+" | "-"
%import common.NUMBER
%ignore /\s+/Select all of the non-terminal symbols in the grammar:
compexpressionoperationNUMBERIDENTIFIEROPERATOR
Which of the following comprehensions would be successfully parsed by the grammar?
[x * 2 for x in list][x for x in list][x ** 2 for x in list][x + 2 for x in list if x == 1][x * y for x in list for y in list2][x - 2 for x in my_list][x - y for (x,y) in tuples]
Recall that we can provide an optional if clause to the list comprehension which filters the resulting list based on the given condition. For example, an expression like [x - 3 for x in list if x > 7] is possible. Which line(s) would we need to modify to add support for the syntax described above, assuming that the conditional always compares an expression to a number?
OPERATOR: "*" | "/" | "+" | "-"IDENTIFIER: /[a-zA-z]+/operation: OPERATOR NUMBERexpression: IDENTIFIER operation*?comp: "[" expression "for" IDENTIFIER "in" IDENTIFIER "]"
Now modify the selected line(s) so that it can parse the syntax described above.
We can also nest list comprehensions within list comprehensions. For example, [[z * 2 for z in list] for x in [y + 1 for y in list2]] is valid Python syntax. As we can see, the nested list comprehension can go into either the map expression or the iterable expression or both. Modify the grammar so that it can now parse nested list comprehensions.